GNN|如何做的比卷积神经网络更好?
点击上方“小白学视觉”,选择加"星标"或“置顶”
重磅干货,第一时间送达


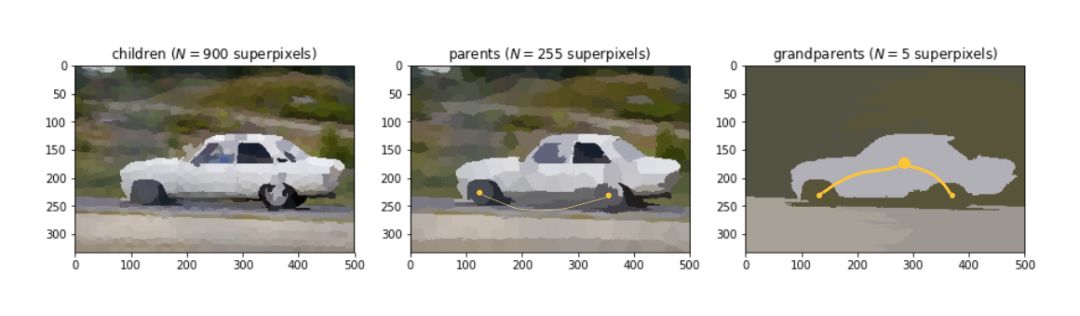
1. 层次图
def compute_iou_binary(seg1, seg2):
inters = float(np.count_nonzero(seg1 & seg2))
#区域可以预先计算
seg1_area = float(np.count_nonzero(seg1))
seg2_area = float(np.count_nonzero(seg2))
return inters / (seg1_area + seg2_area - inters)
def hierarchical_graph(masks_multiscale, n_sp_actual, knn_graph=32):
n_sp_total = np.sum(n_sp_actual)
A = np.zeros((n_sp_total, n_sp_total))
for level1, masks1 in enumerate(masks_multiscale):
for level2, masks2 in enumerate(masks_multiscale[level1+1:]):
for i, mask1 in enumerate(masks1):
for j, mask2 in enumerate(masks2):
A[np.sum(n_sp_actual[:level1], dtype=np.int) + i,
np.sum(n_sp_actual[:level2+level1+1], dtype=np.int) + j] = compute_iou_binary(mask1, mask2)
sparsify_graph(A, knn_graph)
return A + A.T
n_sp_actual = []
avg_values_multiscale, coord_multiscale, masks_multiscale = [], [], []
# Scales [1000, 300, 150, 75, 21, 7] ]在论文中
for i, (name, sp) in enumerate(zip(['children', 'parents', 'grandparents'], [1000, 300, 21])):
superpixels = slic(img, n_segments=sp)
n_sp_actual.append(len(np.unique(superpixels)))
avg_values_, coord_, masks_ = superpixel_features(img, superpixels)
avg_values_multiscale.append(avg_values_)
coord_multiscale.append(coord_)
masks_multiscale.append(masks_)
A_spatial_multiscale = spatial_graph(np.concatenate(coord_multiscale), img.shape[:2], knn_graph=knn_graph)
A_hier = hierarchical_graph(masks_multiscale, n_sp_actual, knn_graph=None)
到目前为止,如果我们可视化滤波器,它们将看起来非常原始(就像高斯一样)。有关更多详细信息,请参见我的[GNN教程](https://medium.com/@BorisAKnyazev/tutorial-on-graph-neural-networks-for-computer-vision-and-beyond-part-1-3d9fada3b80d)。我们想学习一些类似于ConvNets的边缘检测器,因为效果很好。但是事实证明,使用GNN来学习它们非常困难。为此,我们基本上需要根据坐标之间的差异在超像素之间生成边缘。这样,我们将使GNN能够理解坐标系(旋转,平移)。我们将使用在PyTorch中定义的2层神经网络,如下所示:
pred_edge = nn.Sequential(nn.Linear(2, 32),
nn.ReLU(True),
nn.Linear(32, L))
其中L是预测边数或滤波器数,例如下面的图表中的4。
我们限制滤波器仅根据 |(x₁,y₁) - (x₂,y₂)|之间的绝对差而不是原始值来学习边缘,从而使滤波器变得对称。 这限制了滤波器的容量,但是它仍然比我们的基准GCN使用的简单高斯滤波器好得多。
在我的[Jupyter笔记本](https://github.com/bknyaz/bmvc_2019/blob/master/bmvc_2019.ipynb)中,我创建了一个LearnableGraph类,该类实现了在给定节点坐标(或任何其他特征)和空间图的情况下预测边缘的逻辑。 后者用于在每个节点周围定义一个小的局部邻域,以避免预测所有可能的节点对的边缘,因为它昂贵且连接非常远的超像素没有多大意义。
下面,我将训练有素的pred_edge函数可视化。 为此,我假设在其中应用卷积的索引为1的当前节点位于坐标系(x₁,y₁)= 0的中心。 然后,我简单地采样其他节点的坐标(x₂,y₂),并将其输入给pred_edge。 颜色显示边缘的强度取决于与中心节点的距离。

学习到的图也非常强大,但是计算量较大,如果我们生成非常稀疏的图,则可以忽略不计。32.3%的结果仅比ConvNet低0.4%,如果我们生成更多的过滤器,则可以轻松地改善它!
现在,我们有了三个图:空间图,层次图和学习图。 具有空间或层次图的单个图卷积层仅允许特征在“第一邻居”内传播。 在我们的例子中,邻居是软性定义的,因为我们使用高斯来定义层次图的空间图和IoU。 (Defferrard等。 NIPS(2016))提出了一种多尺度(multihop)图卷积算法,该算法将K-hop邻域内的特征聚合在一起并近似谱图卷积。 有关此方法的详细说明,请参见我的[其他文章](https://towardsdatascience.com/tutorial-on-graph-neural-networks-for-computer-vision-and-beyond-part-2-be6d71d70f49)。 对于我们的空间图,它实质上对应于使用多个不同宽度的高斯。 对于分层图,我们可以通过这种方式在远程子节点之间创建K-hop快捷方式。 对于学习的图,此方法将创建可视化的学习过滤器的多个比例。
使用多尺度图卷积,在我的GraphLayerMultiscale类中实现,结果证明是非常重要的,它使我们的性能比基准卷积神经网络高出0.3%!
到目前为止,为了从我们的三个图中学习,我们使用了标准的级联方法。 但是,这种方法有两个问题。 首先,这种融合算子的可训练参数的数量是线性的。 输入和输出要素的维数,比例(K)和关系类型的数量,因此,如果我们一次增加两个或多个这些参数,它的确会快速增长。 其次,我们尝试融合的关系类型可以具有非常不同的性质,并占据流形的非常不同的子空间。 为了同时解决这两个问题,我们提出了类似于(Knyazev等人,NeurIPS-W,2018)的可学习的预测。 通过这种方式,我们将线性相关性解耦,与串联相比,参数数量减少了2-3倍。 此外,可学习的投影变换了多关系特征,因此它们应占据流形的附近子空间,从而促进信息从一种关系传播到另一种关系。
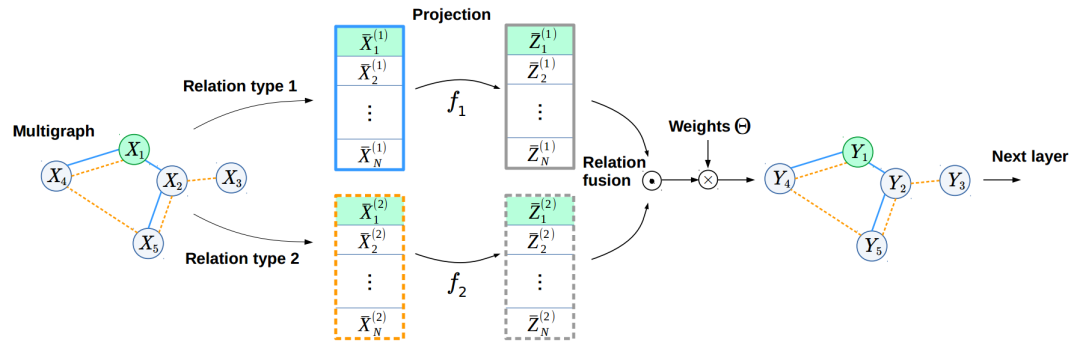
通过使用在下面的GraphLayerFusion类中实现的拟议融合方法,我们将ConvNet击败了达到了34.5%提升1.8%,而参数却减少了2倍! 对于最初对图像的空间结构一无所知的模型,除了以超像素编码的信息外,还给人留下了深刻的印象。 探索其他融合方法(例如这种方法)以获得更好的结果将很有趣。
class GraphLayerFusion(GraphLayerMultiscale):
def __init__(self,
in_features,
out_features,
K,
fusion='pc',
n_hidden=64,
bnorm=True,
activation=nn.ReLU(True),
n_relations=1):
super(GraphLayerFusion, self).__init__(in_features, out_features, K, bnorm, activation, n_relations)
self.fusion = fusion
if self.fusion == 'cp':
fc = [nn.Linear(in_features * K * n_relations, n_hidden),
nn.ReLU(True),
nn.Linear(n_hidden, out_features)]
else:
if self.fusion == 'pc':
fc = [nn.Linear(n_hidden * n_relations, out_features)]
elif self.fusion == 'sum':
fc = [nn.Linear(n_hidden, out_features)]
else:
raise NotImplementedError('cp, pc or sum is expected. Use GraphLayer for the baseline concatenation fusion')
self.proj = nn.ModuleList([nn.Sequential(nn.Linear(in_features * K, n_hidden), nn.Tanh())
for rel in range(n_relations)]) # projection layers followed by nonlinearity
if bnorm:
fc.append(BatchNorm1d_GNN(out_features))
if activation is not None:
fc.append(activation)
self.fc = nn.Sequential(*fc)
def relation_fusion(self, x, A):
B, N = x.shape[:2]
for rel in range(self.n_relations):
y = self.chebyshev_basis(A[:, :, :, rel], x, self.K).view(B, N, -1) # B,N,K,C
if self.fusion in ['pc', 'sum']:
y = self.proj[rel](y) # projection
if self.fusion == 'sum':
y_out = y if rel == 0 else y_out + y
continue
# for CP and PC
if rel == 0:
y_out = []
y_out.append(y)
y = self.fc(y_out if self.fusion == 'sum' else (torch.cat(y_out, 2))) # B,N,F
return y
事实证明,有了多关系图网络和一些技巧,我们可以比卷积神经网络做得更好!
不幸的是,在改进GNN的过程中,我们逐渐失去了不变性。例如,旋转图像后,超像素的形状可能会发生变化,而我们用于节点特征以改善模型的超像素坐标也使其健壮性降低。
尽管如此,我们的工作只是迈向更好的图像推理模型的一小步,并且我们证明了GNN可以为一个有希望的方向铺平道路。
有关实现的详细信息,请参阅我在Github上的[笔记本](https://github.com/bknyaz/bmvc_2019)。
我还高度推荐Matthias Fey的硕士论文,其中包含与非常相关的主题相关的[代码](https://github.com/rusty1s/embedded_gcnn)。
交流群
欢迎加入公众号读者群一起和同行交流,目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群(以后会逐渐细分),请扫描下面微信号加群,备注:”昵称+学校/公司+研究方向“,例如:”张三 + 上海交大 + 视觉SLAM“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告,否则会请出群,谢谢理解~
