机器学习中，大部分是分类问题，另一种常见的机器学习问题是回归问题，它预测一个连续值而不是离散的标签，例如，根据气象数据预测明天的气温，或者根据软件说明书预测完成软件项目所需要的时间、根据消费行为预测用户的年龄等，今天的案例就是根据周边的数据，预测房价，房价是一系列的连续值，因此是一个典型的回归问题。

注意：不要将回归问题与 logistic 回归算法混为一谈。令人困惑的是，logistic 回归不是回归算法， 而是分类算法。

一、波士顿房价数据集

本节将要预测 20 世纪 70 年代中期波士顿郊区房屋价格的中位数，已知当时郊区的一些数据点，比如犯罪率、当地房产税率等。本节用到的数据集与前面两个例子有一个有趣的区别。

它包含的数据点相对较少，只有 506 个，分为 404 个训练样本和 102 个测试样本。输入数据的 每个特征（比如犯罪率）都有不同的取值范围。例如，有些特性是比例，取值范围为 0~1；有 的取值范围为 1~12；还有的取值范围为 0~100，等等。

加载波士顿房价数据

from keras.datasets import boston_housing(train_data,train_targets),(test_data,test_targets) = boston_housing.load_data()

我们来看一下数据。

train_data.shape (404, 13) test_data.shape (102, 13)

如你所见，我们有 404 个训练样本和 102 个测试样本，每个样本都有 13 个数值特征，比如人均犯罪率、每个住宅的平均房间数、高速公路可达性等。目标是房屋价格的中位数，单位是千美元。

train_targetsarray([15.2, 42.3, 50. , 21.1, 17.7, 18.5, 11.3, 15.6, 15.6, 14.4, 12.1,17.9, 23.1, ......

房价大都在 10 000~50 000 美元。折合人民币6.5w-40w一平米，如果你觉得这很便宜，不要忘记当时是 20 世纪70年代中期，而且这些价格没有根据通货膨胀进行调整。所以一线城市的房价，还大有上涨空间

二、准备数据

将取值范围差异很大的数据输入到神经网络中，这是有问题的。网络可能会自动适应这种取值范围不同的数据，但学习肯定变得更加困难。对于这种数据，普遍采用的最佳实践是对每个特征做标准化，即对于输入数据的每个特征（输入数据矩阵中的列），减去特征平均值，再除 以标准差，这样得到的特征平均值为 0，标准差为 1。用 Numpy 可以很容易实现标准化。

# 数据归一化mean = train_data.mean(axis = 0)train_data -= meanstd = train_data.std(axis = 0)train_data /= stdtest_data -= meantest_data /= std

 注意：用于测试数据标准化的均值和标准差都是在训练数据上计算得到的。在工作流程中，你不能使用在测试数据上计算得到的任何结果，即使是像数据标准化这么简单的事情也不行。

三、构建模型框架

由于样本数量很少，我们将使用一个非常小的网络，其中包含两个隐藏层，每层有 64 个单元。一般来说，训练数据越少，过拟合会越严重，而较小的网络可以降低过拟合。

#构建模型框架from keras import layers from keras import modelsdef build_model():    model = models.Sequential()    model.add(layers.Dense(64,activation='relu',input_shape=(train_data.shape[1],)))    model.add(layers.Dense(64,activation='relu'))    model.add(layers.Dense(1))    model.compile(optimizer='rmsprop',loss='mse',metrics=['mae'])    return model

网络的最后一层只有一个单元，没有激活，是一个线性层。这是标量回归（标量回归是预测单一连续值的回归）的典型设置。添加激活函数将会限制输出范围。例如，如果向最后一层添加 sigmoid 激活函数，网络只能学会预测 0~1 范围内的值。这里最后一层是纯线性的，所以 网络可以学会预测任意范围内的值。

注意，编译网络用的是 mse 损失函数，即均方误差（MSE，mean squared error），预测值与 目标值之差的平方。这是回归问题常用的损失函数。

在训练过程中还监控一个新指标：平均绝对误差（MAE，mean absolute error）。它是预测值 与目标值之差的绝对值。比如，如果这个问题的 MAE 等于 0.5，就表示你预测的房价与实际价格平均相差 500 美元。

四、利用K 折验证来验证你的方法

为了在调节网络参数（比如训练的轮数）的同时对网络进行评估，你可以将数据划分为训练集和验证集，正如前面例子中所做的那样。但由于数据点很少，验证集会非常小（比如大约100 个样本）。因此，验证分数可能会有很大波动，这取决于你所选择的验证集和训练集。也就是说，验证集的划分方式可能会造成验证分数上有很大的方差，这样就无法对模型进行可靠的评估。

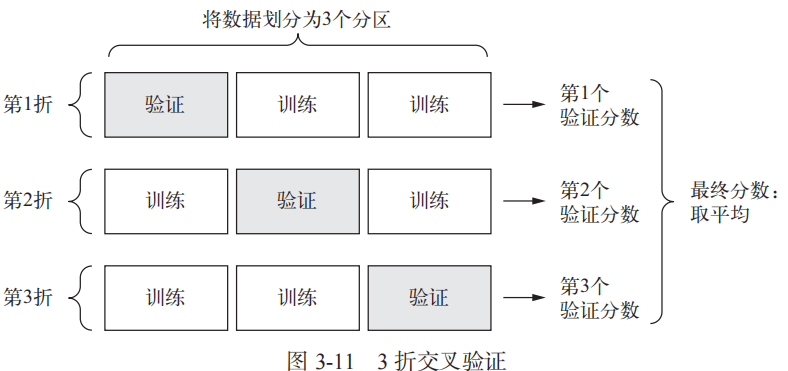
在这种情况下，最佳做法是使用 K 折交叉验证（见图 3-11）。这种方法将可用数据划分为 K个分区（K 通常取 4 或 5），实例化 K 个相同的模型，将每个模型在 K-1 个分区上训练，并在剩下的一个分区上进行评估。模型的验证分数等于 K 个验证分数的平均值。这种方法的代码实现很简单。

import keras import numpy as np #K折交叉验证k   = 5num = len(train_data)//kall_score = []for i in range(k):    X_val = train_data[i*num:(i+1)*num]    Y_val = train_targets[i*num:(i+1)*num]    X_train = np.concatenate([train_data[:i*num],train_data[(i+1)*num:]],axis=0)    Y_train = np.concatenate([train_targets[:i*num],train_targets[(i+1)*num:]],axis=0)    model = build_model()    model.fit(X_train,Y_train,epochs=100,batch_size=1,verbose=1)    val_mse,val_mae = model.evaluate(X_val,Y_val,verbose=0)    all_score.append(val_mae)

运行结果如下，取平均，基本上就是模型能到达的最小误差了

all_score[1.9652233123779297,2.5989739894866943,1.9110896587371826,2.5641400814056396, 2.337777853012085]
np.mean(all_score) 2.275440979003906

每次运行模型得到的验证分数有很大差异，从 1.9 到 2.6 不等。平均分数（2.27）是比单一分数更可靠的指标——这就是 K 折交叉验证的关键。在这个例子中，预测的房价与实际价格平均相差 2200 美元，考虑到实际价格范围在 10 000~50 000 美元，这一差别还是很大的。我们让训练时间更长一点，达到 500 个轮次。为了记录模型在每轮的表现，我们需要修改训练循环，以保存每轮的验证分数记录。

五、模型最后评估

完成模型调参之后（除了轮数，还可以调节隐藏层大小），你可以使用最佳参数在所有训练数据上训练最终的生产模型，然后观察模型在测试集上的性能。

model = build_model()model.fit(train_data,train_targets,epochs=100,batch_size=1,verbose=1)test_mse,test_mae = model.evaluate(test_data,test_targets,verbose=0)
test_mae2.213838815689087
#如果要看预测的明细结果model.predict(test_data)array([[18.471083],       [20.257647],       [33.627922],       [23.181114],       [23.600664],       [29.277847],       [21.298449],       [17.50559 ],       [21.228243]], dtype=float32)

从上述结果来看，交叉验证的结果与最后的预测结果相差不大，因此要得到更准的线上精度，最好选择交叉验证，而不是一次性的分割验证。

···  END  ···