梳理 | 交叉熵、相对熵(KL散度)、JS散度和Wasserstein距离(推土机距离)
作者 KevinCK 编辑 极市平台 侵删
来源 https://zhuanlan.zhihu.com/p/74075915
目录:
信息量
熵
相对熵(KL散度)
交叉熵
JS散度
推土机理论
Wasserstein距离
WGAN中对JS散度,KL散度和推土机距离的描述
写在前面的总结
目前分类损失函数为何多用交叉熵,而不是 KL 散度。
首先损失函数的功能是通过样本来计算模型分布与目标分布间的差异,在分布差异计算中,KL 散度是最合适的。但在实际中,某一事件的标签是已知不变的(例如我们设置猫的 label 为 1,那么所有关于猫的样本都要标记为 1),即目标分布的熵为常数。而根据下面 KL 公式可以看到,KL 散度 - 目标分布熵 = 交叉熵(这里的“-”表示裁剪)。所以我们不用计算 KL 散度,只需要计算交叉熵就可以得到模型分布与目标分布的损失值。
从上面介绍,知道了模型分布与目标分布差异可用交叉熵代替 KL 散度的条件是目标分布为常数。如果目标分布是有变化的(如同为猫的样本,不同的样本,其值也会有差异),那么就不能使用交叉熵,例如蒸馏模型的损失函数就是 KL 散度,因为蒸馏模型的目标分布也是一个模型,该模型针对同类别的不同样本,会给出不同的预测值(如两张猫的图片 a 和 b,目标模型对 a 预测为猫的值是 0.6,对 b 预测为猫的值是 0.8)。
注:交叉熵和 KL 散度应用方式不同的另一种解释(我更倾向于上面我自己的解释,更具公式解释性):
交叉熵:其用来衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。这也是为什么在机器学习中的分类算法中,我们总是最小化交叉熵,因为交叉熵越低,就证明由算法所产生的策略最接近最优策略,也间接证明我们算法所算出的非真实分布越接近真实分布。
KL 散度(相对熵):衡量不同策略之间的差异呢,所以我们使用 KL 散度来做模型分布的拟合损失。
详细内容
信息量:
任何事件都会承载着一定的信息量,包括已经发生的事件和未发生的事件,只是它们承载的信息量会有所不同。如昨天下雨这个已知事件,因为已经发生,既定事实,那么它的信息量就为 0。如明天会下雨这个事件,因为未有发生,那么这个事件的信息量就大。
从上面例子可以看出信息量是一个与事件发生概率相关的概念,而且可以得出,事件发生的概率越小,其信息量越大。这也很好理解,狗咬人不算信息,人咬狗才叫信息嘛。
我们已知某个事件的信息量是与它发生的概率有关,那我们可以通过如下公式计算信息量:
熵:
相对熵(KL 散度):

KL 散度不是对称的; KL 散度不满足三角不等式。
交叉熵:

JS 散度:
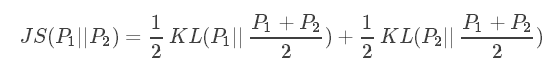
Wasserstein 距离(该部分摘自KL 散度、JS 散度、Wasserstein 距离):
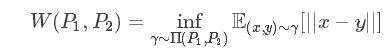
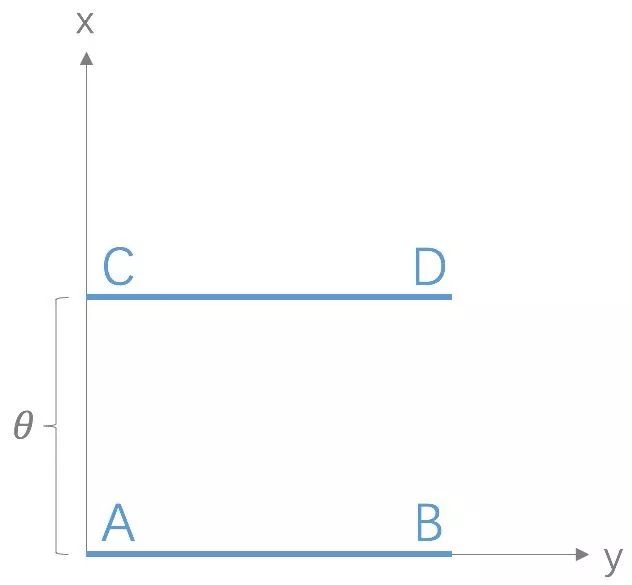
WGAN中对KL散度和JS散度的描述(摘自:郑华滨:令人拍案叫绝的Wasserstein GAN)
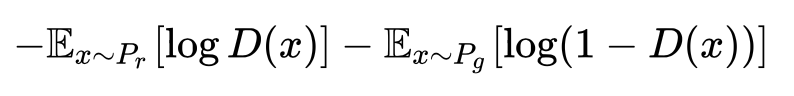






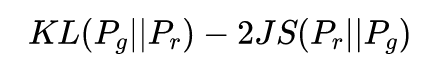
参考:
1、https://blog.csdn.net/tsyccnh/article/details/79163834
2、[论文笔记] 损失函数整理(https://zhuanlan.zhihu.com/p/35027284)
猜您喜欢:
附下载 |《TensorFlow 2.0 深度学习算法实战》
