Python算法-分块查找算法


图19 书口索引块
分块查找就是把一个大的线性表分解成若干块,每块中的节点可以任意存放,但块与块之间必须排序。与此同时,还要建立一个索引表,把每块中的最大值作为索引表的索引值,此索引表需要按块的顺序存放到一个辅助数组中。查找时,首先在索引表中进行查找,确定要找的结点所在的块。由于索引表是排序的,因此,对索引表的查找可以采用顺序查找或二分查找;然后,在相应的块中采用顺序查找,即可找到对应的结点。 例如,有这样一列数据:23、43、56、78、97、100、120、135、147、150。如图20所示。 
图20 数据
想要查找的数据是150,使用分块查找法步骤如下: 步骤1:将图16所示的数据进行分块,按照每块长度为4进行分块,分块情况如图21所示。 说明:每块的长度是任意指定的,笔者在这里用的长度为4,读者可以根据自己的需要指定每块长度。 
图21 对数据进行分块
步骤2:选取各块中的最大关键字构成一个索引表,即选取图18所示的各块的最大值,第一块最大的值是78,第二块最大的值是135,第三块最大值是155形成的索引表如图22所示。 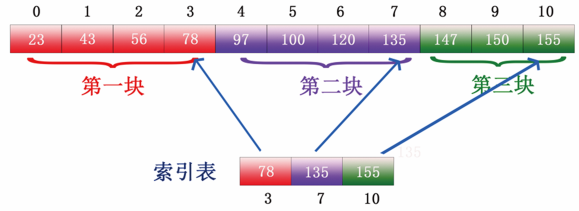
图22 索引表
步骤3:用顺序查找或者二分查找判断想要查找数据150在图18所示的索引表中的哪块内容中,这里笔者用的是二分查找法,即先取中间值135与150比较,如图23所示。 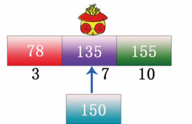
图23 中间值与目标值比较
步骤4:图19的结果是中间位置的数据135比目标数据150小,因此目标数据在135的下一块内。将数据定位在第3块内,此时将第3块内的数据取出,进行顺序比较,如图24所示。 
图24 顺序查找
步骤5:通过顺序查找第3块的内容,终于在第9个位置找到目标数,此时分块查找结束。 至此,分块查找算法已经讲解完毕。通过和二分查找法和顺序查找法对比来看,分块查找的速度虽然不如二分查找算法,但比顺序查找算法快得多。当数据很多且块数很大时,对索引表可以采用二分查找,这样能够进一步提高查找的速度。 接下来用Python代码来实现以上描述的分块查找。 实例5 实现分块查找算法 具体代码如下:def search(data, key): # 用二分查找 想要查找的数据在哪块内
length = len(data) # 数据列表长度
first = 0 # 第一位数位置
last = length – 1 # 最后一个数据位置
print("长度:%s 分块的数据是:%s"%(length,data)) # 输出分块情况
while first <= last:
mid = (last + first) // 2 # 取中间位置
if data[mid] > key: # 中间数据大于想要查的数据
last = mid - 1 # 将last的位置移到中间位置的前一位
elif data[mid] < key: # 中间数据小于想要查的数据
first = mid + 1 # 将first的位置移到中间位置的后一位
else:
return mid # 返回中间位置
return False
# 分块查找
def block(data, count, key): # 分块查找数据,data是列表,count是每块的长度,key是想要查找的数据
length = len(data) # 表示数据列表的长度
blockLength = length//count # 一共分的几块
if count * blockLength != length: # 每块长度乘以分块总数不等于数据总长度
blockLength += 1 # 块数加1
print("一共分", blockLength,"块") # 块的多少
print("分块情况如下:")
for block_i in range(blockLength): # 遍历每块数据
blockData = [] # 每块数据初始化
for i in range(count): # 遍历每块数据的位置
if block_i*count + i >= length: # 每块长度要与数据长度比较,一旦大于数据长度
break # 就退出循环
blockData.append(data[block_i*count + i] )# 每块长度要累加上一块的长度
result = search(blockData, key) # 调用二分查找的值
if result != False: # 查找的结果不为False
return block_i*count + result # 就返回块中的索引位置
return False
data = [23,43,56,78,97,100,120,135,147,150,155] # 数据列表
result = block(data, 4, 150) # 第二个参数是块的长度,最后一个参数是要查找的元素
print("查找的值得索引位置是:", result) # 输出结果
运行结果如图25所示。
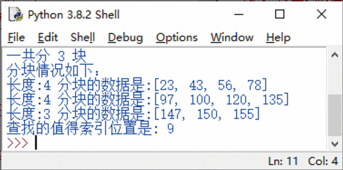
图25 分块查找结果
从3.21中的运行结果看到,当查找150时,查找结果完全符合上述描述的步骤。

评论
