二分查找算法（下）：通过 LeetCode 周赛学习二分查找算法

重磅干货，第一时间送达

一个二分查找算法和贪心算法结合的场景

之所以写这个，是因为我前两周在参加 LeetCode 周赛的时候，碰到了一个这样题，点击「阅读原文」可以直达题目链接，题目具体如下：

1648. 销售价值减少的颜色球

你有一些球的库存 inventory ，里面包含着不同颜色的球。一个顾客想要 任意颜色 总数为 orders 的球。

这位顾客有一种特殊的方式衡量球的价值：每个球的价值是目前剩下的 同色球 的数目。比方说还剩下 6 个黄球，那么顾客买第一个黄球的时候该黄球的价值为 6 。这笔交易以后，只剩下 5 个黄球了，所以下一个黄球的价值为 5 （也就是球的价值随着顾客购买同色球是递减的）。

给你整数数组 inventory ，其中 inventory[i] 表示第 i 种颜色球一开始的数目。同时给你整数 orders ，表示顾客总共想买的球数目。你可以按照 任意顺序 卖球。

请你返回卖了 orders 个球以后 最大 总价值之和。由于答案可能会很大，请你返回答案对 10 ** 9 + 7 取余数 的结果。

示例 1：

输入：inventory = [2,5], orders = 4

输出：14

解释：卖 1 个第一种颜色的球（价值为 2 )，卖 3 个第二种颜色的球（价值为 5 + 4 + 3）。

最大总和为 2 + 5 + 4 + 3 = 14 。

提示

• 1 <= inventory.length <= 10 ** 5

• 1 <= inventory[i] <= 10 ** 9

• 1 <= orders <= min(sum(inventory[i]), 10 ** 9)

分析

刚开始我完全没有意识到有二分查找的思想，就是想着用一个优先队列，然后每次取出一个元素，加上当前值，把当前值减一，然后再把当前值放入优先队列。

没过几分钟，程序就写完了，但是呢提交后显示运行超时了，我就想着去优化程序。于是我又读了下题，看看是不是我漏了啥重要条件，结果读了几遍发现这道题就是贪心的思想啊，不可能错的呀，但是结果就是超时了。。。

于是周赛结束后我特意去查了下大神写的代码，真的是让我惊呆了，是贪心的思想没错，但是是二分和贪心进行结合。

这个题想法很简单，设置一个 sum 变量，sum 每次加上数组中的最大值，然后将当前值减去 1，直到此过程重复 orders 步骤。

然后为啥用优先队列会超时呢？其实优先队列的底层就是堆，每次取出元素，加入元素都需要对堆进行调整，调整的时间复杂度是 O(logn),其中 n 是优先队列的长度，然后需要进行 orders 操作，所以总的时间复杂度就是 O(Nlogn), 其中 N 是 orders， n 是数组长度。

而这道题的话，orders 会取到 10 ** 9,所以自然而然就会超时了。

那么应该如何解决呢？

解决思路

既然单独使用优先队列解决不了问题，那我们就换个思路进行思考。因为每次都要取数组中的最大值，然后减去 1, 所以最后呢数组中的元素肯定是小于等于某一个阈值的，这个我想你肯定是能够理解的。

那这个阈值能不能求出来呢？如果能求出来的话，那问题是不是就容易解决了呢？你想啊，如果现在我们已经求出了这个阈值，那么是不是就知道了数组中的每个元素被减了多少次，进而累加求和不就得到结果了嘛。

好，现在问题已经变成了如何求解阈值了，这个如何求解呢？我们假定阈值为 threshold,那么它满足啥条件呢？

怎么理解呢？

就是说当前值是 threshold时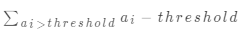， 就代表了所有的操作的次数，它应该是小于等于 orders的，为啥呢？拿例 1 举例，数组为 [2, 5], orders 为 4,相当于要进行四次操作。

1. 5 减 1,变为 4

2. 4 减 1,变为 3

3. 3 减 1,变为 2

4. 剩下两个 2, 2 减 1,变为 1

此时所有数组中的元素都小于等于 2,所以这个例子中的 threshold就是 2。但是有可能出现小于 orders 的情况，比如文中的这个例子，这时候又需要当前数组中的部分元素再减去 1,但是又不能所有元素都减去 1,如果那样的话， threshold 就会改变了。

因为这个函数是一个单调递减的函数，所以存在唯一的 threshold,满足上述式子。所以问题就转化为了在 0 和 10 ** 9 之间查找最小的 threshold,使得

看到了吗？这个问题就转化为了上篇文章中我们提到的二分算法的变体问题，没理解的话，你品，你再品。

然后就表示了数组中元素还需要再减 1 的次数。

这个问题到这里就解决了，接下来看看代码吧，这里面还有很多骚操作，保证出乎你的意外。

代码实现

 1class Solution:
 2    def maxProfit(self, inventory: List[int], orders: int) -> int:
 3        max_num = 10 ** 9 + 7
 4        res = 0
 5        low, high = 0, 10 ** 9
 6        threshold = None
 7        while low <= high:
 8            mid = low + ((high - low) >> 1)
 9            temp = 0
10            for i in range(len(inventory)):
11                if inventory[i] >= mid:
12                    temp += (inventory[i] - mid)
13            if temp <= orders:
14                threshold = mid
15                high = mid - 1
16            else:
17                low = mid + 1
18        temp = 0
19        for i in range(len(inventory)):
20            if inventory[i] > threshold:
21                temp += (inventory[i] - threshold)
22        temp = orders - temp
23        for i in range(len(inventory)):
24            if inventory[i] >= threshold:
25                if temp > 0:
26                    # 等差数列求和公式
27                    res += ((inventory[i] + threshold) * (inventory[i] - (threshold) + 1) // 2)
28                    temp -= 1
29                else:
30                    # 等差数列求和公式
31                    res += ((inventory[i] + threshold + 1) * (inventory[i] - (threshold + 1) + 1) // 2)
32        return res % max_num

这个是我今天下午刚写的，前一部分是二分查找的实现，后面是累加求和的过程。

不知道最后一个 for 循环你看懂了没？在计算 res的过程中，运用到了等差数列的求和公式，我当时在看别人代码的时候是一脸懵逼的，当时想着计算的话不是应该有循环的吗？为啥没有循环呢？没有循环怎么计算从 a[i] 到 threshold 呢？突然间恍然大悟，不得不佩服大神。

总结

现在回过头来看，这道题的思想已经很正常了，但是当我在参加 LeetCode 周赛的时候，当时心态都被它给搞崩了。。。

你看提到二分查找算法的话，我想每个人都知道，提及贪心算法，每个人也都有话可说，但是二者结合起来，就让很多人摸不着头脑了。

当然，这并不是说我们之前学的算法知识没有用，而是我们缺乏一种融会贯通的思维，在学习的过程中，要学会举一反三。

这道题带给我的不仅仅是知识点的融会贯通，更让我惊讶的是数学知识的使用，没有刻意的地方，一切是那么的自然。

我们每个人学数学的话也都学了好多年，但是更多的是用来考试，真正在编程过程的使用时是很少的。

虽然那次周赛我只做了一道题，但是感觉收获是很大的，开阔了眼界，拓展了思维。

如果你对编程也感兴趣的话，欢迎联系我，我们共同交流进步。

一个人可以走的很快，但一群人可以走的更远，共勉。