一文搞懂戴克斯特拉算法-dijkstra

大学学习数据结构那会，当时记得终于把 dijkstra 算法搞明白了，但是今天碰到的时候，大脑又是一片空白，于是我就又学习了下，把自己的理解写下来，希望你也可以通过本文搞懂 dijkstra 算法。

dijkstra 的起源

dijkstra 已经 62 岁了，是由荷兰计算机科学家艾兹赫尔·戴克斯特拉在 1956 年制造，并于 3 年后在期刊上发表，在 2001 年的采访中^[1]他说到：从鹿特丹到格罗宁根的最短路径是什么？实际上，这就是对于任意两座城市之间的最短路问题。解决这个问题实际上大概只花了我 20 分钟：一天早上，我和我的未婚妻在阿姆斯特丹购物，累了，我们便坐在咖啡馆的露台上喝咖啡，然后我就试了一下能否用一个算法解决最短路问题。正如我所说，这是一个 20 分钟的发现。不过实际上，我在 3 年后的 1959 年才把这个算法发表在论文上。即使现在来看这篇论文的可读性也非常高，这个算法之所以如此优雅，其中一个原因就是我没用笔纸就设计了它。后来我才知道，没用笔纸设计的优点之一是你不得不避免所有可避免的复杂问题。令我惊讶的是，这个算法最终成为我成名的基石之一。"

dijkstra 解决什么问题

主要解决带权图的最短路径问题，如果图中的顶点表示城市，而边上的权重表示城市间开车行经的距离，该算法可以用来找到两个城市之间的最短路径。dijkstra 算法使用类似广度优先搜索的方法解决赋权图的单源最短路径问题。

广度优先搜索，这个应该很形象，记得在算法实现的时候使用队列就可以了。赋权图也好理解，就是边上有权重值，可以理解为两点之间的距离，单源最短路径，就是一个已知的点到其他所有点的最短路径。

当然了，单源最短路径算法也不是只有 dijkstra，还有 Bellman-ford 算法或者 SPFA 算法，在边权非负时适合使用 Dijkstra 算法，若边权为负时则适合使用 Bellman-ford 算法或者 SPFA 算法。今天只聊 dijkstra。

dijkstra 算法思路

咱直接说优化后的思路，其实就是用到了小顶堆（优先级队列）来比较哪一个点的距离最近，关于堆排序，可以参考堆的实现及工程应用。

从起点 s 开始，将与起点 s 直接相连的点，根据它与起点 s 的距离，加入到小顶堆中，堆顶那个点 s1 与起点 s 的距离 d1 一定是最近的，取出堆顶的点 s1 ，然后把与 s1 直接相连的点，根据它与 s 的距离（d1 + s1到这个点的距离），加入到小顶堆中，堆顶那个点 s2 与起点的距离就是最小的。

每次取出堆顶元素的时候，这个堆顶就是已确认的最近距离的点，把它加入已访问的集合中，防止无向图的重复计算，这样直到遍历完所有顶点，就找出了起点到所有点的最小距离。

是不是很简单，就是广度搜索，加上贪心的思想，先找出起点 s 开始直接相连的点（广度搜索），然后找出与 s 第一个最近的点（贪心），从最近的点出发，再次广度，再次贪心，就可以找出距离起点 s 第二个最近的点，直到全部搜索完毕。

算法时间复杂度 O(E+Vlog(v)) ，E 是边的数量，V 是定点的数量，Vlog(v) 其实就是堆排序的时间复杂度。

算法时间复杂度 O(E+V) 邻接矩阵的空间复杂度。

如果还不理解的话，多看几遍下这个动图：

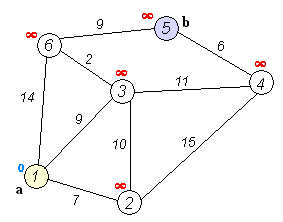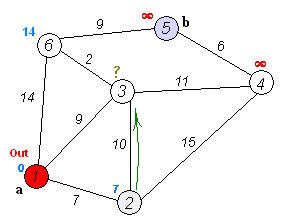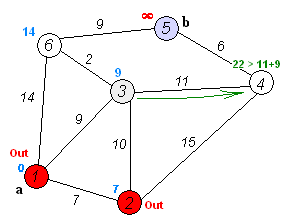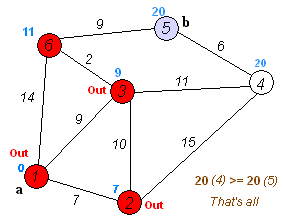
dijkstra 代码实现（Python）

为了简化说明，我们使用邻接矩阵来表示一个图，图中有 n 个顶点，标记为 1，2，...n，现在要求解起点 1 到所有其他点的最小距离。

以终为始，先定义一个保存结果的最小距离的数组，cost[n] cost[i] 就是表示起点 1 到点 i+1 的最小距离，cost[0] = 0，起点 1 到它本身的距离是 0。这里 i+1 是因为数组下标从 0 开始。

假如有 6 个顶点，使用邻接矩阵来表示：

adjacency_matrix = [
    [0,  7,  9,  -1, -1, 14],
    [7,  0,  10, 15, -1, -1],
    [9,  10, 0,  11, -1,  2],
    [-1, 15, 11, 0,  6,  -1],
    [-1, -1, -1, 6,  0,   9],
    [14, -1,  2, -1,  9,   0]
]

adjacency_matrix[i][j] = c 意思就是点 i+1 到 j+1 的成本是 c，加一的原因是数组的下标从 0 开始。

下面是我根据上述思路，实现的 dijkstra 算法，里面有注释，不难看懂：

import sys
import heapq

max = sys.maxsize

vertices_number = 6
adjacency_matrix = [
    [0, 7, 9, -1, -1, 14],
    [7, 0, 10, 15, -1, -1],
    [9, 10, 0, 11, -1, 2],
    [-1, 15, 11, 0, 6, -1],
    [-1, -1, -1, 6, 0, 9],
    [14, -1, 2, -1, 9, 0],
]

cost = [max] * vertices_number
pq = []  # 优先级队列，最小堆


class Node(object):
    def __init__(self, vertex, distance):
        self.vertex = vertex
        self.distance = distance

    def __lt__(self, other):
        """
        为了进堆时比较大小，重写 __lt__ 方法
        """
        return self.distance < other.distance


def printpq(pq):
    ## debug 用，查看堆里面的数据
    for item in pq:
        print(item.vertex, item.distance, end="|")
    print("")


def dijkstra(from_vertex, dest_vertex):
    from_vertex = from_vertex - 1  # 转换为列表的下标，因此减 1
    dest_vertex = dest_vertex - 1
    visited = set()  # 定义已经确定最小距离的点，防止重复计算。

    # 起点入队
    heapq.heappush(pq, Node(from_vertex, 0))  # 按照距离比较大小进堆
    while pq and len(visited) < vertices_number:
        # printpq(pq)
        # 出队
        node = heapq.heappop(pq)
        from_vertex1 = node.vertex
        distance1 = node.distance
        if from_vertex1 in visited:
            # 如果改点已经确认了最小距离，直接抛弃。
            continue
        # 更新距离，已经确定时最小距离的点加入已访问集合。
        print(from_vertex1)
        cost[from_vertex1] = distance1
        visited.add(from_vertex1)
        # 取出 from_vertex1 的邻居节点，
        for index, distance in enumerate(adjacency_matrix[from_vertex1]):
            # 只选择与 from_vertex1 连通的点，也就是邻居，排除已经确定了最小值的点。
            if distance > 0 and index not in visited:
                heapq.heappush(pq, Node(index, distance + distance1))

    return -1 if cost[dest_vertex] == max else cost[dest_vertex]


if __name__ == "__main__":
    print(dijkstra(1, 5))
    #其他点的最小距离均已经计算得出：
    print(cost)
    # assert 20 == dijkstra(1, 5)

最后的话

纯粹的记忆算法的实现其实没有太大用处，算法最重要的是理解它的思路，以及学会灵活的运用，比如说从 A 到 B 中间最多经过 k 个节点的最小距离，你可以试着用 dijkstra 算法的思路来求解么？假如有负数的权值，怎么用 dijkstra 算法求解？

如果有问题，请留言赐教。

都看到这里了，你不确定不关注一下吗？😄

参考资料