一文搞懂工程化协同推荐算法(三)

作者:livan
来源:数据EDTA
前言

经过前面两篇的文章:
一文搞懂工程化协同推荐算法(一)一文搞懂工程化协同推荐算法(二)
不知大家对推荐算法有没有一个系统的了解,推荐本身的逻辑很简单,就是需要找到用户喜欢的物品,然后呈现到用户的面前,这其实像是一个算法与用户的博弈,当用户到APP上的时候,留下一串足印,算法根据用户的足印和基本信息推断用户来这里想要做什么?或者说想要去什么地方?然后给他推荐他需要的东西。


推荐的基本结构基本上可以分成两类:
1) 基于协同理论的推荐算法:
如上文,协同理论就是找到相似的用户/物品或者相似的标签,然后根据交易历史中用户和物品的交互情况进行推荐。算法在进行过程中遇到各种问题,程序员用各种方法来解决这些问题,久而久之,延伸出了现在各种复杂的协同推荐模式。
常见的问题有:
1.1)人工进行特征工程的问题:1.2)运算量庞大的问题:1.3)特征挖掘层次不足的问题:1.4)如何使用社交链的问题:
2) 基于模型分类的推荐算法:
推荐从模型的角度理解可以看作是对用户喜好的预测,即为一个二分类的预测模型,根据用户的行为预测用户对某个商品喜欢不喜欢,进而根据喜好进行推荐。
基于模型的推荐比较多的应用于点击率预测,用户是否会购买某个商品的预测,在主流思路中依然是以协同为主。
下面我们延续上文的讨论,在上面常见问题的基础上深化我们对协同推荐的理解:

运算量庞大的问题

协同推荐的一个常见问题就是运算量的问题,每一次的迭代需要对全部的用户行为和商品信息进行复盘,计算出最新的相似系数。用户和商品量少的情况下还好说,可如果用户超过一亿,商品有上百万个呢?这一情况下UV矩阵就会非常大,每运算一次都需要耗费很大的资源,而且数据存在较多的稀疏的问题,几百万的商品,大部分用户点击的只有十几个,剩下的部分全都是零,极大的浪费运算资源。
所以,需要找寻一些方法来降低数据的运算,即常说的——降维。
一提到降维这个词,有没有很熟悉,对:很多人想到PCA、SVD等等常规的降维方法,在推荐算法中也有对应的基于降维的推荐方式:


——基于矩阵分解的系统推荐:
基于矩阵的推荐算法是以SVD奇异值分解为基础进行的。
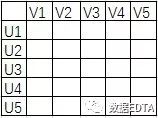
假设上图为用户的评分矩阵,经过上文的讲解,这个矩阵已经非常熟悉了吧,我们假设他现在有一亿行一亿列,那该如何降维呢?
我们在学习奇异值的时候,经常会听到一句话:前10%的奇异值之和占了全部奇异值之和的80%以上的比例。所以,我们只需要通过奇异值计算的方式找到前10%的奇异值k个,计算他对应的k个特征向量,即可大规模的降低上面UV矩阵的计算资源。
经过SVD的运算得到m*k的新的矩阵,我们就可以用这一矩阵替代UV矩阵进行相似度计算了。
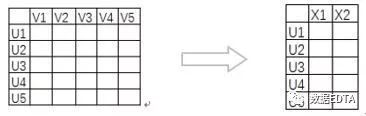
基于新的低阶矩阵我们计算出用户的相似度/物品相似度,然后再对相似用户进行推荐,计算效率大大的提升。
这样运算有两个好处:其一:减轻了线上存储和计算的压力;其二:解决了矩阵稀疏的问题;
也有一个坏处:
SVD是减轻了UV矩阵的运算量,但是SVD自身的运算呢?
从一个矩阵拆分成三个矩阵,这本身就意味着巨大的运算量,所以,在平时工作中很少使用SVD,而是使用隐语义模型,隐语义模型与SVD不同,他把矩阵拆分成了两个矩阵。


——ALS模式下隐语义推荐算法:
ALS是交替最小二乘法,主要是用来优化最小损失函数的。
即根据用户评分矩阵A,用求最小损失函数的方法求解出两个分解的参数矩阵:
K即为隐含的因子个数。对应的损失函数为:
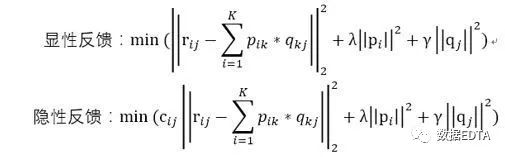
Cij即为用户偏爱某个商品的置信程度,交互次数多的权重就会增加。
这里,协同过滤就成功转化成了一个优化问题。通过ALS计算出用户因子矩阵P和物品因子矩阵Q。虽然降低了运算量,但是对于大数据集,还是推荐使用spark进行计算。
ALS模式的优点在于能够有效的解决过拟合的问题,同时对算法的可扩展性也有所提高。

特征挖掘层次不足的问题

虽然说矩阵分解的方法进行相似性计算已经非常成熟,但是,聪明的读者也已经发现,矩阵分解只是针对矩阵进行的一次运算,对特征的挖掘层次明显不足,而且,矩阵也没有用到用户和物品本身的特性。
而深度学习中的稀疏自编码模式可以有效的解决这两个问题:


——稀疏自编码模式下的推荐算法:
稀疏自编码是用神经网络的方式来压缩原始物品的特征向量,使物品的相似度运算能在较低纬度下进行。
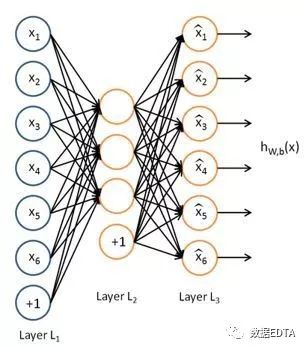
如图所示即为稀疏自编码的网络结构,简单来讲,稀疏自编码就是一个hw,b(x) = x的函数,设定神经网络的输入值和输出值都是x,中间多个隐含层的节点数量小于输入和输出层的节点数量(输入和输出层的节点数量一样多),对网络进行训练,输出层使用softmax进行训练,得到最后的隐含层为输出矩阵V,这一矩阵V即为经过稀疏自编码之后得到的物品的低维矩阵。
通常情况下,隐含层会有多层,以保证输入层的数据得到充分的运算,也就解决了上面讲的特征挖掘层次不足的情况,同时网络输入的是物品的属性信息,所以,第二个问题也得以解决。
假设一个物品的特性为v1=(x1,x2,x3,x4,x5,x6),经过上面的模型运算之后,向量就会变成v1=(k1, k2, k3)。
在使用稀疏自编码进行运算时有两个比较常用的延伸思路,是在使用稀疏自编码进行数据降维时频繁使用的方法,如下:
1) 添加随机因子:
如果直接将输入值看做输出层,有可能使输入层的数据直接穿透隐含层到达输出层,起不到准确训练的效果,此时可以在输入层中加入一些混淆因子,使输入和输出层不完全一致,即避免了数据穿透的问题。
随机因子应该是远远小于x的值,以保证搅乱一致性的同时不会引发x值变化。
2) 用已知的X、Y值:
在多层隐含层的自编码模式中有一种典型的方法是:栈式自编码。
即已知X和Y的值,通过输入X,输出Y训练多层隐含层,然后得到最后一个隐含层,作为X的压缩向量。
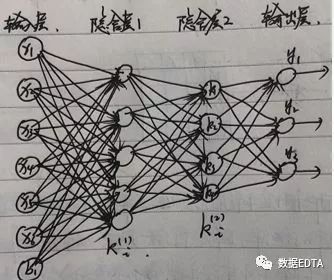
还是刚才的假设:v1=(x1,x2,x3,x4,x5,x6),输出层的标签为Y=(y1、y2、y3),经过两层隐含层的计算得到v1 = (k1, k2, k3, k4),这一特征向量涵盖了输入端的物品的用户评分属性和输出端的物品分类标签属性,是一个综合性的向量。基于这样的数据进行物品相似度计算能获得较好的效果。
写到这里,大家有没有发现,稀疏自编码并没有用上面的评分表,而是使用了基于内容的一些思路,推荐的协同逻辑发生了变化。所以,推荐本身不是基于一个固定不变的思路进行优化的,有时会不停的跳跃,直到找到较好的方法。

如何使用社交链的问题

不管什么样的APP都希望能够使用到社交网络的信息,因为社交网络本身就是一个计算良好的U-U矩阵,能够更准确的表示出用户的相似度。
社交网络主要有两种模式:兴趣图谱和社交图谱。
导致网络中会有三种常见的社交数据:1) 双向确认的社交数据,比如微信,A<——>B;2) 单向关注的社交数据,比如微博,A——>B;3) 基于社区的社交数据,比如知乎,A——>社区<——B;
在推荐算法中,社交网络最常用的用法还是与协同推荐结合使用,我们先看一个社交网络的图片:
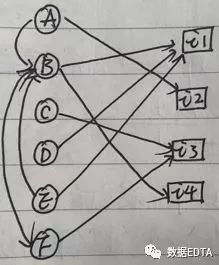
从图中可以看出,B有两人关注(A,E),有一人是好友(F),B购买了两个物品(i1,i4)。上图为社交网络的一个完整的图形,我们的推荐也是基于这一图形进行的。
限于篇幅,本文就写到这里~
下一篇文章我们来详细的讲解:基于社交网络的推荐方式和基于深度学习融合模型的推荐算法。

◆ ◆ ◆ ◆ ◆
长按二维码关注我们
数据森麟公众号的交流群已经建立,许多小伙伴已经加入其中,感谢大家的支持。大家可以在群里交流关于数据分析&数据挖掘的相关内容,还没有加入的小伙伴可以扫描下方管理员二维码,进群前一定要关注公众号奥,关注后让管理员帮忙拉进群,期待大家的加入。
管理员二维码:
评论
