贪心算法,一文搞懂

前言

今天学习一下贪心算法，从字面意思大概能体会到，这个算法的大致意思。

"贪心" 这个词大家都懂，就是总想要最好的，说明这个人比较贪嘛。贪心算法也属于五大常用算法之一。

基本概念

贪心算法是指，在对问题求解时，总是做出在当前看来，是最好的选择。也就是说，不从整体最优上加以考虑，它所做出的仅仅是在，某种意义上的局部最优解。

贪心算法注重，贪心策略的选择。必须注意的是，贪心算法不是对所有问题，都能得到整体最优解，选择的贪心策略必须具备无后效性。

即某个状态以后的过程不会影响以前的状态，只与当前状态有关。所以，对所采用的贪心策略一定要仔细分析其是否满足无后效性。

解题思路

下面看一下，使用贪心算法，解决问题的几个例子。

跳跃游戏

题目：
定一个非负整数数组，你最初位于数组的第一个位置。数组中的每个元素代表，你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个位置。

输入：  [2, 3, 1, 1, 4]

输出：true

解释: 我们可以先跳 1 步，从位置 0 到达 位置 1， 然后再从位置 1 跳 3 步，到达最后一个位置。

思路：贪心算法，每次找到可跳范围内的，数组值的最大值，看通过这个最大值，能否跳到尾部。不能跳到尾部，则遍历下一个，然后重复上述操作。

bool canJump(vector<int>& nums) {
   int n = nums.size();
   //最远可以到达的地方  
   int rightmost = 0;  

   //遍历数组
   for (int i = 0; i < n; ++i) {
      if (i <= rightmost) {
          //如果较大值可以到达，则说明可以到达
          rightmost = max(rightmost, i + nums[i]);
          if (rightmost >= n - 1) {
              return true;
          }
      }
   }
  return false;
}

会场安排问题

题目：
会场用来安排活动，每个活动，有一个开始时间和一个结束时间。在某个活动的开始时间，到结束时间这段范围内，其他活动不能再被安排，求最多能安排多少场活动。

#include<stdio.h>
#include<stdlib.h>
 
void GreedySelector(int n,int s[],int f[],int A[]){
    int i, j;
    //第一个活动要选，第一个结束时间最短,A[i]=1表示第i个活动入选
    A[1] = 1;
    //j=1表示取第一个活动的结束时间
    j = 1;
 
    //用i遍历每个活动
    for(i = 2; i <= n; i++){ 
        //这个活动的开始时间小于上个活动的结束时间
        if(s[i] > f[j]){
            A[i] = 1;
            j = i;
        } else {
            A[i] = 0;
        }
    }
}
 
int main(){
    int i;
    //每个活动按活动的结束时间进行排序
    //活动的开始时间
    int s[] = {0, 1, 3, 0, 5, 3, 5, 6, 8, 8, 2, 12};
    //活动的结束时间
    int f[] = {0, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}; 
    int n=11, A[11];
 
    GreedySelector(n, s, f, A);
    for(i = 1; i <= n; i++){
       if(A[i] == 1){
           printf("%d\n", i);
       }
    }
    return 0;
}

运行结果：1   4  8  11，这 4 个下标对应的活动。

策略选择：

• 开始时间最早优先（证明不可行）  

• 占用时间少优先(证明不可行)  

• 结束时间最早优先(使用贪心算法可以得到最优解)

加油站问题

题目：
一个汽车加满油后可以行使n千米，图中会经过一系列加油站，求到达最终加油的最少次数，给出每个加油站之间的距离。

#include<stdio.h>
//n表示汽车加满油后可以行使nkm
#define n 7 
 
int main()
{
     int a[n + 1] = {1, 2, 3, 4, 5, 1, 6, 6};
     //k表示途中有k个加油站 
     int k = 7;
     //油箱里的剩余油量，在起点时油量是满的
     int rest = 7;
     int count = 0;
     int i = 0;
 
     //n表示加满油可以行使n千米
     while(i < n + 1){
         //当前行程>rest
         if(a[i] > rest){
             //加油
             count ++;
             //重新赋值rest
             rest = n;
         }
  
         rest -= a[i];
         printf("rest=%d,i=%d\n", rest, i);
         i ++;
     }
 
    printf("the mininum is %d.", count);
    return 0;
}

每到一个加油站时，判断当前的油量，能否开到下一个加油站，再决定是否加油，i 表示对应的加油站。

贪心算法：局部最优能推导出整体最优，很容易，算法思维很常态化。

多次最优服务次序问题

问题描述：

设有n 个顾客同时等待一项服务。每个顾客需要服务一定时间。共有s 处可以

提供此项服务。

应如何安排n 个顾客的服务次序，才能使平均等待时间达到最小?平均等待时间是，n个顾客等待服务时间的总和除以n。

编程任务：

对于给定的，n个顾客需要的服务时间和s的值，编程计算最优服务次序。

#include<stdio.h>
#include<algorithm>
using namespace std;
 
//顾客数
#define n 10 
//服务窗口数  
#define s 2    

int main()
{
      //总共需要服务10位顾客，每位顾客需要服务的时间存在数组里
      int a[n] = {56, 12, 1, 99, 1000, 234, 33, 55, 99, 812};
      int i;
      int sum = 0;
 
      //服务窗口
      int sub[s] = {0};  
      sort(a, a + n);

      for(i = 0; i < n; i ++){
          sub[i % s] += a[i];
          sum += sub[i % s];
      }

      printf("%.2f", sum * 1.0 / n);
      return 0; 
} 

运行打印：336.00 

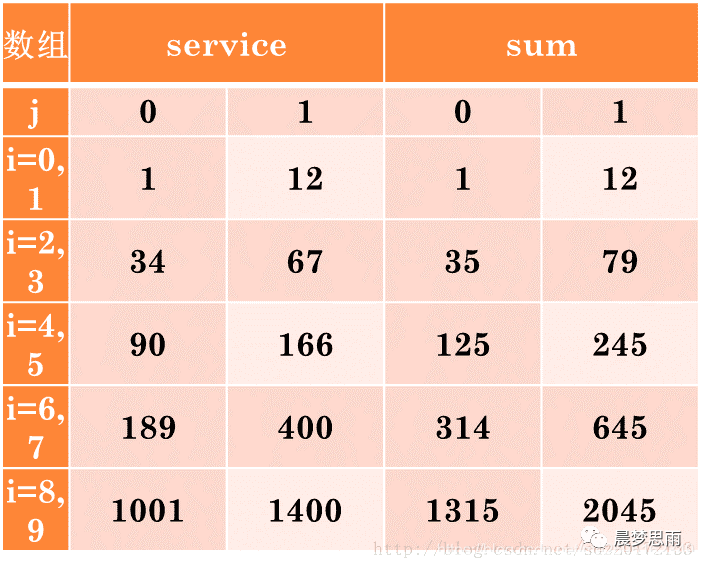
0 号窗口服务1，33，56....

1 号窗口服务12，55，99...

对应 0 号窗口，当服务 1 时，后面几位顾客需要等待的时间，就是前面几位顾客需要的服务时间的累加，前面有多少顾客就需要累加多少次。1 号窗口也是一样。

絮叨

·················· END ··················

点击关注公众号，免费领学习资料

                                                                                    点“赞”和“在看”哦