人工智能数学基础--导数3：隐函数求导、对数求导法、参数方程求导法

一、隐函数概念

用y=f(x)这种方式定义的函数叫显函数，而隐函数是指没有使用这种方式定义，而是用类似F(x,y)=0这种方程方式来定义x和y关系的方式。

一般地，如果变量x和y满足一个方程F(x,y)=0，在一定条件下，当x取某区间内的任一值时，相应地总有满足这方程的唯一的y值存在，那么就说方程(x,y)=0在该区间内确定了一个隐函数。

把一隐函数化成显函数，叫做隐函数的显化。例如从方程x+y-1=0解出y=1-x，就把隐函数化成了显函数。隐函数的显化有时是有困难的，甚至是不可能的，但在实际问题中，有时需要计算隐函数的导数，因此我们希望有一种方法，不管隐函数能否显化，都能直接由方程算出它所确定的隐函数的导数来。

二、隐函数求导

隐函数实际上是一个方程，对于方程F(x,y)=0，可以对该方程两边对x求导，求导的结果还是一个方程。但求导中要注意，该方程隐含了y=f(x)，因此y不能看做常数处理。例如，针对方程：

xy=0

两边对x求导，可以得到的方程是：(xy）’=x’y+y’x=y+xy’=0

这样就能得到一个关于x、y、y’的方程，如果能将y’用x和y的方式表达出来，就得到了隐函数y的导数公式，当点(x0,y0)的坐标值确定时，在该点的导数值就能确定。

为了清楚说明，下面贴一个书中的例子：

三、对数求导法求导

求函数y=f(x)的导数在某些情况下，将函数两边先同时进行取对数运算再求导有助于化复杂为简单。老猿认为这是因为对数可以把指数或求根运算转换为乘积运算，可以把乘积运算转换为加减运算，实现了运算的降维。

指数运算转换为乘积运算的案例请见《y=x^sinx（y=x的sinx次方）为什么不能用复合函数直接求导数？》。

乘积、方根运算转换请见书中如下案例：

四、参数方程求导法

前面第二部分介绍的隐函数是对F(x,y)=0的方程求导，但有时x和y不是建立直接关系，而是各自与第三个参数建立方程关系，此时的方程就是参数方程。

一般地，方程组：

x=g(t)

y=h(t)

确定了y与x之间的函数关系，上述方程组就是参数方程，由该参数方程确定的y与x的关系函数y=f（x）就称为参数方程确定的函数。

针对参数方程确定的函数y=f(x)求导，由于二者之间都是通过t关联，要将其表达为y=f(x)方式需要去除参数t，但有些情况t不容易去掉，这时可能可以通过参数方程计算出y=f(x)的导数。

上述参数方程所确定的y关于x的函数的求导公式如下：

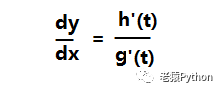
如果h(t)、g(t)是二阶可导的，那么从上述一阶导数可以得到函数对应的二阶导求导公式如下：

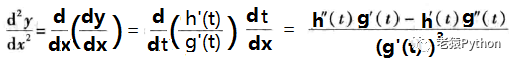
参数方程求导的一个应用案例

五、小结

本文介绍了利用隐函数、对数、以及参数方程求导的概念和方法。

说明：

本文内容是老猿学习同济版高数的总结，有需要原教材电子版的，请扫博客首页左边二维码加微信公号，根据加微信公号后的自动回复操作。

更多人工智能数学基础请参考专栏《人工智能数学基础》。