↑↑↑点击上方蓝字，回复资料，10个G的惊喜

仅作学术分享，不代表本公众号立场，侵权联系删除

转载于：作者：Criss，来源：机器学习与生成对抗网络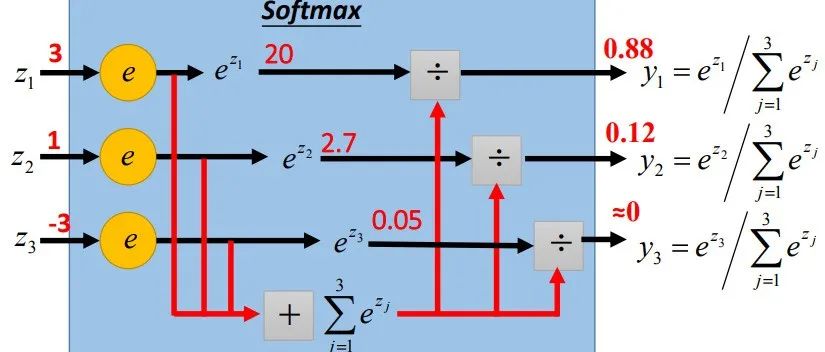

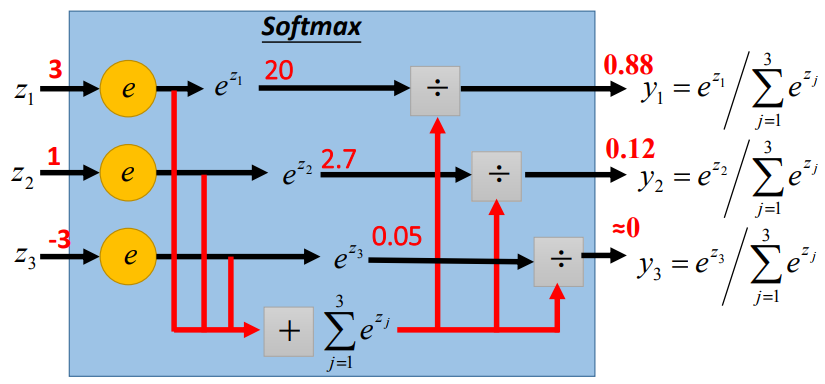
derivative of softmax

1.1 derivative of softmax

一般来说，分类模型的最后一层都是softmax层，假设我们有一个

3

分类问题，那对应的softmax层结构如下图所示（一般认为输出的结果

y_i

即为输入

x

属于第i类的概率）：

假设给定训练集

\{ (x_1, c_1), \dots, (x_m, c_m) \}

，分类模型的目标是最大化对数似然函数

L(\theta)

，即

通常来说，我们采取的优化方法都是gradient based的（e.g., SGD），也就是说，需要求解

\frac{\partial L(\theta)}{\partial \theta}

。而我们只要求得

\frac{\partial L(\theta)}{\partial z_i}

，之后根据链式法则，就可以求得

\frac{\partial L(\theta)}{\partial \theta}

，因此我们的核心在于求解

\frac{\partial L(\theta)}{\partial z_i}

，即

由上式可知，我们只需要知道各个样本

j

的

\frac{\partial}{\partial z_i} \ln P(c_j \vert x_j ; \theta)

，即可通过求和求得

\frac{\partial L(\theta)}{\partial z_i}

，进而通过链式法则求得

\frac{\partial L(\theta)}{\partial \theta}

。因此下面省略样本下标j，仅讨论某个样本

(x, c)

。

实际上对于如何表示

x

属于第几个类，有两种比较直观的方法：

一种是直接法（i.e., 用 $c=3$ 来表示x属于第3类），则 $P(c \vert x ; \theta)=\prod_n {y_n}^{\mathbb{1}(c=n)}$ ，其中 $\mathbb{1}(\bullet)$ 为指示函数；
另一种是one-hot法（i.e., 用 $c= [0 \quad 0 \quad 1]^T$ 来表示x属于第三类），则 $P(c \vert x ; \theta)=\prod_n {y_n}^{c_n}$ ，其中 $c_n$ 为向量 $c$ 的第 $n$ 个元素。
p.s., 也可以将one-hot法理解为直接法的实现形式，因为one-hot向量实际上就是 $\mathbb{1}(c=n)$ 。

为了方便，本文采用one-hot法。于是，我们有：

1.2 softmax & sigmoid

再补充一下softmax与sigmoid的联系。当分类问题是二分类的时候，我们一般使用sigmoid function作为输出层，表示输入

x

属于第1类的概率，即

P(1 \vert x ; \theta) = \frac{1}{1+e^{-z}}.

然后利用概率和为1来求解

x

属于第2类的概率，即

P(2 \vert x ; \theta) = 1 - P(1 \vert x ; \theta).

乍一看会觉得用sigmoid做二分类跟用softmax做二分类不一样：

在用softmax时，output的维数跟类的数量一致，而用sigmoid时，output的维数比类的数量少；
在用softmax时，各类的概率表达式跟sigmoid中的表达式不相同。

但实际上，用sigmoid做二分类跟用softmax做二分类是等价的。我们可以让sigmoid的output维数跟类的数量一致，并且在形式上逼近softmax。

通过上述变化，sigmoid跟softmax已经很相似了，只不过sigmoid的input的第二个元素恒等于0（i.e., intput为

[z \quad 0]^T

），而softmax的input为

[z_1 \quad z_2]^T

，下面就来说明这两者存在一个mapping的关系（i.e., 每一个

[z_1 \quad z_2]^T

都可以找到一个对应的

[z \quad 0]^T

来表示相同的softmax结果。不过值得注意的是，反过来并不成立，也就是说并不是每个

[z \quad 0]^T

仅仅对应一个

[z_1 \quad z_2]^T

）。

\begin{aligned} P(1 \vert x ; \theta) &= \frac{e^{z_1}}{e^{z_1}+e^{z_2}} \\ &= \frac{e^{z_1-z_2}}{e^{z_1-z_2}+e^{z_2-z_2}} \\ &= \frac{e^{z}}{e^{z}+e^{0}}. \\ \end{aligned}

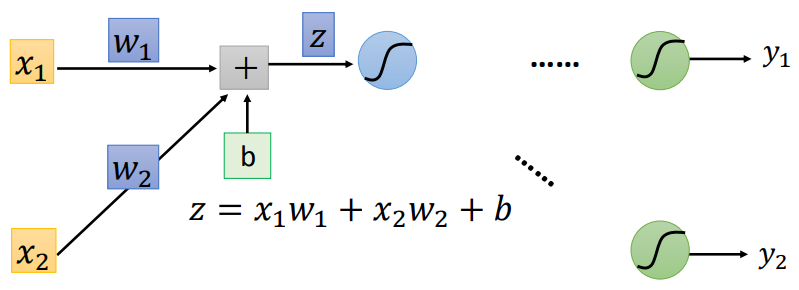
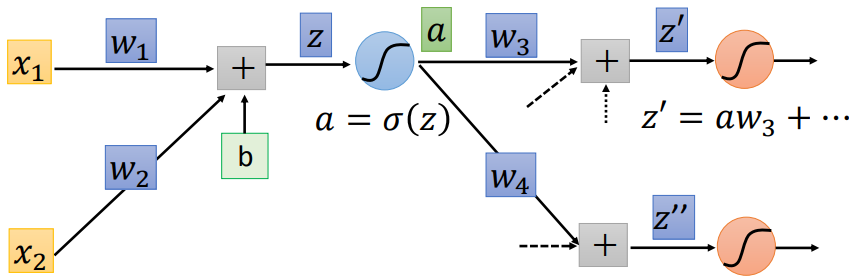
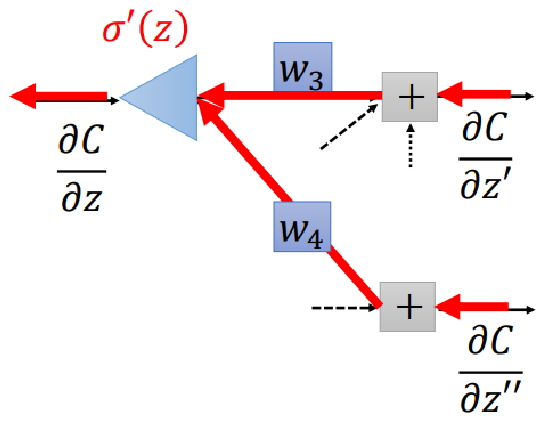
因此，用sigmoid做二分类跟用softmax做二分类是等价的。

02 backpropagation

一般来说，在train一个神经网络时（i.e., 更新网络的参数），我们都需要loss function对各参数的gradient，backpropagation就是求解gradient的一种方法。

假设我们有一个如上图所示的神经网络，我们想求损失函数

C

对

w_1

的gradient，那么根据链式法则，我们有

\frac{\partial C}{\partial w_1} = \frac{\partial C}{\partial z}\frac{\partial z}{\partial w_1}.

而我们可以很容易得到上述式子右边的第二项，因为

z = x_1 w_1 + x_2 w_2 +b

，所以有

\frac{\partial z}{\partial w_1} = x_1,

其中，

x_1

是上层的输出。

而对于式子右边的的第一项，可以进一步拆分得到

\frac{\partial C}{\partial z} = \frac{\partial C}{\partial a}\frac{\partial a}{\partial z}.

我们很容易得到上式右边第二项，因为

a=\sigma(z)

，而激活函数

\sigma

（e.g., sigmoid function）是我们自己定义的，所以有

\frac{\partial a}{\partial z} = \sigma^\prime(z)，

其中，

z

是本层的线性输出（未经激活函数）。

观察上图，我们根据链式法则可以得到

\frac{\partial C}{\partial a} = \frac{\partial C}{\partial z^\prime}\frac{\partial z^\prime}{\partial a} + \frac{\partial C}{\partial z^{\prime\prime}}\frac{\partial z^{\prime\prime}}{\partial a}.

其中，根据

z^\prime = aw_3 + \dots

可知

\begin{aligned} \frac{\partial z^\prime}{\partial a} &= w_3 \\ \frac{\partial z^{\prime\prime}}{\partial a} &= w_4. \end{aligned}

w_3

和

w_4

的值是已知的，因此，我们离目标

\frac{\partial C}{\partial a}

仅差

\frac{\partial C}{\partial z^\prime}

和

\frac{\partial C}{\partial z^{\prime\prime}}

了。接下来我们采用动态规划（或者说递归）的思路，假设下一层的

\frac{\partial C}{\partial z^\prime}

和

\frac{\partial C}{\partial z^{\prime\prime}}

是已知的，那么我们只需要最后一层的graident，就可以求得各层的gradient了。而通过softmax的例子，我们知道最后一层的gradient确实可求，因此只要从最后一层开始，逐层向前，即可求得各层gradient。

因此我们求

\frac{\partial C}{\partial z}

的过程实际上对应下图所示的神经网络（原神经网络的反向神经网络）：

综上，我们先通过神经网络的正向计算，得到

x_1

以及

z

，进而求得

\frac{\partial z}{\partial w_1}

和

\frac{\partial a}{\partial z}

；然后通过神经网络的反向计算，得到

\frac{\partial C}{\partial z^\prime}

和

\frac{\partial C}{\partial z^{\prime\prime}}

，进而求得

\frac{\partial C}{\partial a}

；然后根据链式法则求得

\frac{\partial C}{\partial w_1}

。这整个过程就叫做backpropagation，其中正向计算的过程叫做forward pass，反向计算的过程叫做backward pass。

03 derivative of CNN

卷积层实际上是特殊的全连接层，只不过：

神经元中的某些

w

为

0

；

神经元之间共享

w

。

具体来说，如下图所示，没有连线的表示对应的w为0：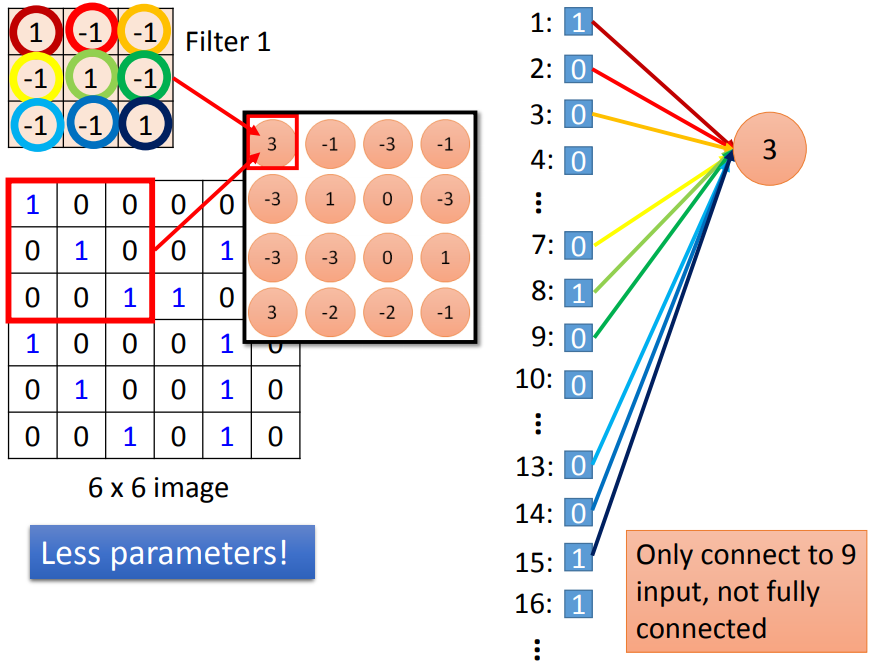

如下图所示，相同颜色的代表相同的

w

：

因此，我们可以把loss function理解为

C(z_1, z_2, \dots)

，然后求导的时候，根据链式法则，将相同w的gradient加起来就好了，即

\frac{\partial C}{\partial w} = \sum_i \frac{\partial C}{\partial z_i}\frac{\partial z_i}{\partial w}.

在求各个

\frac{\partial C}{\partial z_i}\frac{\partial z_i}{\partial w}

时，可以把他们看成是相互独立的

w

，那这样就跟普通的全连接层一样了，因此也就可以用backpropagation来求。

04 derivative of RNN

RNN按照时序展开之后如下图所示（红线表示了求gradient的路线）：

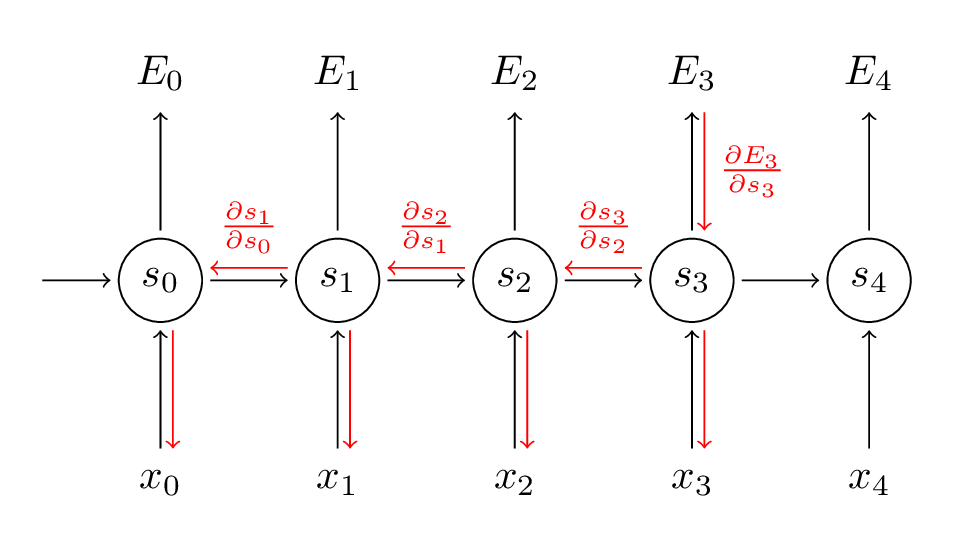
跟处理卷积层的思路一样，首先将loss function理解为

L(s_0, s_1, \dots)

，然后把各个w看成相互独立，最后根据链式法则求得对应的gradient，即

\frac{\partial L}{\partial w} = \sum_i\frac{\partial L}{\partial s_i}\frac{\partial s_i}{\partial w}.

由于这里是将RNN按照时序展开成为一个神经网络，所以这种求gradient的方法叫Backpropagation Through Time(BPTT)。

05 derivative of max pooling

一般来说，函数

max(x, y, \dots)

是不可导的，但假如我们已经知道哪个自变量会是最大值，那么该函数就是可导的（e.g., 假如知道y是最大的，那对y的偏导为1，对其他自变量的偏导为0）。

而在train一个神经网络的时候，我们会先进行forward pass，之后再进行backward pass，因此我们在对max pooling求导的时候，已经知道哪个自变量是最大的，于是也就能够给出对应的gradient了。

references：

http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML17_2.html

http://www.wildml.com/2015/10/recurrent-neural-networks-tutorial-part-3-backpropagation-through-time-and-vanishing-gradients/


也可以加一下老胡的微信
围观朋友圈~~~

推荐阅读

（点击标题可跳转阅读）

微软这个太强了

人工智能有多智障？

在公司内网搭建 pip 镜像站

【收藏】最全的Python常用标准库及第三方库

为什么美国学生学的数学比我们简单，却能做出很牛逼的东西？

求分享求点赞求在看！！

收藏 | 常见的神经网络求导总结！