作者注记

我是2017年11月开始接触深度学习，至今刚好五年。2019年10月入职上海交大，至今三年，刚好第一阶段考核。2022年8月19号，我在第一届中国机器学习与科学应用大会做大会报告，总结这五年的研究以及展望未来的方向。本文是该报告里关于理论方面的研究总结（做了一点扩展）。报告视频链接可以见：https://www.bilibili.com/video/BV1eB4y1z7tL/

我理解的深度学习

我原本是研究计算神经科学的，研究的内容，宏观来讲是从数学的角度理解大脑工作的原理，具体来说，我的研究是处理高维的神经元网络产生的脉冲数据，尝试去理解这些信号是如何处理输入的信号。但大脑过于复杂，维度也过于高，我们普通大脑有一千亿左右个神经元，每个神经元还和成千上万个其它神经元有信号传递，我对处理这类数据并没有太多信心，那阶段也刚好读到一篇文章，大意是把现阶段计算神经科学的研究方法用来研究计算机的芯片，结论是这些方法并不能帮助我们理解芯片的工作原理。另一个让我觉得非常难受的地方是我们不仅对大脑了解很少，还非常难以获得大脑的数据。于是，我们当时思考，能否寻找一个简单的网络模型，能够实现复杂的功能，同时我们对它的理解也很少的例子，我们通过研究它来启发我们对大脑的研究。

当时是2017年底，深度学习已经非常流行，特别是我的同学已经接触深度学习一段时间，所以我们迅速了解到深度学习。其结构和训练看起来足够简单，但能力不凡，而且与其相关的理论正处在萌芽阶段。因此，我进入深度学习的第一个想法是把它当作研究大脑的简单模型。 显然，在这种“类脑研究”的定位下，我们关心的是深度学习的基础研究。这里，我想区分深度学习的“理论”和“基础研究”。我认为“理论”给人一种全是公式和证明的感觉。而“基础研究”的范围听起来会更广阔一些，它不仅可以包括“理论”，还可以是一些重要的现象，直观的解释，定律，经验原则等等。这种区分只是一种感性的区分，实际上，我们在谈论它们的时候，并不真正做这么细致的区分。尽管是以深度学习为模型，来研究大脑为何会有如此复杂的学习能力，但大脑和深度学习还是有明显的差异。而我从知识储备、能力和时间上来看，都很难同时在这两个目前看起来距离仍然很大的领域同时深入。

于是我选择全面转向深度学习，研究的问题是，深度学习作为一个算法，它有什么样的特征。“没有免费的午餐”的定理告诉我们，当考虑所有可能的数据集的平均性能时，所有算法都是等价的，也就是没有哪一种算法是万能的。我们需要厘清深度学习这类算法适用于什么数据，以及不适用于什么数据。 事实上，深度学习理论并不是处于萌芽阶段，从上世纪中叶，它刚开始发展的时候，相关的理论就已经开始了，也有过一些重要的结果，但整体上来说，它仍然处于初级阶段。对我而言，这更是一个非常困难的问题。于是，我转而把深度学习当作一种“玩具”，通过调整各类超参数和不同的任务，观察它会产生哪些“自然现象”。设定的目标也不再高大上，而是有趣即可，发现有趣的现象，然后解释它，也许还可以用它来指导实际应用。在上面这些认识下，我们从深度神经网络训练中的一些有趣的现象开始。于我个人，我是从头开始学习写python和tensorflow，更具体是，从网上找了几份代码，边抄边理解。

神经网络真的很复杂吗？

在传统的学习理论中，模型的参数量是指示模型复杂程度很重要的一个指标。当模型的复杂度增加时，模型拟合训练数据的能力会增强，但也会带来在测试集上过拟合的问题。冯·诺依曼曾经说过一句著名的话，给我四个参数，我能拟合一头大象，五个参数可以让大象的鼻子动起来。

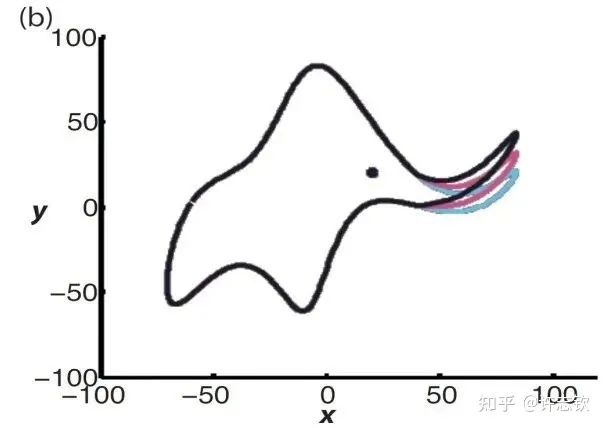
因此，传统建模相关的研究人员在使用神经网络时，经常会计算模型参数量，以及为了避免过拟合，刻意用参数少的网络。然而，今天神经网络能够大获成功，一个重要的原因正是使用了超大规模的网络。网络的参数数量往往远大于样本的数量，但却不像传统学习理论所预言的那样过拟合。这便是这些年受到极大关注的泛化迷团。实际上，在1995年，Leo Breiman在一篇文章中就已经指出了这个问题。在神经网络非常流行和重要的今天，这个迷团愈加重要。我们可以问：带有大量参数的神经网络真的很复杂吗？

答案是肯定的！上世纪八十年代末的理论工作证明当两层神经网络（激活函数非多项式函数）足够宽时，它可以以任意精度逼近任意连续函数，这也就是著名的“万有逼近”定理。实际上，我们应该问一个更加有意义的问题：在实际训练中，神经网络真的很复杂吗？ 逼近论证明的解在实际训练中几乎不可能遇到。实际的训练，需要设定初始值、优化算法、网络结构等超参数。对我们实际要有指导作用，我们就不能脱离这些因素来考虑泛化的问题，因为泛化本身就是依赖实际数据的问题。

两种简单偏好的现象

在学习与训练神经网络的过程中，我们很容易发现，神经网络的训练有一定的规律。在我们的研究中，有两种现象很有趣，在研究和解释它们的过程中，我们发现它们同样是很有意义的。我先简单介绍，然后再详细分别介绍。第一，我们发现神经网络在拟合数据的过程中经常会先学习低频，而后慢慢学习高频。我们把这个现象命名为频率原则（Frequency Principle, F-Principle）[1, 2]，也有其它工作把它称为Spectral bias。第二，我们发现在训练过程，有很多神经元的输入权重（向量）的方向会保持一致。我们称之为凝聚现象。这些输入权重一样的神经元对输入的处理是一样的，那它们就可以简化成一个神经元，也就是一个大网络可以简化成小网络[3, 4]。这两种现象都体现神经网络在训练过程中有一种隐式的简单偏好，低频偏好或者有效小网络偏好。低频偏好是非常普遍的，但小网络偏好是要在非线性的训练过程中才会出现的特征。

频率原则

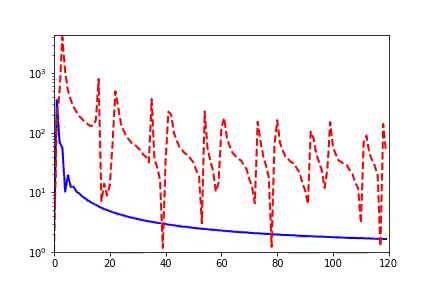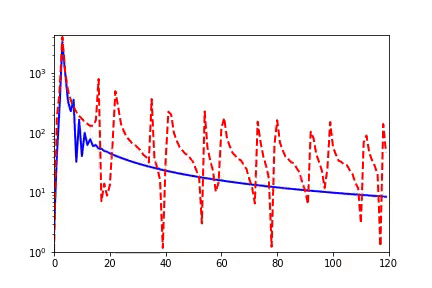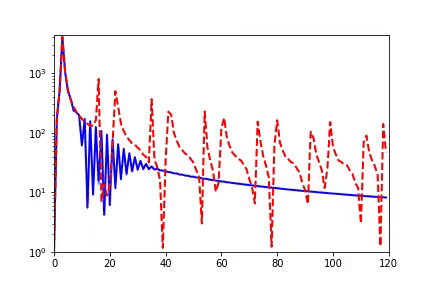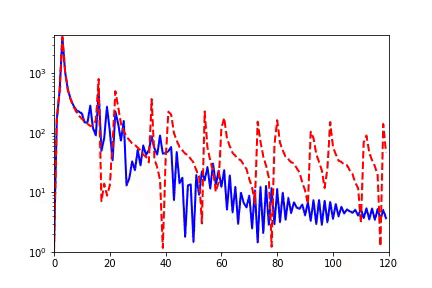
我早期在汇报频率原则相关的工作的时候，做计算数学的老师同学非常有兴趣，因为在传统的迭代格式中，例如Jacobi迭代，低频是收敛得非常慢的。多重网格方法非常有效地解决了这个问题。我们在实验中，也验证了神经网络和Jacobi迭代在解PDE时完全不一样的频率收敛顺序（如下图）[2, 5]。

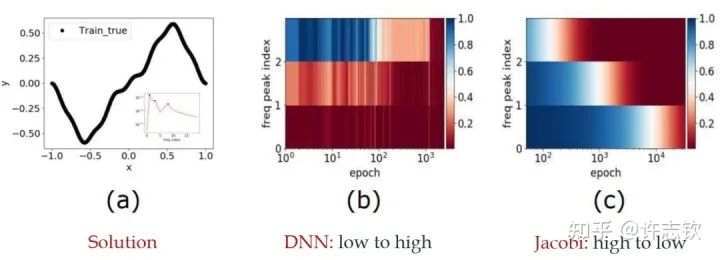
频率原则有多广泛呢？ 频率原则最开始是在一维函数的拟合中发现的。我在调参的过程中发现神经网络似乎总是先抓住目标函数的轮廓信息，然后再是细节。频率是一种非常适合用来刻画轮廓和细节的量。于是，我们在频率空间看神经网络的学习过程，发现非常明显地从低频到高频的顺序。

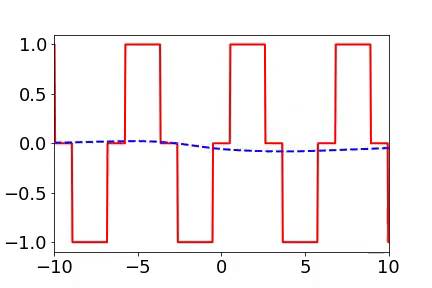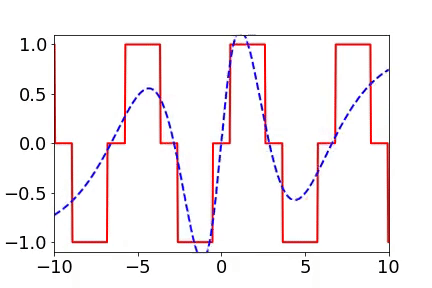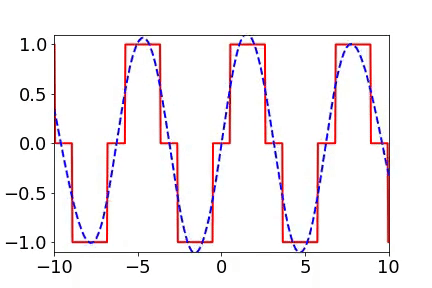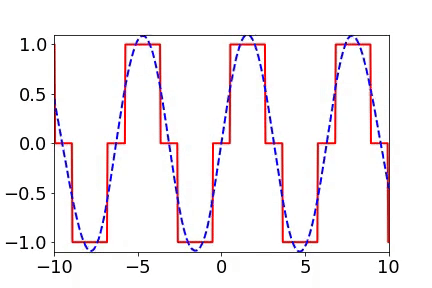
对于两维的函数，以图像为例，用神经网络学习从两维位置到灰度值的映射。神经网络在训练过程会慢慢记住更多细节。

对于更高维的例子，傅里叶变换是困难的，这也是不容易在高维的图像分类任务中发现频率原则的一个原因。我们的贡献还有一点就是用一个例子论证针对简单的低维问题的研究可以启发深度学习的基础研究。高维问题的频率需要多说两句。本质上，高频指的是输出对输入的变化非常敏感。比如在图片分类任务中，当一张图片被修改一点点，输出就发生变化。显然，这说的正是对抗样本。关于高维中验证频率原则，我们采用了降维和滤波的办法。一系列的实验都验证了频率原则是一个广泛存在的现象。

为什么会有频率原则呢？ 事实上，在自然界中大部分信号都有一个特征，强度随频率增加而衰减。一般我们见到的函数在频率空间也都有衰减的特征，特别是函数越光滑，衰减越快，连常见的ReLU函数在频率空间也是关于频率二次方衰减。在梯度下降的计算中，很容易得到低频信号对梯度的贡献要大于高频，所以梯度下降自然就以消除低频误差为主要目标[2]。对于一般的网络，我们有定性的理论证明[6]，而对于线性NTK区域的网络，我们有严格的线性频率原则模型揭示频率衰减的机制[7, 8, 9]。有了这个理解，我们也可以构造一些例子来加速高频的收敛，比如在损失函数中增加输出关于输入的导数项，因为求导在频率空间看，相当于在强度上乘以了一个其对应的频率，可以缓解高频的困难。这在求解PDE中很常见。

了解频率原则对我们理解神经网络有什么帮助吗？ 我们举两个例子。第一个是理解提前停止这个技巧。实际的训练中，一般都能发现泛化最好的点并不是训练误差最低的，通常需要在训练误差还没降得很低的时候，提前停止训练。实际数据大部分都是低频占优，而且基本都有噪音。噪音对低频的影响相对比较小，而对高频影响相对比较大，而神经网络在学习过程先学习低频，所以通过提前停止可以避免学习到过多被污染的高频而带来更好的泛化性能。另一个例子是，我们发现图像分类问题中，从图像到类别的映射通常也是低频占优，所以可以理解其良好的泛化。但对于定义在d维空间中的奇偶函数，其每一维的值只能取1或者-1。显然任何一维被扰动后，输出都会发生大的变化。这个函数可以被证明是高频占优的，而实际训练中，神经网络在这个问题中完全没有预测能力。我们还利用频率原则解释了为什么在实验中会观察到深度可以加快训练，核心的原因是越深的网络把目标函数变成一个越低频的函数，使学习变得容易 [10]。

除了理解，频率原则能对我们实际设计和使用神经网络产生什么指导吗？频率原则揭示了神经网络中存在高频灾难，这也引起了很多研究人员的注意，包括求解PDE、生成图像、拟合函数等。高频灾难带来的训练和泛化困难很难通过简单的调参来缓解。我们组提出了多尺度神经网络的方法来加速高频的收敛[11]。基本的想法是把目标函数在径向进行不同尺度的拉伸，尝试将不同频率的成分都拉伸成一致的低频，达到一致的快速收敛。实现也是非常之容易，仅需在第一隐藏层的神经元的输入乘以一些固定的系数即可。我们的一些工作发现调整激活函数对网络的性能影响很大[12]，用正弦余弦函数做第一个隐藏层的基可以有比较好的效果[13]。这个算法被华为的MindSpore所采用。径向拉伸的想法在很多其它的算法中也被采用，包括在图片渲染中非常出名的NerF（神经辐射场）。

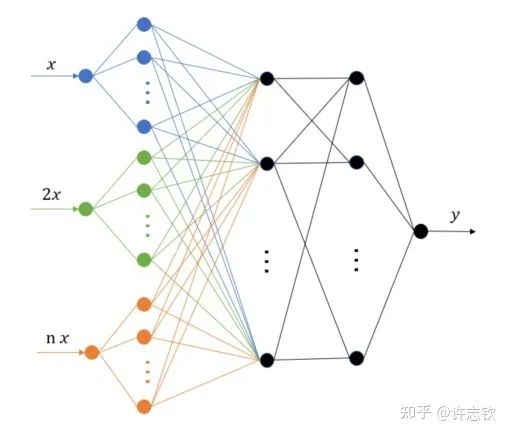
频率原则还有很多未解的问题需要被探索。 在非梯度下降训练的过程，比如粒子群算法怎么证明频率下降[14]？如何在理论上论证多尺度神经网络对高频的加速效果？是否有更稳定更快的高频加速算法？小波可以更细致的描述不同局部的频率特征，能否用小波更细节地理解神经网络的训练行为？数据量、网络深度、损失函数怎么影响频率原则？频率原则可以指导算法设计的理论，为训练规律提供一种“宏观”描述。对于“微观”机制，我们需要进一步研究。同样是低频到高频的学习过程，参数的演化可以非常不一样，比如一个函数可以用一个神经元表示，也可以用10个神经元（每个神经元的输出权重为原输出权重的1/10）一起表示，从输入输出函数的频率来看，这两种表示完全没有差别，那神经网络会选择哪一种表示，以及这些表示有什么差别？下面我们就要更细致地看参数演化中的现象。

参数凝聚现象

为了介绍参数凝聚现象我们有必要介绍一下两层神经元网络的表达

W是输入权重，它以内积的方式提取输入在权重所在的方向上的成分，可以理解为一种特征提取的方式，加上偏置项，然后再经过非线性函数（也称为激活函数），完成单个神经元的计算，然后再把所有神经元的输出加权求和。为了方便，我们记

对于ReLU激活函数，我们可以通过考虑输入权重的角度和神经元的幅度来理解每个神经元的特征：, 其中 。考虑用上面的两层神经网络来拟合四个一维的数据点。结合输入权重和偏置项，我们所关心的方向就是两维的方向，因此可以用角度来表示其方向。下图展示了，不同初始化下，神经网络的拟合结果（第一行），以及在训练前（青色）和训练后（红色）特征分布的图（第二行）

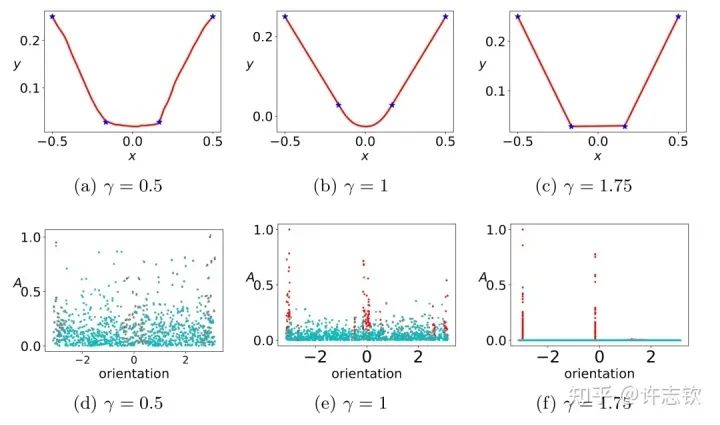
显然，随初始化尺度变小（从左到右，初始化尺度不断变小），神经网络的拟合结果差异很大，在特征分布上，当尺度很大（这里使用NTK的初始化），神经网络特征几乎不变，和random feature这类线性模型差不多，而随初始化变小，训练过程出现明显的特征变化的过程。最有意思的是，这些特征的方向聚集在两个主要的方向。我们把这种现象称为参数凝聚。 大量的实际问题告诉我们神经网络比线性的方法要好很多，那非线性过程所呈现的参数凝聚有什么好处吗？ 如下图展示的一个极端凝聚的例子，对于一个随机初始化的网络，经过短暂的训练后，每个隐藏层神经元的输入权重是完全一致的，因此这个网络可以等效成仅有一个隐藏层神经元的小网络。一般情况下，神经元会凝聚到多个方向。

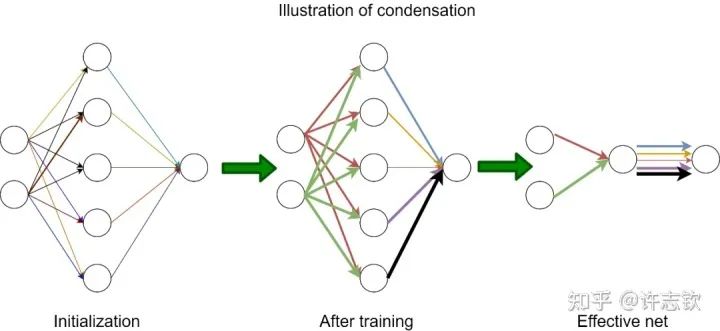
回顾在我们前面最开始提到的泛化迷团，以及我们最开始提出的问题“在实际训练中，神经网络真的很复杂吗？”，在参数凝聚的情况下，对于一个表面看起来很多参数的网络，我们自然要问：神经网络实际的有效参数有多少？ 比如我们前面看到的两层神经网络凝聚在两个方向的例子，实际上，这个网络的有效神经元只有两个。因此凝聚可以根据实际数据拟合的需求来有效地控制模型的复杂度。

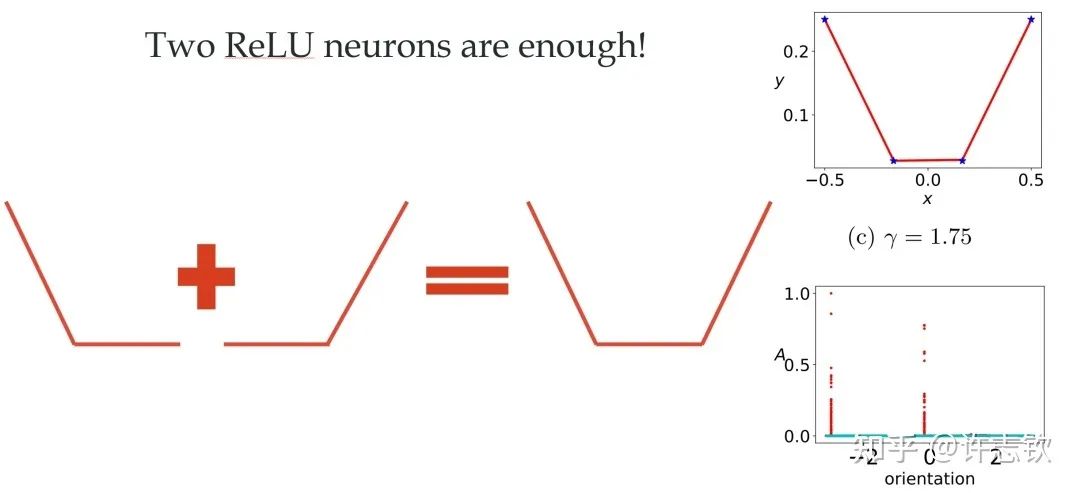
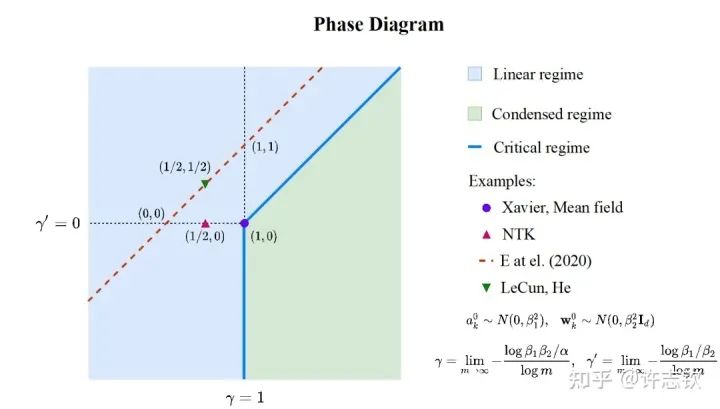
前面，我们只是通过一个简单的例子来呈现凝聚现象，接下来重要的问题是：参数凝聚是非线性过程中普遍的现象吗？ 在统计力学相图的启发下，我们在实验发现并理论推导出了两层无限宽ReLU神经网络的相图。基于不同的初始化尺度，以参数在训练前后的相对距离在无限宽极限下趋于零、常数、无穷作为判据，相图划分了线性、临界、凝聚三种动力学态（dynamical regime）。领域内的一系列理论研究（包括NTK，mean-field等）都可以在我们的相图中找到对应的位置[3]。

在三层无穷宽[15]的全连接网络中，我们实验证明在所有非线性的区域，参数凝聚都是一种普遍的现象。理论上，我们证明当初始化尺度足够小的时候，在训练初始阶段就会产生凝聚[4] 。有趣的是，我们在研究Dropout算法的隐式正则化的时候，发现Dropout算法会明显地促进参数凝聚地形成。 Dropout算法的想法是Hinton提出的，在神经网络的训练中，以一定概率p保留神经元，是一种常用的技巧，对泛化能力的提升有明显的帮助。我们首先来看一下拟合结果。下面左图是没有用Dropout的例子，放大拟合的函数，可以看到明显的小尺度的波动，右图是用了Dropout的结果，拟合的函数要光滑很多。

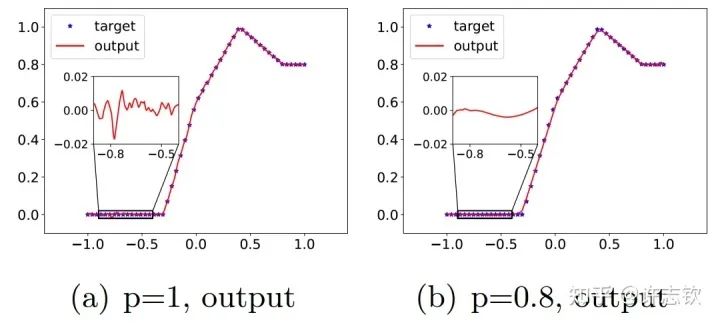
仔细看他们的特征分布时，可以看到训练前（蓝色）和训练后（橙色）的分布在有Dropout的情况下会明显不同，且呈现出明显地凝聚效应，有效参数变得更少，函数复杂度也相应变得简单光滑。

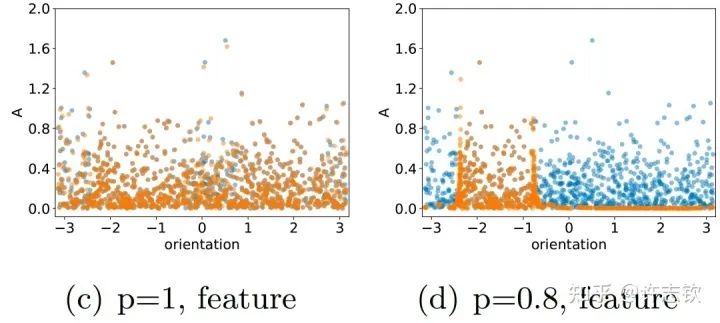
进一步，我们分析为什么Dropout会带来凝聚效应。我们发现Dropout的训练会带来一项特殊的隐式正则效应。我们通过下面的例子来理解这个效应。下面黄色和红色两种情况都能合成一个相同的向量，Dropout要求两个分向量的模长平方和要最小，那显然只有当两个向量的方向一致的时候，并且完全相等的时候，它们的模长平方和才能最小，对于w来说，这就是凝聚。

到目前，我们谈了参数凝聚使得神经网络的有效规模变得很小，那为什么我们不直接训练一个小规模的网络？大网络和小网络有什么差异？ 首先，我们用不同宽度的两层网络来拟合同一批数据，下图展示了它们的损失下降的过程。

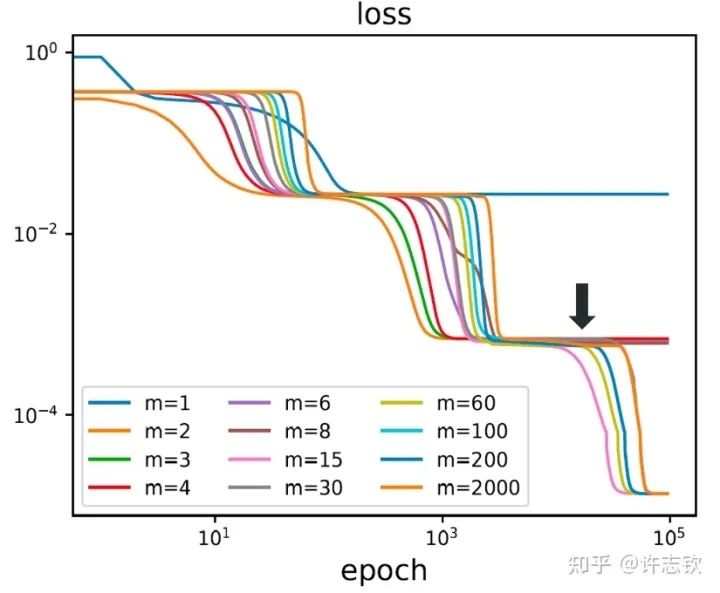
不同宽度的网络的损失函数表现出了高度的相似性，它们会在共同的位置发生停留。那在共同的台阶处有什么相似性呢？下面左图可以看到，对于上述箭头指示的台阶，不同宽度网络的输出函数非常靠近。更进一步看它们的特征图（下右图），它们都发生了强烈的凝聚现象。这些体现了它们的相似性。

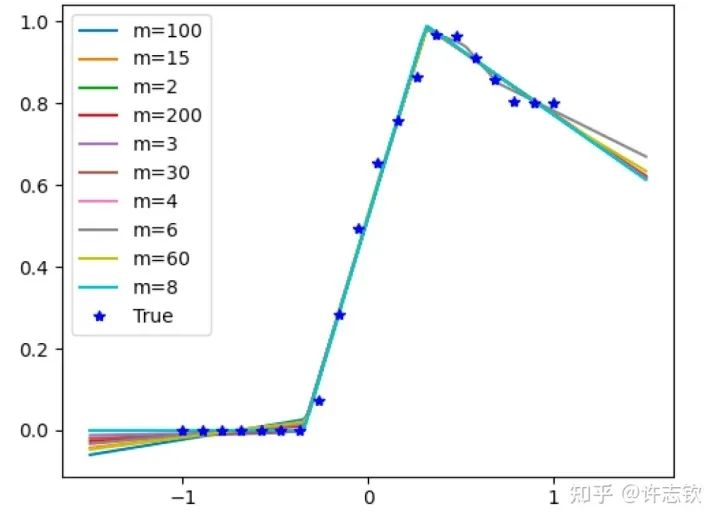
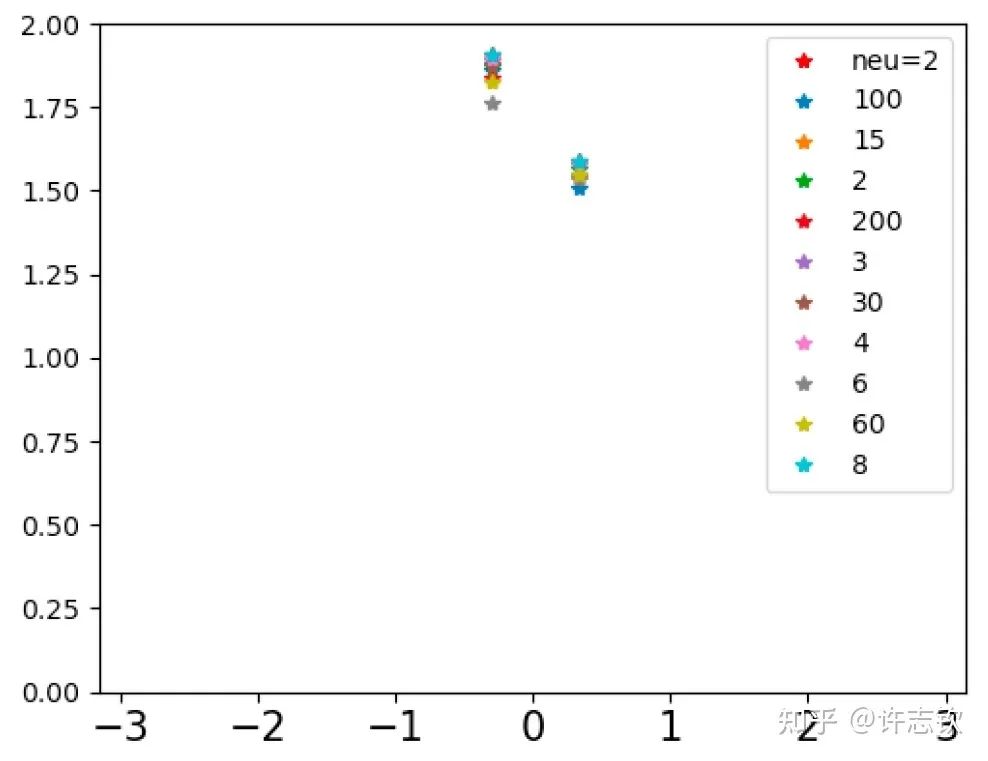
如果再仔细观察他们的损失图，可以发现当宽度增加的时候，网络的损失函数更容易下降，比如前面箭头指的地方，相对小的网络就停留在台阶上，大的网络的损失才继续下降。从实验上可以看出，大网络凝聚时虽然和小网络在表达能力类似，但看起来大网络更容易训练。怎么解释不同宽度的网络的相似性以及大网络的优势？ 在一个梯度下降的训练过程，出现平台的原因很可能是因为训练路径经历某个鞍点（附近有上升方向也有下降方向的极值点）附近。不同宽度的网络似乎会经历相同的鞍点。但参数量不同的网络，它们各自的鞍点生活在不同维度的空间，怎么会是同一点呢？

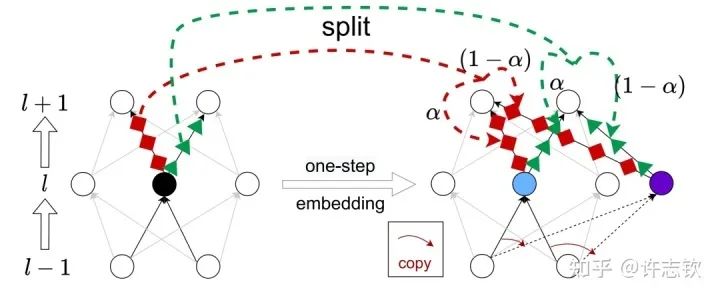
我们证明了不同宽度的网络的损失景观的极值点存在一个嵌入原则(Embedding Principle)[16], 即一个神经网络的损失景观中 “包含”所有更窄神经网络损失景观的所有临界点（包括鞍点、局部最优点和全局最优点等）。简单地说，就是一个网络处理临界点时，通过一些特定的嵌入方式，可以把这个网络嵌入到一个更宽的网络中，嵌入过程能够保持网络输出不变以及宽网络仍然处于临界点。最简单的嵌入方式正是凝聚的逆过程，比如下图是一种一步嵌入方式。更一般的嵌入方式我们在Journal of Machine Learning第一期的文章里[17]有详细讨论。

嵌入原则揭示了不同宽度网络的相似性，当然也提供了研究它们差异性的手段。由于在嵌入的过程中有自由参数，因此在更大网络的临界点的退化程度越大。同样的，一个大网络的损失景观里的临界点，如果它来源于更简单的网络的临界点的嵌入，那么它的退化程度也越大（直观可以理解它占的空间越大）。我们就可以猜测这些越简单的临界点越有可能被学习到。

另外，我们在理论上证明，在嵌入的过程中，临界点附近的下降方向、上升方向都不会变少。这告诉我们，一个鞍点被嵌入到一个更大的网络以后，它不可能变成一个极小值点，但一个极小值点被嵌入到大网络以后，它很有可能会变成鞍点，产生更多的下降方向。我们在实验上也证明了嵌入过程会产生更多下降方向。

因此，我们有理由相信，大网络尽管凝聚成有效的小网络，但它会比小网络更容易训练。也就是大网络既可以控制模型的复杂度（可能带来更好的泛化），又可以使训练更容易。 我们的工作还发现了在深度上神经网络损失景观的嵌入原则[18]。关于凝聚现象，同样还有很多问题值得继续深入。下面是一些例子。除了初始训练外，训练过程中的凝聚现象产生的机制是什么？不同的网络结构是否有凝聚现象？凝聚的过程和频率原则有什么联系？凝聚怎么定量地和泛化建立联系？

总结

过去五年，在深度学习的基础研究方面，我们主要围绕频率原则和参数凝聚两类现象展开工作。从发现它们，意识到他们很有趣，再到解释它们，并在一定程度上基于这些工作去理解深度学习的其它方面和设计更好的算法。未来五年，我们将在深度学习的基础研究和AI for Science方面深入钻研。

参考文献

[1] Zhi-Qin John Xu*, Yaoyu Zhang, and Yanyang Xiao, Training behavior of deep neural network in frequency domain, arXiv preprint: 1807.01251, (2018), ICONIP 2019.

[2] Zhi-Qin John Xu* , Yaoyu Zhang, Tao Luo, Yanyang Xiao, Zheng Ma, Frequency Principle: Fourier Analysis Sheds Light on Deep Neural Networks, arXiv preprint: 1901.06523, Communications in Computational Physics (CiCP).

[3]Tao Luo#,Zhi-Qin John Xu #, Zheng Ma, Yaoyu Zhang*, Phase diagram for two-layer ReLU neural networks at infinite-width limit, arxiv 2007.07497 (2020), Journal of Machine Learning Research (2021)

[4]Hanxu Zhou, Qixuan Zhou, Tao Luo, Yaoyu Zhang*, Zhi-Qin John Xu*, Towards Understanding the Condensation of Neural Networks at Initial Training. arxiv 2105.11686 (2021), NeurIPS2022.

[5] Jihong Wang,Zhi-Qin John Xu*, Jiwei Zhang*, Yaoyu Zhang, Implicit bias in understanding deep learning for solving PDEs beyond Ritz-Galerkin method, CSIAM Trans. Appl. Math.

[6] Tao Luo, Zheng Ma,Zhi-Qin John Xu, Yaoyu Zhang, Theory of the frequency principle for general deep neural networks, CSIAM Trans. Appl. Math., arXiv preprint, 1906.09235 (2019).

[7] Yaoyu Zhang, Tao Luo, Zheng Ma,Zhi-Qin John Xu*, Linear Frequency Principle Model to Understand the Absence of Overfitting in Neural Networks. Chinese Physics Letters, 2021.

[8] Tao Luo*, Zheng Ma,Zhi-Qin John Xu, Yaoyu Zhang, On the exact computation of linear frequency principle dynamics and its generalization, SIAM Journal on Mathematics of Data Science (SIMODS) to appear, arxiv 2010.08153 (2020).

[9]Tao Luo*, Zheng Ma, Zhiwei Wang, Zhi-Qin John Xu, Yaoyu Zhang, An Upper Limit of Decaying Rate with Respect to Frequency in Deep Neural Network, To appear in Mathematical and Scientific Machine Learning 2022 (MSML22),

[10] Zhi-Qin John Xu* , Hanxu Zhou, Deep frequency principle towards understanding why deeper learning is faster, AAAI 2021, arxiv 2007.14313 (2020)

[11] Ziqi Liu, Wei Cai,Zhi-Qin John Xu* , Multi-scale Deep Neural Network (MscaleDNN) for Solving Poisson-Boltzmann Equation in Complex Domains, arxiv 2007.11207 (2020) Communications in Computational Physics (CiCP).

[12] Xi-An Li,Zhi-Qin John Xu* , Lei Zhang, A multi-scale DNN algorithm for nonlinear elliptic equations with multiple scales, arxiv 2009.14597, (2020) Communications in Computational Physics (CiCP).

[13] Xi-An Li,Zhi-Qin John Xu, Lei Zhang*, Subspace Decomposition based DNN algorithm for elliptic type multi-scale PDEs. arxiv 2112.06660 (2021)

[14]Yuheng Ma,Zhi-Qin John Xu*, Jiwei Zhang*, Frequency Principle in Deep Learning Beyond Gradient-descent-based Training, arxiv 2101.00747 (2021).

[15]Hanxu Zhou, Qixuan Zhou, Zhenyuan Jin, Tao Luo, Yaoyu Zhang,Zhi-Qin John Xu*, Empirical Phase Diagram for Three-layer Neural Networks with Infinite Width. arxiv 2205.12101 (2022), NeurIPS2022.

[16]Yaoyu Zhang*, Zhongwang Zhang, Tao Luo,Zhi-Qin John Xu*, Embedding Principle of Loss Landscape of Deep Neural Networks. NeurIPS 2021 spotlight, arxiv 2105.14573 (2021)

[17] Zhongwang Zhang,Zhi-Qin John Xu*, Implicit regularization of dropout. arxiv 2207.05952 (2022)

往期精彩回顾




适合初学者入门人工智能的路线及资料下载
(图文+视频)机器学习入门系列下载
机器学习及深度学习笔记等资料打印
《统计学习方法》的代码复现专辑
机器学习交流qq群955171419，加入微信群请扫码