学习编译原理Time08 ~ 确定的有穷自动机及算法实现
小浩笔记
共 923字，需浏览 2分钟
·
2021-04-27 19:33
有穷自动机(FA)分为确定的有穷自动机(DFA)和不确定的有穷自动机(NFA).
本笔记主要记录的是确定的有穷自动机(DFA)
M=(S , ∑ , δ , s0, F )
S：有穷状态集
∑：输入字母表，即输入符号集合。假设 ε 不是∑中的元素
δ：将S X ∑映射到S的转换函数。 
s ∈S ，a∈∑，δ(s,a)表示从状态s出发，沿着标号为a的边所能到达的状态
s0：开始状态(或初始状态)，s0∈S
F：接收状态(或终止状态)集合，F
S
示例一个确定的有穷自动机如下：
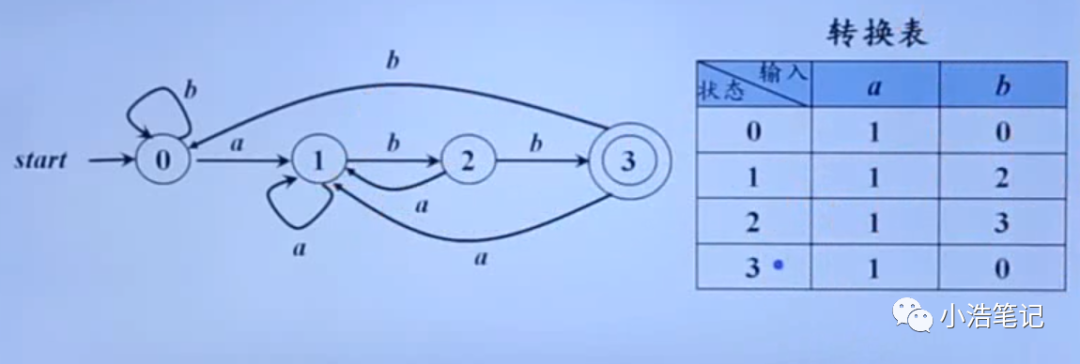
根据转换图可以看出，状态0遇到符号a的时候，就进入状态1，或状态0遇到符号b的时候，依然还是状态0，同样的道理，状态1遇到符号a的时候，还保持状态1，遇到符号b的时候就进入状态2；状态2遇到符号1的时候回到状态1，遇到符号b的时候进入状态3；状态3有个圆点表示终态，状态遇到符号a就进入状态1，遇到符号符号b就回到状态0。转换表也可以表示确定的有穷自动机。
接下来谈谈DFA的算法实现
输入：以文件结束符eof结尾的字符串x。DFA的开始状态s0，接收状态集F，转换函数move。
输出：如果DFA成功接收字符串x，则回答“yes”，否则回答“no”。
方法：将下述算法应用于输入串x。
s=s0;
c=nextChar();
while(c!=eof)
{
s=move(s,c);
c=nextChar();
}
if(s 在 F 中)
return "yes";
else
return "no";函数nextChar()返回输入串x的下一个符号
函数move(s, c)表示从状态s出发，沿着标记为c的边所能到达的状态
小浩笔记
评论