Im2Col+GEMM的改进方法MEC,一种更加高效的卷积计算策略
【GiantPandaCV导语】大家好,国庆闲在家里偶然看到了这篇对Im2Col+GEMM实现卷积进行改进的文章,然后去读了读顺便实现了一下,并在本文给出了一个测试结果。从结果来看,这个算法在速度和内存消耗都优于Im2Col+GEMM方式的卷积,想更多的知识和BenchMark可以阅读本文和原始论文。原论文地址:https://arxiv.org/abs/1706.06873v1 。本文复现代码开源在:https://github.com/BBuf/Memory-efficient-Convolution-for-Deep-Neural-Network
1. 前言
前面介绍了Im2Col+GEMM来实现卷积以在某些条件下获得更好的访存和计算效率,详见:详解Im2Col+Pack+Sgemm策略更好的优化卷积运算 。然后,最近偶然发现了Im2Col+GEMM的一个改进版本即MEC: Memory-efficient Convolution for Deep Neural Network ,这是发表在ICML 2017的文章,它主要优化了Im2Col+GEMM计算策略中的内存消耗,并且也能提升一点速度,是一个不错的卷积加速算法。所以我在这里结合论文然后复现了一下代码实现来为分享一下。
2. 背景介绍
当前的CNN模型一般只在最后一层使用全连接层,也即是说CNN的主体是由卷积层构成的。因此,对卷积层的加速对整个网络的性能非常关键。目前,对卷积层的计算一般有以下几种方式:
Im2Col+GEMM。Caffe/DarkNet/MxNet多种框架都使用了这种计算方法,因为将卷积操作转化为矩阵运算之后就可以方便的使用很多矩阵加速库如MKL,OpenBlas,Eigen等等。想详细了解这个算法的读者可以点一下上一节的链接。 WinoGrad算法。前面已经详细介绍过WinoGrad这种卷积加速算法,请点击:详解卷积中的Winograd加速算法 FFT加速。时域的卷积等于频域的乘积,我们可以把卷积运算转换为一个简单的乘法问题,这个并不是很多见,后面有时间我会考虑给大家分享一下如何用FFT完成卷积层计算加速的。
例如FaceBook研发的NNPACK加速包就是将FFT和WinoGrad进行结合,来对卷积运算进行加速。
从Im2Col+GEMM和WinoGrad的实现来看,虽然他们的执行效率都相比原始的卷积实现有所提升,但它们的内存占用都比较高,因为要存储中间结果比如Im2Col的转换结果(如Figure1所示),WinoGrad中的G,V,A矩阵等。

所以,MEC改进了Im2Col+GEMM的策略,目的是减少它的内存消耗同时提升一点速度。
3. MEC算法原理
在正式介绍这个算法之前先规定一些数学符号以及它代表的含义,如Table1所示:

3.1 MEC算法初级版
下面先介绍一下MEC算法的初级版本,我们以输入特征图大小为,输入卷积核大小为以及滑动步长为1的卷积层为例,这里先不考虑BatchSize和Channel维度,即我们只需要将输入特征图当成一个通道数为的普通的矩阵即可,如Figure2所示:
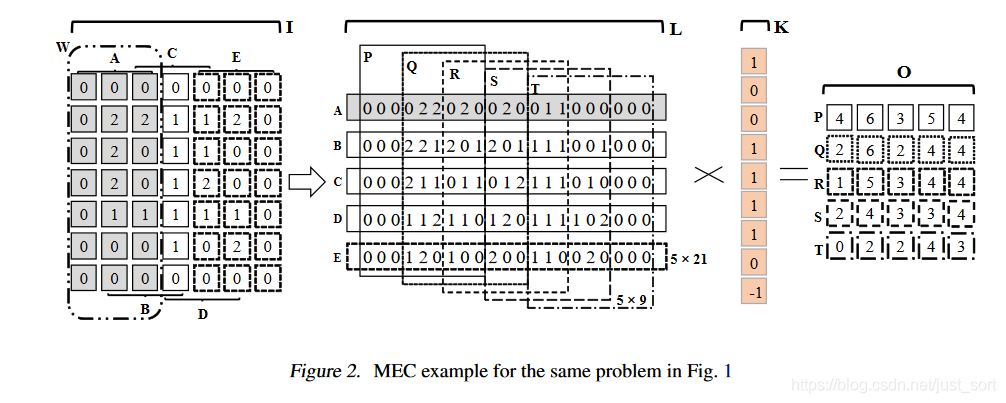
下面的Algorithm1展示了这个算法的流程:

我们要结合Figure2来看一下这个伪代码,这里的意思就是说:
因为是卷积,并且滑动步长为,所以这里循环取出A,B,C,D,E这5个子矩阵(在Figure2中看),每个子矩阵的维度都是,Figure2中代表特征图的高度即。 将A,B,C,D,E按照行优先展开并拼成一个大的中间矩阵,的维度是:。 从L中循环取出,,,,这个子矩阵,并计算次矩阵乘法,就获得了最终的输出特征图。
从上面的介绍中我们可以看到,MEC将Im2Col的过程分成了Height和Width两部分,于是需要存储的中间矩阵也大大减少了,因为如果是Im2Col,那么展开之后的矩阵大小是,但是现在MEC需要的矩阵大小只有,所以内存消耗降低了2倍。但是这样做可能带来的问题是,Im2Col+GEMM的一次矩阵乘法现在变成了多次小矩阵乘法,虽然这对并行计算是有利的,但如果使用OpenBlas库来计算则失去了它对大矩阵乘法计算的优势,所以从工程实现角度来说要达到论文给出的BenchMark那么高可能还需要一些奇淫技巧。
3.2 MEC算法高级版
将BatchSize和Channel维度加以考虑之后就获得了MEC算法的高级版,如Algorithm2所示:

然后下面的Figure3是它的示例图:
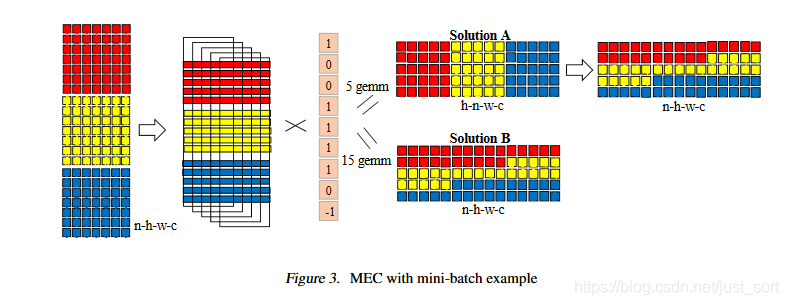
从伪代码里可以看到这里有2种计算方法:
Solution 1:Algorithm2中的第9-19行和Algorithm1中的方法完全一致,然后14-19行是对临时结果对做排列变化,即Figure3中的上半部分。 Solution 2:Algorithm2中的第21-25行。每次循环处理一个样本,不需要做额外的排列变化,即Figure3中的下半部分。
这两种计算方法的浮点乘法计算次数是完全一样的。但是,在实际操作中,子矩阵的数量对性能的影响是很大的,在Solution1中执行了次gemm,而Solution2中执行了次gemm,如果使用Blas矩阵计算库,那么这两种方法在特定硬件平台如GPU上哪一种更好是需要考虑的。因此,在Algorithm2的第8行使用了一个参数T来控制是使用Solution1还是Solution2,其中T是一个和硬件平台有关的参数。论文指出,如果是在GPU上,那么T取是一个不错的值。
4. 实验对比
论文使用C++在CPU/GPU上分别进行了实现以及性能测试,矩阵计算库使用了多线程OpenBlas,OpenMP,cuBLAS,数据类型为float32。下面的Table2展示了BenchMark使用的网络结构:
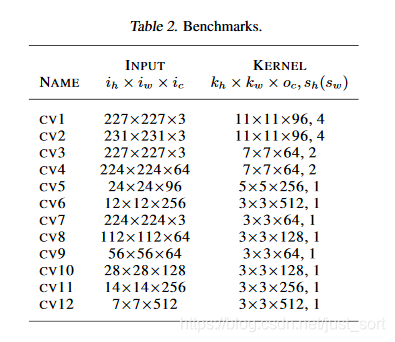
然后,下面是一些卷积加速算法和硬件平台绑定后的简称:

最后,我们直接抬出实验结果
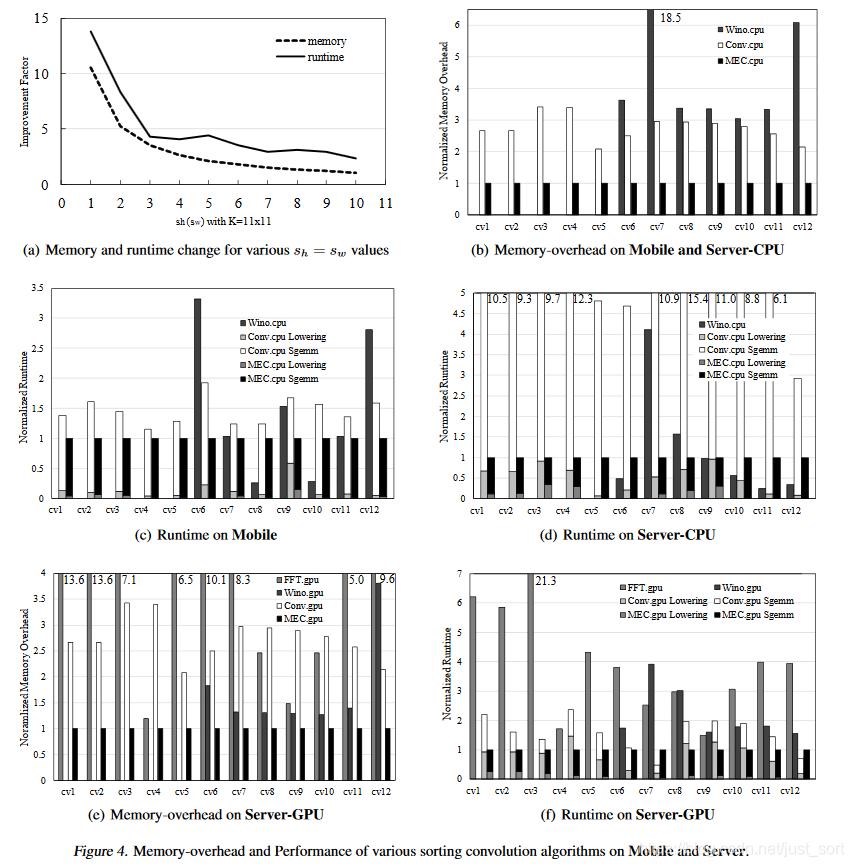
从实验结果可以看到,无论是从内存占用还是运算时间都相比于WinoGrad,Im2Col+GEMM,FFT有一些优势,不过这里并没有给出更多的实验对比结果例如和NNPACK以及CUDNN的对比。
5. 复现尝试(暂时只针对X86 CPU)
从理论介绍来看,这个算法实现起来也相对比较简单,接下来我就尝试实现一下这个算法。这个算法最核心的部分就是Im2Col以及MEC这种改进后的Im2Col方式,然后这个地方我是在x86平台上进行了复现和测试,所以选用了OpenBlas加速库来完成Im2Col后的矩阵运算。这个地方实现的是单通道的输入特征图(可以看成一张灰度图),分辨率是,然后卷积核是,然后通道数是64,这里直接随意给输入特征图和卷积核赋了值,因为这里只需要对比一下这两种实现的速度以及内存消耗。
我们首先来看Im2Col的实现:
// 原始的Im2Col
void im2col_cpu(float** src, const int &inHeight, const int &intWidth, const int &kHeight,
const int &kWidth, float* srcIm2col){
const int outHeight = inHeight - kHeight + 1;
const int outWidth = intWidth - kWidth + 1;
int cnt = 0;
for(int i = 0; i < kHeight; i++){
for(int j = 0; j < kWidth; j++){
int id = i * kWidth + j;
int ii = i;
for(int x = 0; x < outHeight; x++){
int jj = j;
for(int y = 0; y < outWidth; y++){
srcIm2col[cnt] = src[ii][jj];
jj += 1;
cnt++;
}
ii += 1;
}
}
}
}
结合一下文章开头部分的Im2Col的图可以更好的理解,这个地方就是将输入特征图通过Im2Col的方式放到一个数组里面,为什么是个数组而不是二维矩阵呢?这里只是将这个二维矩阵存成了一个数组,来方便后面调用cblas_sgemm接口,关于OpenBlas的介绍以及计算方式,函数接口可以查看参考中的资料2,这里就不过多介绍了。
然后对卷积核同样手动Im2Col即可:
// 构造输入矩阵
float **src = new float*[inHeight];
for(int i = 0; i < inHeight; i++){
src[i] = new float[inWidth];
for(int j = 0; j < inWidth; j++){
src[i][j] = 0.1;
}
}
// 构造kernel矩阵
float **kernel[kernel_num];
for(int i = 0; i < kernel_num; i++){
kernel[i] = new float*[kernel_h];
for(int j = 0; j < kernel_h; j++){
kernel[i][j] = new float[kernel_w];
for(int k = 0; k < kernel_w; k++){
kernel[i][j][k] = 0.2;
}
}
}
// 开始计时
struct timeval tstart, tend;
gettimeofday(&tstart, NULL);
// 对kernel进行Im2col
float* kernel2col = new float[kernel_num*kernel_h*kernel_w];
int cnt = 0;
for(int i = 0; i < kernel_num; i++){
for(int j = 0; j < kernel_h; j++){
for(int k = 0; k < kernel_w; k++){
kernel2col[cnt++] = kernel[i][j][k];
}
}
}
// 对输入矩阵Im2col
int outHeight = inHeight - kernel_h + 1;
int outWidth = inWidth - kernel_w + 1;
float *srcIm2col = new float[kernel_w * kernel_h * outWidth * outHeight];
im2col_cpu(src, inHeight, inWidth, kernel_h, kernel_w, srcIm2col);
接下来调用cblas_sgemm函数接口即可完成卷积层的计算,这个地方加入了计时函数,统计Im2Col+gemm的运行时间:
// 使用Blas库实现矩阵乘法
float *output = new float[kernel_num * outHeight * outWidth];
cblas_sgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,kernel_num,
outHeight*outWidth, kernel_w*kernel_h, 1,
kernel2col, kernel_h*kernel_w,
srcIm2col,outHeight * outWidth, 0, output, outHeight * outWidth);
// 结束计时
gettimeofday(&tend, NULL);
cout<<"im2colOrigin Total time cost: "<<(tend.tv_sec-tstart.tv_sec)*1000 + (tend.tv_usec-tstart.tv_usec)/1000<<" ms"<<endl;
在复现MEC的时候主要是对Im2Col的修改,代码实现如下,可以结合原理介绍中的图示进行查看,就很好理解了。
// MEC
void im2col_mec(float** src, const int &inHeight, const int &intWidth, const int &kHeight,
const int &kWidth, float* srcIm2col){
const int outHeight = inHeight - kHeight + 1;
const int outWidth = intWidth - kWidth + 1;
#pragma omp parallel for num_threads(THREAD_NUM)
for(int i = 0; i < outWidth; i++){
int outrow = 0;
for(int j = 0; j < inHeight; j++){
for(int k = i; k < i + kWidth; k++){
srcIm2col[outrow * outWidth + i] = src[j][k];
outrow++;
}
}
}
}
然后对Kernel的Im2col过程完全一致,只是在求输出矩阵的时候要用for循环去遍历一下每个子矩阵(这个地方是5个,参考一下原理部分的图),代码如下:
// 构造输入矩阵
float **src = new float*[inHeight];
for(int i = 0; i < inHeight; i++){
src[i] = new float[inWidth];
for(int j = 0; j < inWidth; j++){
src[i][j] = 0.1;
}
}
// 构造kernel矩阵
float **kernel[kernel_num];
for(int i = 0; i < kernel_num; i++){
kernel[i] = new float*[kernel_h];
for(int j = 0; j < kernel_h; j++){
kernel[i][j] = new float[kernel_w];
for(int k = 0; k < kernel_w; k++){
kernel[i][j][k] = 0.2;
}
}
}
// 开始计时
struct timeval tstart, tend;
gettimeofday(&tstart, NULL);
// 对kernel进行Im2col
float* kernel2col = new float[kernel_num*kernel_h*kernel_w];
int cnt = 0;
for(int i = 0; i < kernel_num; i++){
for(int j = 0; j < kernel_h; j++){
for(int k = 0; k < kernel_w; k++){
kernel2col[cnt++] = kernel[i][j][k];
}
}
}
// 对输入矩阵Im2col
int outHeight = inHeight - kernel_h + 1;
int outWidth = inWidth - kernel_w + 1;
float *srcIm2col = new float[outWidth * inHeight * kernel_w];
im2col_mec(src, inHeight, inWidth, kernel_h, kernel_w, srcIm2col);
// 使用Blas库实现矩阵乘法
float **output = new float*[outHeight];
#pragma omp parallel for num_threads(THREAD_NUM)
for(int i = 0; i < outHeight; i++){
output[i] = new float [kernel_num * outWidth];
cblas_sgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,kernel_num,
outWidth, kernel_w * kernel_h,1,
kernel2col, kernel_h * kernel_w,
srcIm2col + i * outWidth, outWidth, 0, output[i], outWidth);
}
// 结束计时
gettimeofday(&tend, NULL);
cout<<"MEC Total time cost: "<<(tend.tv_sec-tstart.tv_sec)*1000 + (tend.tv_usec-tstart.tv_usec)/1000<<" ms"<<endl;
这里实现的是MEC算法的初级版本,没有考虑Channel维度,对这个算法感兴趣的同学可以自行复现新增Channel维度的高级版算法。
本文的完整代码以及如何在X86编译运行请查看github:https://github.com/BBuf/Memory-efficient-Convolution-for-Deep-Neural-Network
6. 效果
测试了一下复现的MEC和原始的Im2Col+GEMM的速度和内存消耗,结果如下:
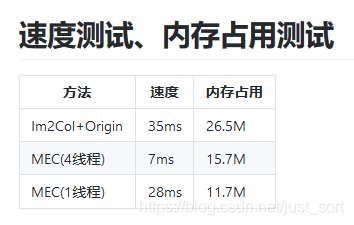
可以看到,在单线程的条件下,MEC的内存消耗明显比原始的Im2Col+GEMM更好并且速度也有一些提升。另外如果启用多线程那么速度也会有大幅度提升,注意在原始实现的版本中因为只有一个GEMM,所以整个算法无法并行。而在MEC的版本中拆成了5次GEMM,这对并行计算更加友好,因此获得了可观的加速,并且内存占用仍然优于原始版本。
7. 参考
资料1:https://blog.csdn.net/shuzfan/article/details/77427979 资料2:https://blog.csdn.net/yutianzuijin/article/details/90411622 https://github.com/CSshengxy/MEC
欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享,坚持原创,每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧
有对文章相关的问题,或者想要加入交流群,欢迎添加BBuf微信:
为了方便读者获取资料以及我们公众号的作者发布一些Github工程的更新,我们成立了一个QQ群,二维码如下,感兴趣可以加入。
