一、决策树概述

决策树算法易于理解、可解释性强，是一个非常常见并且优秀的机器学习算法，可分类，也可回归。现在许多最优秀的集成模型，基础也是决策树。因此，决策树系列算法是机器学习绕不过的大山。需要进行非常系统化、深刻化的学习和理解。

在信息论中一个属性的信息增益越大，表明该属性对样本的熵减少能力越强，也就是说确定这个属性会使系统越稳定有序（熵越小系统越稳定），那么该分区的纯度也就越高。

不论一个数据集有多少特征，每次划分数据集时只能选一个特征，那么第一次选择哪个特征作为划分的参考属性才能将数据更快的分类呢?

答案一定是分类能力最好的那个特征，但问题来了，如何判断哪一个特征分类能力最好呢？可以引入一个比较感性的概念，就是纯度，分裂后越纯越好，衡量纯度有三种常见的方法，不同的衡量方法可能会导致不同的分裂。

1） ID3 算法：Iterative Dichotomiser3，迭代二叉树三代,是最早提出的决策树算法，用信息增益作为分裂准则。

2） C4.5 算法：C4.5由J.Ross Quinlan在ID3的基础上提出的，他是 ID3 的改进版，用信息增益率作为分类准则。

3） CART算法：Classification and Regression Tree,分类回归树,用基尼指数作为分裂准则，这种算法即可以用于分类，也可以用于回归问题。

今天我们要讲的就是第一个算法：ID3 算法，其余两种算法将会后续推出详细的讲解，在下面的文章中，我会带着大家一步步的计算信息增益，让大家彻底理解ID3算法的原理。如果有不懂的，也可以加我交流：wuzhx2014

二、数据集介绍

下面是本例采用的数据集，包含了过去 14 天的天气因素 Outlook(天气)，Temp.(温度)，Humidity(湿度)、Wind(风力) 4 个特征、14 个样本，来学习一个是否去室外打球的决策树。

Day	Outlook	Temp.	Humidity	Wind	Decision
1	Sunny	Hot	High	Weak	No
2	Sunny	Hot	High	Strong	No
3	Overcast	Hot	High	Weak	Yes
4	Rain	Mild	High	Weak	Yes
5	Rain	Cool	Normal	Weak	Yes
6	Rain	Cool	Normal	Strong	No
7	Overcast	Cool	Normal	Strong	Yes
8	Sunny	Mild	High	Weak	No
9	Sunny	Cool	Normal	Weak	Yes
10	Rain	Mild	Normal	Weak	Yes
11	Sunny	Mild	Normal	Strong	Yes
12	Overcast	Mild	High	Strong	Yes
13	Overcast	Hot	Normal	Weak	Yes
14	Rain	Mild	High	Strong	No

对于决策树ID3算法，只有两个核心公式，计算经验熵和条件熵，我们简单回顾下：

经验熵：Entropy(S) = -∑ p(i) * log2p(i)

条件熵：Entropy(S|A) = ∑ [ p(S|A) * Entropy(S|A) ]

信息增益：Gain(S, A) = Entropy(S) -∑ [ p(S|A)* Entropy(S|A) ]

这些公式看起来可能会让人迷惑，我们从实际计算中，一步步来理解这些公式，理解了上面的三个公式，基本上也就理解了决策树这个算法。

三、经验熵计算

首先，我们需要计算整个数据集的经验熵，也就是固有的熵，数据集包含14个样本和两个类别：Yes and No，9个样本是Yes,5个样本是No。

标签	Yes	No	汇总
样本数	9	5	14
概率值	9/14	5/14	14/14

根据上述公式和统计数据，我们可以计算出数据集的经验熵

from math import log2Entropy(S) = -p(Yes)*log2p(Yes)-p(No)*log2p(No)= -(9/14)*log2(9/14)-(5/14)*log2(5/14)= 0.9402859586706311

经验熵计算完了，现在，我们要计算每个特征的条件熵，以及对应的信息增益，并对信息增益进行排序，选择增益最大的特征作为第一个分裂点进行分裂。

四、条件熵计算

完成了数据集经验熵的计算，就该计算每个特征分别的条件熵，以及对应的信息增益。

第一层分裂决策

数据集有四个特征，需要分别计算每个特征的条件熵，Outlook(天气)，Temp.(温度)，Humidity(湿度)、Wind(风力) 。

1、Wind条件熵

wind这个特征包含两个属性，weak and strong

Gain(Decision, Wind) = Entropy(Decision)- ∑ [ p(Decision|Wind)* Entropy(Decision|Wind)] = Entropy(Decision)-[p(Decision|Wind=Weak)*Entropy(Decision|Wind=Weak)] -[p(Decision|Wind=Strong)*Entropy(Decision|Wind=Strong)]

我们需要分别计算 (Decision|Wind=Weak) 和 (Decision|Wind=Strong)

Wind	Yes	No	样本数
Weak	6	2	8
Strong	3	3	6

1）Weak 属性熵计算

Day	Outlook	Temp.	Humidity	Wind	Decision
1	Sunny	Hot	High	Weak	No
3	Overcast	Hot	High	Weak	Yes
4	Rain	Mild	High	Weak	Yes
5	Rain	Cool	Normal	Weak	Yes
8	Sunny	Mild	High	Weak	No
9	Sunny	Cool	Normal	Weak	Yes
10	Rain	Mild	Normal	Weak	Yes
13	Overcast	Hot	Normal	Weak	Yes

Wind=Weak这个属性的子集，共有8个样本，其中2个No和8个Yes，计算该子集的熵如下：

Entropy(Decision|Wind=Weak) = –p(No)* log2p(No)–p(Yes) * log2p(Yes)= -(6/8)*log2(6/8)-(2/8)*log2(2/8)= 0.8112781244591328

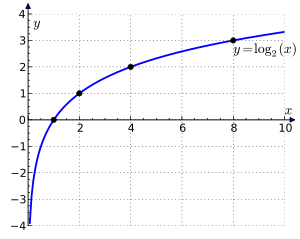
注意：如果类的实例数为0，而实例总数为n，则需要计算-(0/n) .log2(0/n)，定义0log20=0，熵只依赖于X的分布，与X的取值无关。这里，log(0）将等于-∞, 我们不能计算0次∞. 这是决策树应用程序中经常出现的一种特殊情况。即使编译器不能计算这个运算，我们也可以用微积分来计算，如果你想知道如何计算这个方程，请阅读这篇文章。

https://sefiks.com/2018/08/25/indeterminate-forms-and-lhospitals-rule-in-decision-trees/

2）Strong 属性熵计算

Day	Outlook	Temp.	Humidity	Wind	Decision
2	Sunny	Hot	High	Strong	No
6	Rain	Cool	Normal	Strong	No
7	Overcast	Cool	Normal	Strong	Yes
11	Sunny	Mild	Normal	Strong	Yes
12	Overcast	Mild	High	Strong	Yes
14	Rain	Mild	High	Strong	No

Wind = Strong 这个子集，一共有6个样本，其中3个Yes，3个No，计算其熵如下

Entropy(Decision|Wind=Strong) = –p(No)*log2p(No)-p(Yes)*log2p(Yes)= -(3/6)*log2(3/6)-(3/6)*log2(3/6)= 1.0

3）汇总计算

Wind	Yes	No	样本数
Weak	6	2	8
Strong	3	3	6

根据上面的统计数据，现在我们可以计算Wind特征的信息增益了

Gain(Decision,Wind)= Entropy(Decision)-[p(Decision|Wind=Weak)*Entropy(Decision|Wind=Weak)]-[p(Decision|Wind=Strong).Entropy(Decision|Wind=Strong)] = 0.940–[(8/14).0.811 ]–[(6/14). 1]= 0.940-(8/14)*0.811-(6/14)* 1 = 0.04799999999999999

Wind(风力)这个特征的信息增益计算结束了，现在，我们需要对其他特征应用相同的计算方法，计算出剩余每个特征的风险增益。

2、Outlook 条件熵

Outlook 这个特征有Sunny、Overcast、Rain这三个属性，分别计算每个属性的熵，然后再进行加权得到条件熵。

Outlook	Yes	No	样本数
Sunny	2	3	5
Overcast	4	0	4
Rain	3	2	5

1）Overcast

Day	Outlook	Temp.	Humidity	Wind	Decision
3	Overcast	Hot	High	Weak	Yes
7	Overcast	Cool	Normal	Strong	Yes
12	Overcast	Mild	High	Strong	Yes
13	Overcast	Hot	Normal	Weak	Yes

这个属性全部只有一个标签Yes，可以按下面的计算，但是会报错，可以直接按上面的规则计算(0/4)*log2(0/4)=0，所以可以知道Entropy(Decision|Outlook=Overcast)=0

Entropy(Decision|Outlook=Overcast)=–p(No)*log2p(No)–p(Yes)*log2p(Yes)=-(0/4)*log2(0/4)-(4/4)*log2(4/4) ValueError: math domain error

2）Rain

Day	Outlook	Temp.	Humidity	Wind	Decision
4	Rain	Mild	High	Weak	Yes
5	Rain	Cool	Normal	Weak	Yes
6	Rain	Cool	Normal	Strong	No
10	Rain	Mild	Normal	Weak	Yes
14	Rain	Mild	High	Strong	No

Rain这个属性有5个样本，其中2个No,3个Yes，按下面的方法计算该子集的熵

Entropy(Decision|Outlook=Rain) = -p(No)*log2p(No)-p(Yes)*log2p(Yes)= -(2/5)*log2(2/5)-(3/5)*log2(3/5)= 0.9709505944546686

3）Sunny

Day	Outlook	Temp.	Humidity	Wind	Decision
1	Sunny	Hot	High	Weak	No
2	Sunny	Hot	High	Strong	No
8	Sunny	Mild	High	Weak	No
9	Sunny	Cool	Normal	Weak	Yes
11	Sunny	Mild	Normal	Strong	Yes

Sunny这个属性也有有5个样本，其中2个No,3个Yes，按下面的方法计算该子集的熵

Entropy(Decision|Outlook=Sunny) = -p(No) * log2p(No) - p(Yes) *log2p(Yes)= -(2/5) * log2(2/5) - (3/5) *log2(3/5)= 0.9709505944546686

现在我们可以计算Outlook特征的信息增益了

Gain(Decision, Outlook) = Entropy(Decision)  –[p(Decision|Outlook=Overcast)*Entropy(Decision|Outlook=Overcast)]  –[p(Decision|Outlook=Rain)*Entropy(Decision|Outlook=Rain)   –[p(Decision|Outlook=Sunny)*Entropy(Decision|Outlook=Sunny)] = 0.940-(5/14)*0-(5/14)*0.9709-(5/14)*0.9709 = 0.24649999999999994

通过上面的计算，得到Outlook这个特征的信息增益为：Gain(Decision, Outlook)= 0.246，是不是非常简单呢。

3、Temp 特征的条件熵

Temp	Yes	No	样本数
Cool	3	1	4
Hot	2	2	4
Mild	4	2	6

1）Cool

Day	Outlook	Temp.	Humidity	Wind	Decision
5	Rain	Cool	Normal	Weak	Yes
7	Overcast	Cool	Normal	Strong	Yes
9	Sunny	Cool	Normal	Weak	Yes
6	Rain	Cool	Normal	Strong	No

Temp=Cool这个属性，一共有4个样本，3个Yes,1个No，计算熵如下：

Entropy(Decision|Temp=Cool) = -p(No)*log2p(No)-p(Yes)*log2p(Yes)= -(3/4)*log2(3/4)-(1/4)*log2(1/4)= 0.8112781244591328

2）Hot

Day	Outlook	Temp.	Humidity	Wind	Decision
3	Overcast	Hot	High	Weak	Yes
13	Overcast	Hot	Normal	Weak	Yes
1	Sunny	Hot	High	Weak	No
2	Sunny	Hot	High	Strong	No

Temp=Hot这个属性，一共有4个样本，2个Yes，2个No，计算熵如下：

Entropy(Decision|Temp=Hot) = -p(No)*log2p(No)-p(Yes)*log2p(Yes)= -(2/4)*log2(2/4)-(2/4) *log2(2/4)= 1.0

3）Mild

Day	Outlook	Temp.	Humidity	Wind	Decision
4	Rain	Mild	High	Weak	Yes
10	Rain	Mild	Normal	Weak	Yes
11	Sunny	Mild	Normal	Strong	Yes
12	Overcast	Mild	High	Strong	Yes
8	Sunny	Mild	High	Weak	No
14	Rain	Mild	High	Strong	No

Temp=Mild这个属性，一共有6个样本，4个Yes，2个No，计算熵如下：

Entropy(Decision|Temp=Mild) = -p(No)*log2p(No)-p(Yes)*log2p(Yes)= -(4/6)*log2(4/6)-(2/6)*log2(2/6)= 0.9182958340544896

4）汇总计算

Temp	Yes	No	样本数
Cool	3	1	4
Hot	2	2	4
Mild	4	2	6

通过统计数据可以看到，Cool占比4/14，Hot占比4/14，Mild占比6/14，加权上面的熵，得到下面的计算：

Gain(Decision,Temp.) = Entropy(Decision)  –[p(Decision|Temp.=Cool)*Entropy(Decision|Temp.=Cool)]  –[p(Decision|Temp.=Hot)*Entropy(Decision|Temp.=Hot)   –[p(Decision|Temp.=Mild)*Entropy(Decision|Temp.=Mild)] = 0.940-(4/14)*0.8112-(4/14)*1.0-(6/14)*0.9182= 0.029000000000000026

通过上面的计算，得到Outlook这个特征的信息增益为：Gain(Decision, Temp) = 0.029，又完成了一个，我们接着算下面一个一个特征Humidity 的条件熵。

4、Humidity 特征条件熵

Humidity	Yes	No	样本数
High	3	4	7
Normal	6	1	7

1）High属性的熵

Day	Outlook	Temp.	Humidity	Wind	Decision
3	Overcast	Hot	High	Weak	Yes
12	Overcast	Mild	High	Strong	Yes
4	Rain	Mild	High	Weak	Yes
1	Sunny	Hot	High	Weak	No
2	Sunny	Hot	High	Strong	No
14	Rain	Mild	High	Strong	No
8	Sunny	Mild	High	Weak	No

Humidity=High这个属性，一共有7个样本，3个Yes，4个No，计算熵如下：

Entropy(Decision|Humidity=High) = -p(No)*log2p(No)-p(Yes)*log2p(Yes)= -(4/7)*log2(4/7)-(3/7)*log2(3/7)= 0.9852281360342516

2）Normal属性的熵

Day	Outlook	Temp.	Humidity	Wind	Decision
7	Overcast	Cool	Normal	Strong	Yes
5	Rain	Cool	Normal	Weak	Yes
9	Sunny	Cool	Normal	Weak	Yes
13	Overcast	Hot	Normal	Weak	Yes
10	Rain	Mild	Normal	Weak	Yes
11	Sunny	Mild	Normal	Strong	Yes
6	Rain	Cool	Normal	Strong	No

Humidity=High这个属性，一共有7个样本，6个Yes，1个No，计算熵如下：

Entropy(Decision|Humidity=High) = -p(No)*log2p(No)-p(Yes)*log2p(Yes)= -(1/7)*log2(1/7)-(6/7)*log2(6/7)= 0.5916727785823275

5、汇总计算

Humidity	Yes	No	样本数
High	3	4	7
Normal	6	1	7

Gain(Decision,Humidity) = Entropy(Decision)  –[p(Decision|Humidity=High)*Entropy(Decision|Humidity=High)]  –[p(Decision|Humidity=Normal)*Entropy(Decision|Humidity=Normal) = 0.940-(7/14)*0.98522-(7/14)*0.5916= 0.15158999999999995

通过上面的计算，得到Humidity这个特征的信息增益为：Gain(Decision, Humidity) = 0.151 ，又完成了一个，我们接着算下面一个一个特征Humidity 的条件熵。

到此我们完成了所有特征的信息增益的计算，对所有特征进行排序，找增益最大的进行分列

排序后分裂

Feature	Gain	排名
Outlook	0.246	1
Temperature	0.029	4
Humidity	0.151	2
Wind	0.048	3

所以我们选择 outlook 这个特征作为第一次分裂特征，也是就决策树的根

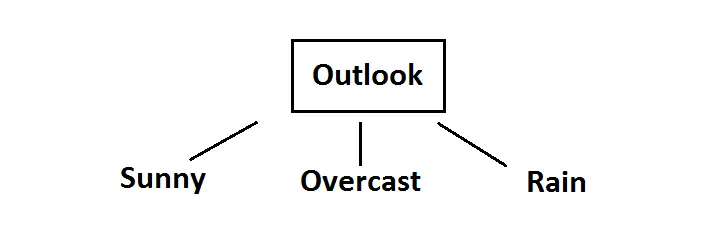Root decision on the tree

现在，我们需要进一步计算第二层的分裂特征的选择，在outlook分裂后的子集中计算。

第二层分裂决策

第一层分裂的特征决定了，那就要根据分裂的结果，进行第二层的分裂，同第一层，也是需要计算每个子集的经验熵 + 条件熵。

数据集第一步被Outlook 这个特征分裂成三个节点，现在需要对每个节点计算下一步的分裂特征。

1、Outlook -Overcast 节点

在overcast这个分支上，标签全部是yes，也就是已经彻底的完成了分裂了，这个就可以作为叶子节点，无需继续分裂。

Day	Outlook	Temp.	Humidity	Wind	Decision
3	Overcast	Hot	High	Weak	Yes
7	Overcast	Cool	Normal	Strong	Yes
12	Overcast	Mild	High	Strong	Yes
13	Overcast	Hot	Normal	Weak	Yes

无需继续分裂！！

2、Outlook-Sunny节点

在sunny 这个属性下面，还存在5个样本，包含3/5 的No, 2/5 的Yes，还需要继续分裂，所以这一层，我们重复上述的步骤，先计算这个子集的经验熵，然后计算每个特征的信息增益，找到最佳的分割特征。

Day	Outlook	Temp.	Humidity	Wind	Decision
1	Sunny	Hot	High	Weak	No
2	Sunny	Hot	High	Strong	No
8	Sunny	Mild	High	Weak	No
9	Sunny	Cool	Normal	Weak	Yes
11	Sunny	Mild	Normal	Strong	Yes

1）计算子集经验熵

首先我们计算Outlook=Sunny子集的经验熵

Entropy(Outlook=Sunny ) = -p(No)*log2p(No)-p(Yes)*log2p(Yes)= -(3/5)*log2(3/5)-(2/5) *log2(2/5) = 0.97095

下面计算每个特征的经验熵和信息增益。

2）Gain(Outlook=Sunny|Temp.)

Temp.	Yes	No	样本数
Hot	0	2	2
Cool	1	0	1
Mild	1	1	2

根据上面的统计数据，计算特征Temp.的条件熵

Entropy(Outlook=Sunny|Temp.) = 2/5*(-(0/2)*log2(0/2)-(2/2)*log2(2/2))+1/5*(-(1/1)*log2(1/1)-(0/1)*log2(0/1))+2/5*(-(1/2)*log2(1/2)-(1/2)*log2(1/2))= 0.4

计算得到Temp.特征的信息增益

Gain(Outlook=Sunny|Temp.) = Entropy(Outlook=Sunny)-Entropy(Outlook=Sunny|Temp.) = 0.97095-0.4 = 0.57095

根据上面的计算，可以得到最终的信息增益为：Gain(Outlook=Sunny|Temp.)=0.570

3）Gain(Outlook=Sunny|Humidity)

Humidity	Yes	No	样本数
High	0	3	3
Normal	2	0	2

根据上面的统计数据，计算特征Humidity的条件熵

Entropy(Outlook=Sunny|Humidity) = 3/5*(-(0/3)*log2(0/3)-(3/3)*log2(3/3))+2/5*(-(2/2)*log2(2/2)-(0/2)*log2(0/2))+= 0

计算得到Temp.特征的信息增益

Gain(Outlook=Sunny|Humidity) = Entropy(Outlook=Sunny)-Entropy(Outlook=Sunny|Humidity) = 0.97095-0 = 0.97095

4）Gain(Outlook=Sunny|Wind)

Wind	Yes	No	样本数
Weak	1	2	3
Strong	1	1	2

根据上面的统计数据，计算特征Temp.的条件熵

Entropy(Outlook=Sunny|Humidity) = 3/5*(-(1/3)*log2(1/3)-(2/3)*log2(2/3))+2/5*(-(1/2)*log2(1/2)-(1/2)*log2(1/2))+= 0.9509775004326937

计算得到Temp.特征的信息增益

Gain(Outlook=Sunny|Humidity) = Entropy(Outlook=Sunny)-Entropy(Outlook=Sunny|Humidity) = 0.97095-0.9509775004326937 = 0.01997249956730629

5）增益排序

Gain(Outlook=Sunny|Temp.)       = 0.570Gain(Outlook=Sunny|Humidity)    = 0.970Gain(Outlook=Sunny|Wind)        = 0.019

可以看到，humidity 是增益最高的，我们就按这个特征进行分裂，分裂结果如下，两个分支都是纯度百分百了

Day	Outlook	Temp.	Humidity	Wind	Decision
1	Sunny	Hot	High	Weak	No
2	Sunny	Hot	High	Strong	No
8	Sunny	Mild	High	Weak	No

On the other hand, decision will always be yes if humidity were normal

Day	Outlook	Temp.	Humidity	Wind	Decision
9	Sunny	Cool	Normal	Weak	Yes
11	Sunny	Mild	Normal	Strong	Yes

3、Outlook -Rain 节点

Day	Outlook	Temp.	Humidity	Wind	Decision
4	Rain	Mild	High	Weak	Yes
5	Rain	Cool	Normal	Weak	Yes
6	Rain	Cool	Normal	Strong	No
10	Rain	Mild	Normal	Weak	Yes
14	Rain	Mild	High	Strong	No

1）计算子集经验熵

我们计算Outlook=Rain子集的经验熵，在Outlook=Rain这个节点下，一共有5个样本，3个Yes，2个No，我们可以算出这个子集的经验熵。

Entropy(Outlook=Rain) = – p(No)*log2p(No)–p(Yes)*log2p(Yes)= - (2/5)*log2(2/5)-(3/5)*log2(3/5) = 0.97095

2）Gain(Outlook=Rain | Temp)

Temp.	Yes	No	样本数
Cool	1	1	2
Mild	2	1	3

根据上面的统计数据，可以计算出子集的熵

Entropy(Outlook=Rain|Temp) = 2/5*(-(1/2)*log2(1/2)-(1/2)*log2(1/2))+  3/5*(-(2/3)*log2(2/3)-(1/3)*log2(1/3))= 0.9509775

Gain(Outlook=Rain|Temp) = Entropy(Outlook=Rain)-Entropy(Outlook=Rain|Temperature) = 0.97095-0.9509775 = 0.01997

计算得到Temp特征的信息增益为：Gain(Outlook=Rain | Temp)=0.01997

3）Gain(Outlook=Rain | Humidity)

Humidity	Yes	No	样本数
High	1	1	2
Normal	2	1	3

根据上面的统计数据，可以计算出子集的熵

Entropy(Outlook=Rain|Humidity) = 2/5*(-(1/2)*log2(1/2)-(1/2)*log2(1/2))+\  3/5*(-(2/3)*log2(2/3) - (1/3) * log2(1/3))= 0.9509775
Gain(Outlook=Rain | Humidity) = Entropy(Outlook=Rain)-Entropy(Outlook=Rain|Temperature) = 0.97095-0.9509775 = 0.01997

计算得到Humidity特征的信息增益为：Gain(Outlook=Rain | Humidity)=0.01997，与上面的Temperature特征一样

4）Gain(Outlook=Rain | Wind)

Wind	Yes	No	样本数
Weak	3	0	3
Strong	0	2	2

根据上面的统计数据，可以计算出子集的熵

Entropy(Outlook=Rain|Wind) = 3/5*(-(0/3)*log2(0/3)-(3/3)*log2(3/3))+  2/5*(-(0/2)*log2(0/2)-(2/2) * log2(2/2))= 0
Gain(Outlook=Rain | Humidity) = Entropy(Outlook=Rain)-Entropy(Outlook=Rain|Wind) = 0.97095-0 = 0.97095

计算得到Wind特征的信息增益为：Gain(Outlook=Rain | Wind) =0.97095

综上，可以得到下面的结论，因此Wind的信息增益最大，选做本节点的分列特征

Gain(Outlook=Rain | Temperature) = 0.0199730940219748Gain(Outlook=Rain | Humidity)    = 0.0199730940219748Gain(Outlook=Rain | Wind)        = 0.9709505944546686

分列后得到下面两个叶子节点，叶子节点的纯度都为100%，也就是只有一个标签类型，因此无需继续分列。

Wind = Weak

Day	Outlook	Temp.	Humidity	Wind	Decision
4	Rain	Mild	High	Weak	Yes
5	Rain	Cool	Normal	Weak	Yes
10	Rain	Mild	Normal	Weak	Yes

Wind = Strong

Day	Outlook	Temp.	Humidity	Wind	Decision
6	Rain	Cool	Normal	Strong	No
14	Rain	Mild	High	Strong	No

五、决策树生成

综合第一、第二层的计算，我们得到了最终的决策树如下：

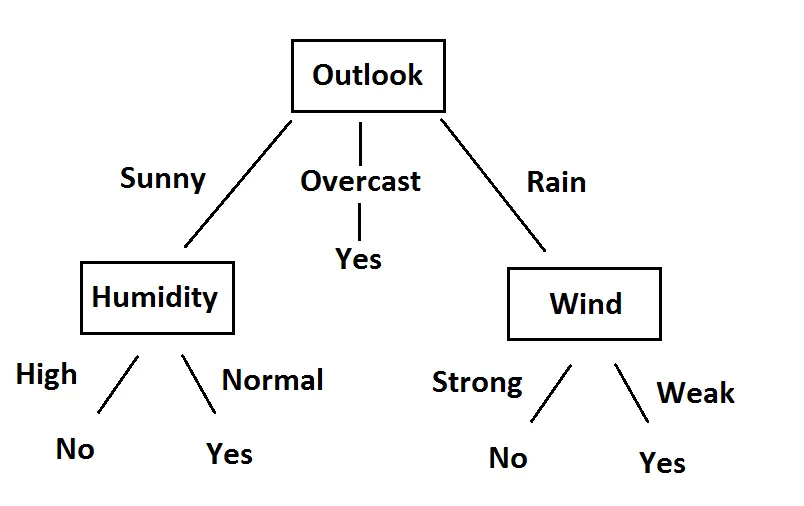
Final version of decision tree

一、Number（数字）
全面掌握Python基础，这一篇就够了，建议收藏
Python基础之数字（Number）超级详解
Python随机模块22个函数详解
Python数学math模块55个函数详解
二、String（字符串）
Python字符串的45个方法详解
Pandas向量化字符串操作
三、List（列表）
超级详解系列-Python列表全面解析
Python轻量级循环-列表推导式
四、Tuple（元组）
Python的元组，没想象的那么简单
五、Set（集合）
全面理解Python集合，17个方法全解，看完就够了
六、Dictionary（字典）
Python字典详解-超级完整版
七、内置函数
Python初学者必须吃透这69个内置函数！
八、正则模块
Python正则表达式入门到入魔
笔记 | 史上最全的正则表达式
八、系统操作
Python之shutil模块11个常用函数详解
Python之OS模块39个常用函数详解
九、进阶模块
【万字长文详解】Python库collections，让你击败99%的Pythoner
高手如何在Python中使用collections模块
【万字长文】详解Python时间处理模块-datetime

十、Pandas数据分析
Pandas中的宝藏函数-rank()
Pandas中的宝藏函数-transform()
Pandas中的宝藏函数-agg()
Pandas中的宝藏函数-apply
Pandas中的宝藏函数-map
Pandas中的宝藏函数-applymap
一网打尽Pandas中的各种索引 iloc,loc,ix,iat,at,直接索引
一文搞懂Pandas数据排序
Pandas向量化字符串操作
Pandas缺失值处理-判断和删除
Pandas一行代码绘制26种美图
Pandas数据可视化原来也这么厉害
↓扫描关注本号↓

深刻理解决策树-动手计算ID3算法

二、数据集介绍

三、经验熵计算

四、条件熵计算

第一层分裂决策

1、Wind条件熵

2、Outlook 条件熵

3、Temp 特征的条件熵

4、Humidity 特征条件熵

5、汇总计算

第二层分裂决策

1、Outlook -Overcast 节点

2、Outlook-Sunny节点

3、Outlook -Rain 节点

五、决策树生成