决策树算法
转自:Alrange公众号
你可能做过这样的选择:
选择考研学校时,如果这是一个普通学校,你不会选择该学校。
但如果这是一个好的一本学校,你选择继续了解它。
并且如果它地理位置不错,在你喜欢的城市,你选择继续了解它。
并且如果你选择的专业在该校很出名,你选择继续了解它。
接下来你发现你的能力水平也可以到达这个目标,那么你直接选择报考它。
相反,如果你的能力水平不能达到,那么你不会选择该学校。
把你上面的一系列决策分支画下来,就形成了一颗下面的决策树。
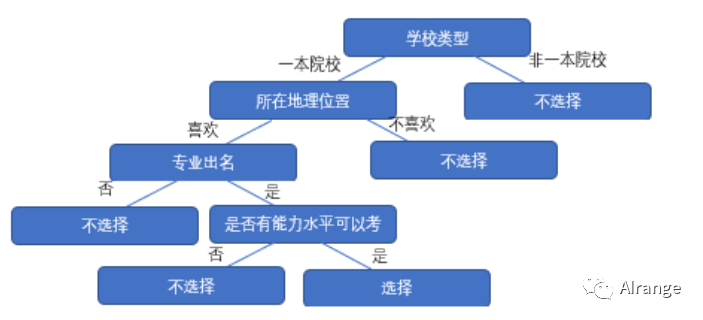
这样的决策思路可以用到我们的机器学习中的分类来,这个算法就叫作决策树。
本文涉及到的内容:
1、什么是决策树
2、决策树的三种算法
3、决策树的实例应用
4、决策树的算法补充
什么是决策树
原理
假设现在有两类物体,他们各有两种特征,投影到二维空间上后,如下图所示:
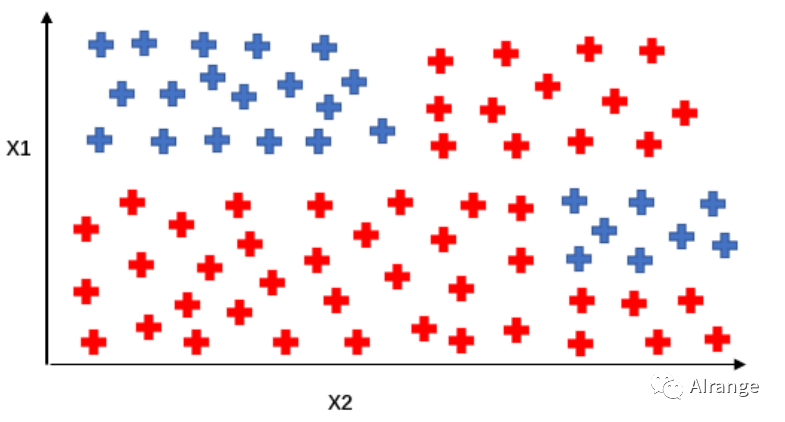
我们想要在几次操作后把两种种类分开来,于是就有了下面的划分方法。
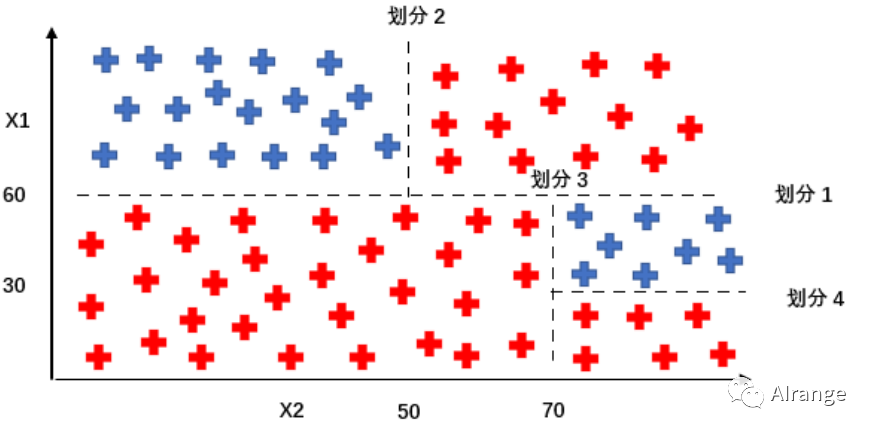
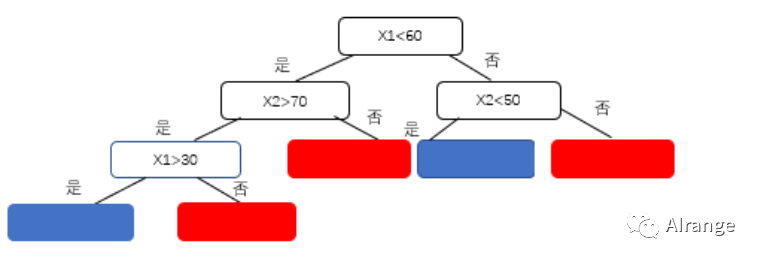
可以看到,这样的划分方法实质是利用训练集构造了这样的决策树,之后这个决策树可以用于分类测试的样例。
概念
决策树是最经常被使用于分类问题的监督学习算法,并且可以用于类别型特征和连续型特征。
一个决策树它的每个分支节点都代表在一些不同选择中的一个选择,并且每一个叶子都代表最终的一个决策。
构造这个决策树会用到许多不同的算法,将会从这些历史数据中建立一个决策树,并且这个生成的决策树可以分类未来遇到的样例。
那么树的构造算法有哪些呢?结点是如何分裂的呢?
算法介绍
ID3
它的基本思想是采用从顶向下的贪心算法,以信息增益为准则来产生结点。
我们先来了解两个公式:
①熵
熵在机器学习中的意义和在热力学中的意义相同,是测量随机性的方法。
在这里我们用它来表示样本集合的纯度,公式如下。
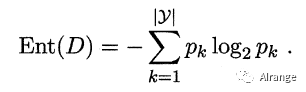
其中,pk是第k类样本在样本集合D中所占的比例。|y|是样本的类别个数。
②信息增益
为属性a对样本集D进行划分后所获得的“信息增益”。信息增益表示得知属性A的信息而使得样本集合不确定度减少的程度,公式如下。
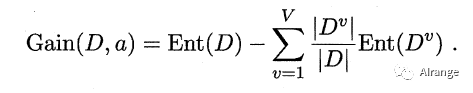
V是离散属性a可能取值的个数。带标号v的D是D中属性值a=v的样本集合。
选择最优属性就是是它可以给出最大的信息增益。
明白了这两个概念之后,我们就可以来看构造树的步骤。
③步骤
1、计算数据集的熵。(即根节点的信息熵)
2、对每一个属性/特征:
①计算所有分类值的熵。②对该属性取一个平均信息熵。③计算该属性的信息增益。
3、选择具有最高的信息增益的属性作为下一个树节点。
4、重复以上操作直到我们得到期望的树。
C4.5
可以发现,如果一个属性的取值数目较多的话,它信息增益也会相应的变大,那么就会每次分裂使偏向选择取值数目多的属性,为了避免这种情况,接下来讲到的C4.5算法,对ID3做了改进。
此算法的思想是用信息增益除以一个属性的固有值,可以一定程度地避免选择分类多的属性,漏掉了一些好的特征。
首先看信息增益率的公式:
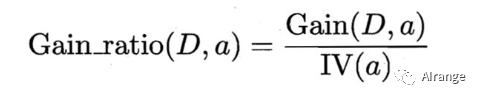
IV(a)的公式,即属性a的一个固有值:
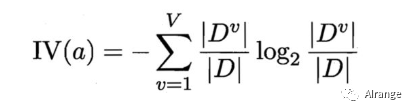
由公式可以反映出,当选取该属性,该属性的可取值数越大,IV(a)就越大。
但是C4.5算法不直接选择增益率最大的候选划分属性,它会在候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的,原因是避免选择属性取值数目小的属性。
CART算法
CART是一颗二叉树,它可以是分类树也可以是回归树。
采用GINI值作为节点分裂的依据.。
GINI值的计算公式:
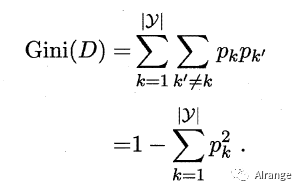
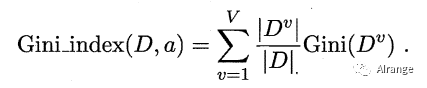
我们在候选属性集合A中,选择那个使得划分后基尼指数最小的属性作为最优划分属性。
实例
我们调用sklearn里面的决策树方法来预测用户是否购买汽车的意愿。
数据的预处理在之前的文章内容提到过,没看过的同学可以戳文末的链接~
那么直接调用决策树分类器:
1from sklearn.tree import DecisionTreeClassifier
2classifier = DecisionTreeClassifier(criterion = 'gini',max_depth=3)#这里设置划分准则为gini,树的最大深度是3.
3classifier.fit(X_train, y_train)
4y_pred = classifier1.predict(X_test)
接下来用混淆矩阵查看预测结果:
1from sklearn.metrics import confusion_matrix
2cm = confusion_matrix(y_test, y_pred)
3cm
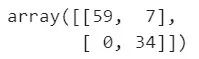
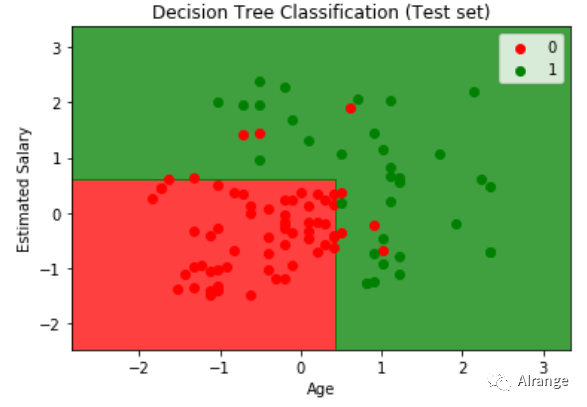
我们还可以可视化结果,来查看决策树的决策边界:
1from matplotlib.colors import ListedColormap
2X_set, y_set = X_test, y_test
3X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
4 np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
5plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
6 alpha = 0.75, cmap = ListedColormap(('red', 'green')))#画出决策树的决策边界
7plt.xlim(X1.min(), X1.max())#设置坐标范围
8plt.ylim(X2.min(), X2.max())
9for i, j in enumerate(np.unique(y_set)):#将测试集以散点形式画出
10 plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
11 c = ListedColormap(('red', 'green'))(i), label = j)
12plt.title('Decision Tree Classification (Test set)')#设置标题
13plt.xlabel('Age')
14plt.ylabel('Estimated Salary')
15plt.legend()
16plt.show()
决策树算法步骤
这里补充了一个内容,是较为详细的决策树的基本算法,它采用递归调用的方法,算法中共有三次返回(Return)的情况。

感兴趣的同学可以阅读。
参考资料:
https://github.com/Avik-Jain/100-Days-Of-ML-Code
机器学习——周志华
