【机器学习】用摸鱼学来解释隐马尔可夫模型(HMM)

假如小明一周工作六天,每天工作状态都不相同,比如有活少、活多、心情好、心情差和双倍工资5种状态,不同工作状态下工作效率也不相同,活少和心情差的时候摸鱼时间多,活多、心情好和双倍工资的时候摸鱼时间少。
从小明的工作日常中可以提炼出5种状态和2种观测和观测6天。
状态:活少、活多、心情好、心情不好、双倍工资
观测:摸鱼、认真上班
将涉及到的可能情况展开如下图所示。
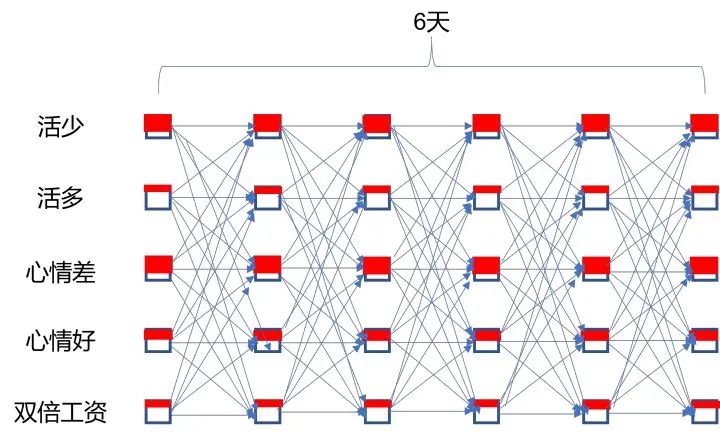
每一行对应相同状态,每一列对应每一天。其中红色块在矩形中的占比表示一天中摸鱼的程度,也就是摸鱼的观测概率。蓝色箭头表示不同状态间的转移概率。那么状态序列总共有5^6种。
假设天数为T(列数),状态数为N(行数)。
问题1(概率计算问题):假如观察小明的六天,得到的观测序列为:摸鱼 -> 认真工作 -> 摸鱼 -> 认真工作 -> 摸鱼 -> 认真工作,并且已知蓝色箭头的状态转移概率和摸鱼的观测概率,请问该观测序列的概率为多少?
从上图就可以知道只要求出所有能够得到该观测序列的状态序列概率之和就行了。总共有N^T种状态序列(穷举所有蓝色箭头路径),并且每种状态序列需要T个观测概率相乘(每个状态一个观测概率),所以总的计算复杂度为O(N^T)。这种暴力求解的方法计算复杂度太高了,可以用前向-后向算法来减少计算量。
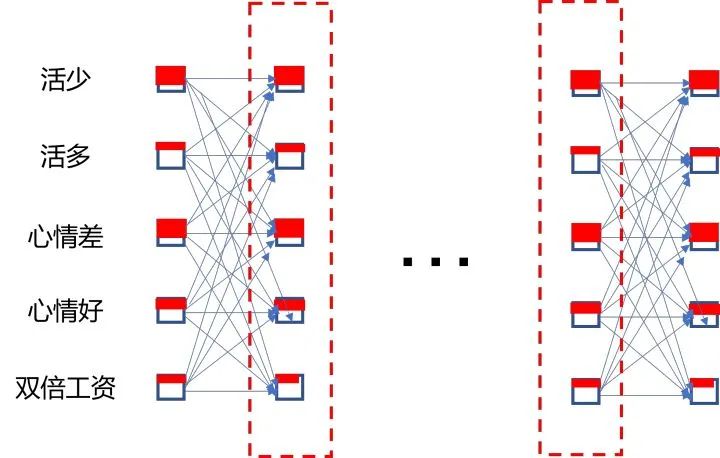
以前向算法为例(后向算法可以认为是状态序列的反转,计算方法相同),简单来说,就是利用分治和动态规划的思想,把6天拆分成5个重复单元,然后先计算出第一个重复单元红色虚线框中每个状态的观测概率,并且保存下来当作下一个重复单元的初始状态,循环5次就得了最终的观测概率。每个重复单元总共有N^2种状态序列,并且每种状态序列需要2个观测概率相乘,所以一个重复单元的计算复杂度为O(N^2),那么总的计算复杂度为O(TN^2)。比起暴力求解观测概率,复杂度大大降低。
问题2(学习问题):已知小明加上同事,总共有10人的观测序列,请问如何估计不同状态之间的转移概率和摸鱼的观测概率呢?
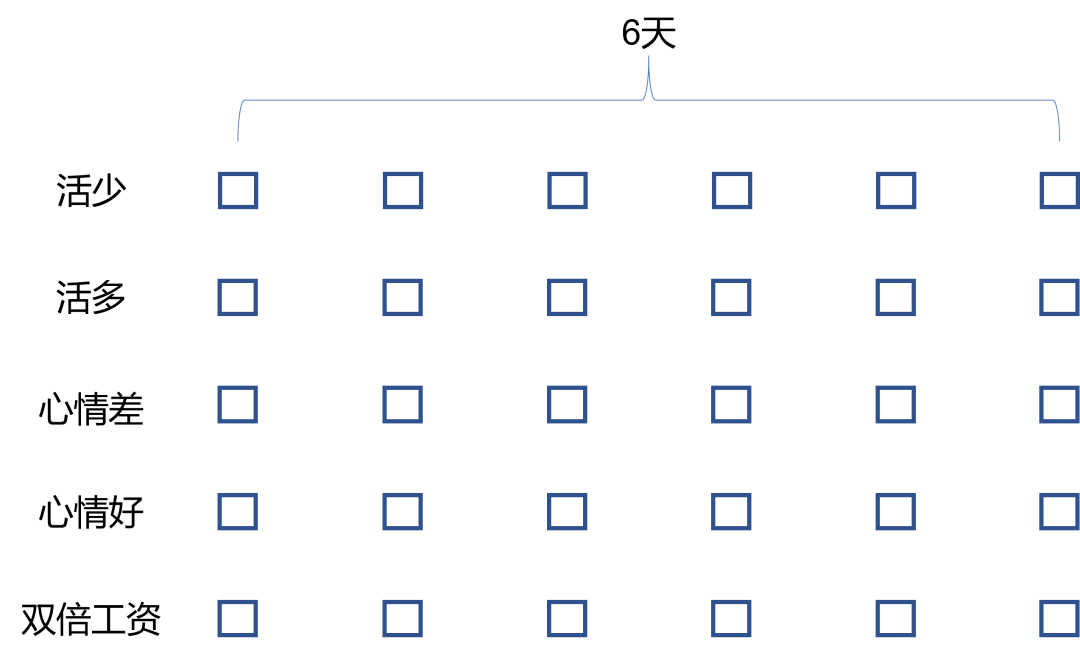
如图所示,红色块和蓝色箭头是需要通过10人的观测序列估计出来的。这里需要用到Baum-Welch算法,简单来说,就是通过EM算法构建出带隐函数的优化函数Q,然后用拉格朗日函数求解。
问题3(预测问题):假如观察小明的六天,得到的观测序列为:摸鱼 -> 认真工作 -> 摸鱼 -> 认真工作 -> 摸鱼 -> 认真工作,并且已知蓝色箭头的状态转移概率和摸鱼的观测概率,请问该观测序列最有可能的状态序列是什么?
这个问题跟问题1很相似,不同的地方在于问题1是求该观测序列的所有状态序列概率之和,而问题3求的是该观测序列的所有状态序列中最有可能出现的状态序列。
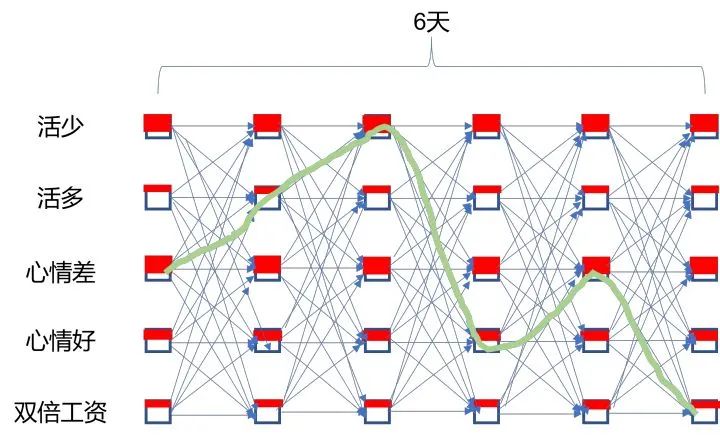
所以求解方式和问题1类似,只不过需要从所有可能状态序列中找出概率最大的状态序列。上图绿色路径可能就是概率最大的状态序列。
可见隐马尔可夫模型简直太有用了!老板可以通过公司的规章制度来引导员工的身心健康!或者根据员工的摸鱼情况来预测员工的身心健康,从而更好的优化公司的规章制度!


往期精彩回顾 本站qq群851320808,加入微信群请扫码:
