∇SLAM：自动可微分SLAM-技术圈

点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达

摘要

将表示学习方法与同时定位和建图(SLAM)系统相结合是一个开放的问题,因为它们的高度模块化和复杂性.在功能上,SLAM是一种将原始传感器输入转换成机器人和环境状态分布的操作.如果这种转换(SLAM)可以表达为一个可微函数,我们可以利用基于任务的错误信号来学习优化任务性能的表示.然而,典型的稠密SLAM系统的几个组件是不可区分的.在这项工作中,我们提出了∇SLAM(gradSLAM),一种方法提出SLAM系统作为可微分的计算图,它统一了基于梯度的学习和SLAM.我们提出了可区分的信赖域优化器、表面测量和融合方案以及光线投射,而不牺牲精度.这种稠密的SLAM与计算图形的融合使我们能够从3D地图一路回溯到2D像素,为基于梯度的SLAM学习开辟了新的可能性.

引言

同步定位和建图(SLAM)几十年来一直是机器人感知和状态估计的核心问题.SLAM文献的很大一部分直接或间接地集中在地图表示的问题上.最近，基于梯度的学习方法已经改变了几个领域的前景(例如图像识别，语言建模，语音识别).然而,这种技术在SLAM中的成功有限,从形式上来说,我们需要一个将图像中的像素(或者一般来说，传感器测量值)与环境的3D地图M相关联的表达式.我们建议通过开发一个可微映射函数来解决这个问题.那么映射∇sM的梯度可以直观地告诉我们,用无穷小的δs扰动传感器测量值s会导致映射m被

改变.

实现完全可微的SLAM系统的核心目标是计算图,这是大多数基于梯度的学习技术的基础.我们观察到,如果一个完整的SLAM系统可以分解成所有可微的基本运算,我们可以组合这些基本运算来保持可微性.然而现代稠密的SLAM系统相当复杂,这使得开发这样系统具有挑战性.

我们提出了∇SLAM (gradSLAM),SLAM的一个可微的计算图视图.我们展示了SLAM中所有不可微函数是如何实现为光滑映射的.∇SLAM框架是非常通用的,并且可以扩展到大多数稠密SLAM系统的可微性.

为了促进对可区分SLAM系统及其在空间基础学习中的应用的进一步研究,∇SLAM提供了一个开源PyTorch框架.

官方Demo如下:

项目页面和代码如下:

https://gradslam.github.io

实验和结果

1 可微优化

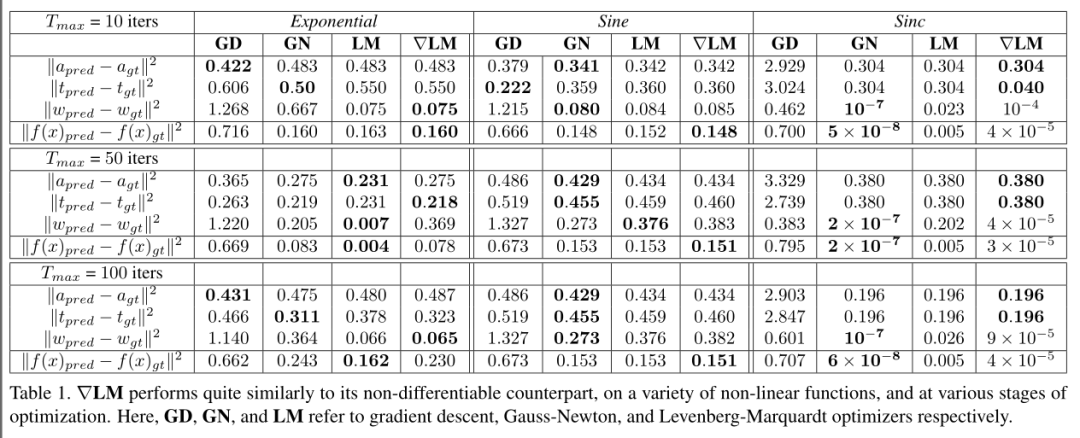
在前文中,我们引入了两个广义逻辑函数来计算阻尼函数以及随后的迭代.我们进行了多个实验来验证这种近似对非线性最小二乘解算器的性能(收敛速度、解的质量)的影响.

我们首先设计了几个问题(来自[5]的启发),来衡量∇LM相对于其不可微的对手的表现.我们考虑三个非线性函数,即指数、sine和sinc,各有三个参数a、t和w.

对于这些函数中的每一个,我们对参数p = {a，t，w}进行统一采样,以创建一组基本事实曲线,并对区间[6，6]中的初始猜测p0= {a0，t0，w0}进行统一采样.我们为三个函数中的每一个函数抽取了100个问题实例.我们运行各种优化器(如梯度下降(GD)、高斯-牛顿(GN)、LM和∇LM)进行最多10、50和100次迭代.我们计算参数空间(独立于每个参数a、t、w)和函数空间中的均方误差.请注意,这两个误差不一定线性相关,因为参数和函数变量之间的相互作用是高度非线性的.结果见表4.3,可以看出,∇LM的表现与LM几乎相同.

2 案例研究的比较分析

我们将Kinect-Fusion、PointFusion和ICP-SLAM实现为可微分计算图.在这里,我们分析了每种方法与其不可微的对应方法的比较.表2显示了ICP-SLAM和点融合的不可微和可微(∇)版本的轨迹跟踪性能.当利用可微分建图模块和∇LM进行优化时,我们没有观察到性能的实际变化.这是在起居室序列的分割子集上计算的.

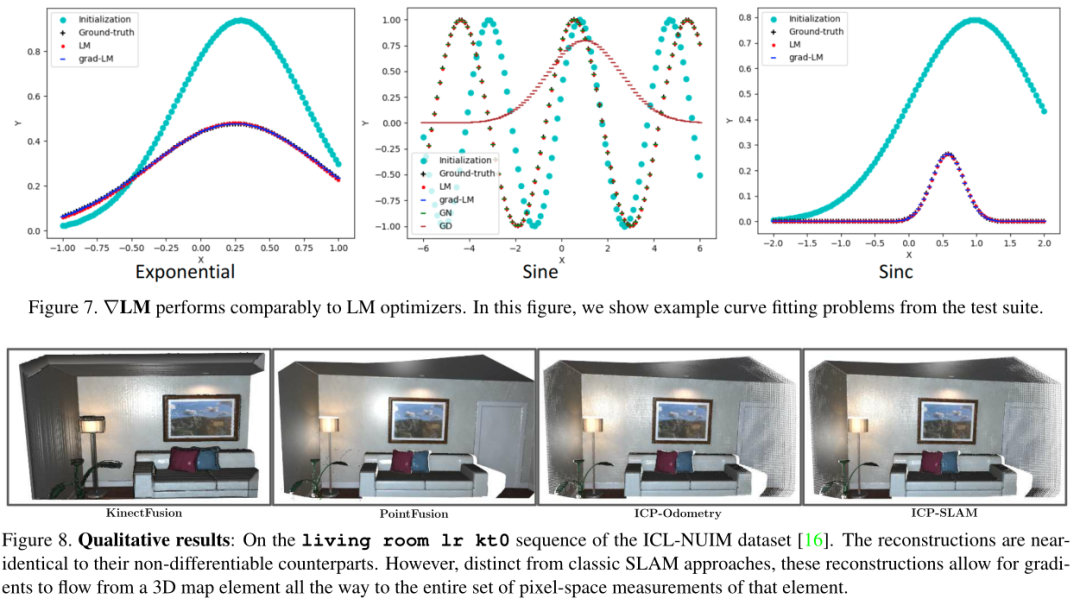
我们还用kincontinuous的重建质量来评价∇KinectFusion的重建质量.在ICLNUIM 基准的living_room_traj0序列的一个子段上,Kintinuous的表面重建质量为18.625,而可微KinectFusion的表面重建质量为21.301(更好).然而,这个量是误导性的,因为Kintinuous在提取的网格中只保留了高置信度点的子集,而我们的可微分KinectFusion输出(见图8)包含一些噪声伪像,这是由于我们的平滑截断函数.

3 定性结果

∇SLAM在多个其他RGBD数据集上工作.具体而言,我们展示了在TUM RGB-D数据集等以及在从英特尔RealSense D435相机捕获的内部序列上运行可区分SLAM系统的定性结果.

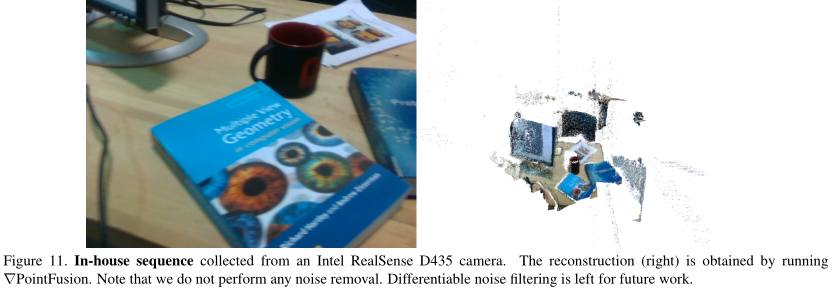
图9- 11显示了通过对来自TUM RGB等各种序列进行∇SLAM分析获得的定性结果.这些可区分的SLAM系统都完全在图形处理器上执行,并且能够计算关于任何中间变量的梯度(例如相机姿态、像素强度/深度、优化参数、相机固有特性等).

4 梯度分析

∇SLAM的计算图形方法允许我们恢复关于3D表面重建的2D(或2.5D)测量的有意义的梯度.在图12中,最上面一行示出了可微分变换的RGB-D图像—使用∇SLAM(有噪声的)TSDF表面测量,然后与更精确的全局TSDF图进行比较.对齐体积的元素比较给我们一个重建误差,它的梯度使用由∇SLAM维护的计算图(并在深度图像空间中可视化)反向传播到输入深度图.在第二行中,我们有意引入一个mask来遮挡RGB-D图像中的一个小区域(40 × 40),从而引入一个重建伪影.计算体积误差在全局和局部遮挡TSDF体积之间,检查相对于输入的梯度指示遮挡表面对体积误差的每像素贡献.因此,∇SLAM提供了计算梯度的丰富解释:它们表示每个像素对最终三维重建的贡献.

5 应用

在图13中,我们类似地在一个深度中引入这种限流器(顶行)和像素噪声(底行)使用∇PointFusion.重建场景. 然后,我们计算噪声表面图和真实表面图之间的倒角距离,并对每个像素的误差进行反向传播.最小化的损失导致噪声和遮挡区域的目标恢复.我们另外在图14中示出了一个RGB-D图像完成任务(来自均匀噪声).

结论

我们引入了∇SLAM,一个可区分的计算图框架,它通过提供关于输入图像和深度图的明确梯度,为大量基于定位和建图的任务实现了基于梯度的学习.我们展示了一系列不同的案例研究,并展示了梯度在跟踪、建图和融合阶段的表现.

下载1：OpenCV-Contrib扩展模块中文版教程

在「小白学视觉」公众号后台回复：扩展模块中文教程，即可下载全网第一份OpenCV扩展模块教程中文版，涵盖扩展模块安装、SFM算法、立体视觉、目标跟踪、生物视觉、超分辨率处理等二十多章内容。

下载2：Python视觉实战项目31讲

在「小白学视觉」公众号后台回复：Python视觉实战项目31讲，即可下载包括图像分割、口罩检测、车道线检测、车辆计数、添加眼线、车牌识别、字符识别、情绪检测、文本内容提取、面部识别等31个视觉实战项目，助力快速学校计算机视觉。

下载3：OpenCV实战项目20讲

在「小白学视觉」公众号后台回复：OpenCV实战项目20讲，即可下载含有20个基于OpenCV实现20个实战项目，实现OpenCV学习进阶。

下载4：leetcode算法开源书

在「小白学视觉」公众号后台回复：leetcode，即可下载。每题都 runtime beats 100% 的开源好书，你值得拥有！

交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~