SLAM基础：相机与图像

来自 | 知乎   

链接丨https://zhuanlan.zhihu.com/p/33583981

本文仅作学术交流，如有侵权，请联系后台删除。

相机拍照，是将三维世界中的一个三维点映射到对应的二维影像平面的过程。这个过程能够用一个几何模型来进行描述。在各种各样的模型中，最简单也最常用的就是针孔相机模型，也叫针孔模型。这个模型较为简单，而由于相机镜头上透镜的存在，成像的过程中会有畸变产生。为此，需要另外对畸变进行建模。

 

针孔相机模型

初中物理里都会有一个小孔成像的实验，这个小孔成像的模型可以看作是针孔相机模型的基础。

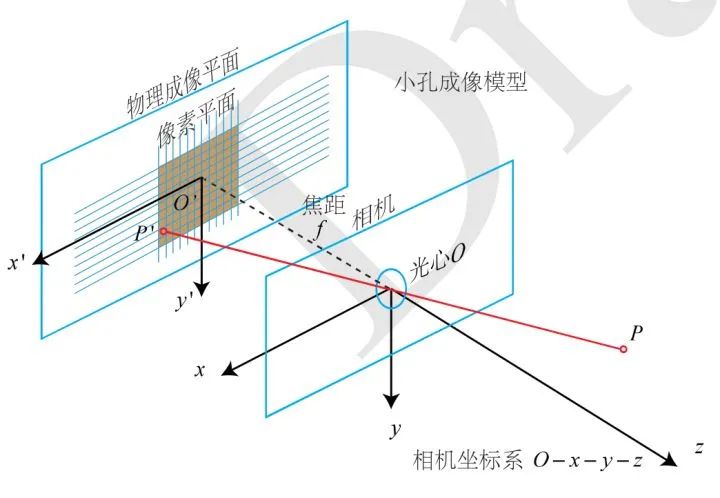
如上图所示，相机坐标系为O-x-y-z，想象人站在相机后面，O 为相机光心，z轴指向相机前方，x 轴向右而y 轴向下。真实世界中的一个点P，经过小孔O 投影后，落在物理成像平面O'-x'-y' （也称像平面坐标系）上，称为像点P'。

假设P在相机坐标系下的坐标为[X, Y, Z]T，P' 为[X', Y', Z']T，焦距为f。根据相似三角形有：

其中，负号表示所成的像是倒立的。

习惯上把成像平面对称到相机的前方，再整理一下上式即可得：

至此，我们描述了点P 和它的像之间的空间关系。在数码相机中，我们最终得到的是由一个个像素组成的数字影像，这需要在成像平面上进行采样和量化。这里就不针对二者进行介绍了。

在物理成像平面上定义一个像素坐标系 o'-u-v。一样地想象人站在相机之后，其原点o' 位于图像的左上角，u轴向右和x 轴平行，v 轴向下和y 轴平行。假设P' 的像素坐标为[u, v]T。像素坐标系和物理成像平面O'-x'-y' 之间相差缩放和平移。因此，假设像素坐标在u轴上缩放了 倍，在v 轴上缩放 倍。同事，二者之间的平移量为[cx, cy]T。那么，P' 在物理成像平面下的坐标和其像素坐标间的关系为：

将式(2) 代入并把  合并成  ，把  合并成 （这也是x 轴上的焦距和y 轴上的焦距不同的原因），可得：

上式就是相机坐标系下，一个空间点的三维坐标到其对应像点到像素坐标到转换关系。其中，f 的单位为米，  的单位为像素/米。

利用齐次坐标，将上市写成矩阵形式可得：

上式中，K 称为相机矩阵或者内参数矩阵，因为它包含的都是相机的参数。一般习惯把Z 放在左侧，计算完后再对结果除以其第三个值以得到像素坐标。通常认为相机矩阵在出厂之后是固定的并由厂家给出。如果没有则可以对相机进行标定以得到相机内参。

注意一直到这里，我们都没有涉及到相机的位姿T，因为我们一直在相机坐标系下。相机的位姿描述了相机在世界坐标系下的位置和姿态，也给出了世界坐标系到相机坐标系的变换关系。举例来说，对于一组照片，如果取第一张照片对应的相机坐标系为世界坐标系，则对应的相机位姿为旋转矩阵为单位阵而平移向量为0。而其他照片对应的相机位姿为该世界坐标系下到该照片对应的相机坐标系的变换关系。

由于相机在运动，所以点P 的相机坐标应该是它的世界坐标，记作Pw，根据相机当前的位姿变换到相机坐标系下的结果。

上式使用了齐次坐标并且包含了一次齐次坐标到非齐次坐标的变换。其中，R，t 或着T 表示相机的外参数，它会随着相机的运动而发生改变，是SLAM 过程中待估计的目标，表示着机器人的轨迹。最后，上式的T 为Tcw，表示世界坐标系到相机坐标系的变换，其转置为Twc。

注意到齐次坐标乘上一个非零常数后表示的是同一个点，所以可以把上市左侧中的Z 去掉。

前面我们提到这个式子包含一次齐次坐标到非齐次坐标的变换。因为右侧的TPw 是一个4维向量。将之除以最后一维并取前三维得到相机坐标系下的三维坐标。对于这个三维向量，按照齐次坐标的方式，可以再对其最后一维进行归一化处理，就得到了P 在相机归一化平面 上的投影：

此时，Pc 可以看成是一个二维的齐次坐标，称为归一化坐标。它可以看成是位于相机前方z = 1 处的平面上，该平面称为归一化平面。Pc 经过相机内参后就得到了像素坐标，所以可以把像素坐标[u, v]T 看成是归一化平面上的点进行量化测量的结果。

这一小节我们介绍了相机模型和各个坐标系的转换关系。其中涉及了世界坐标系，相机坐标系，归一化坐标，像平面坐标系和像素坐标系。要注意它们之间的区别和两两之间的转换关系。

畸变

为了获得好的成像效果，一般会在相机前方加上各种透镜。这就会对光线的传播产生新的影响：

• 透镜自身对光线传播的影响；

• 由于机械组装中的误差，导致透镜和称像平面不完全平行而产生的误差。

第一种原因引起的畸变称为径向畸变。因为在实际的加工过程中，透镜一般是中心对称的，这就使得这种畸变通常也是径向对称。它主要分为两大类：桶形畸变和枕形畸变。

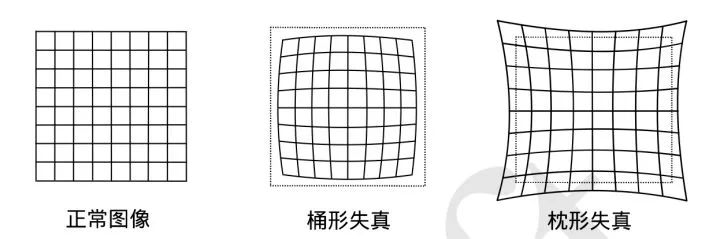
可以看大，桶形畸变是由图像的放大率随着光轴之间的距离增加而减小；枕形畸变则相反。它们是径向畸变，因此穿过图像中心和光轴有交点的直线能保持形状不变。

而第二种原因引入的畸变称为切向畸变，并不存在对称性质。

前面说过，假设某一点P的归一化表示为[x, y]T。也可以用极坐标来表示它，写作  . 径向畸变可以看作是坐标点沿着长度方向发生了变化  ，也就是其距离原点的长度发生了变化；切向畸变可以看成是坐标点沿着切线方向发生了变化，也就是水平夹角变化了  。

对于径向畸变，由于它们都是随着与中心之间的距离增加而增加，因此可以用一个多项式函数来描述畸变前后的坐标变化：

在上式中，对于畸变较小的图像中心区域，畸变纠正主要是k1 起作用；对于畸变较大的边缘区域，主要是k2 起作用。根据所用镜头，可以适当使用合适的校正系数。

对于切向畸变，可以使用另外的两个参数p1, p2 来进行纠正：

联合上面两个式子，对于相机坐标系中的一点P [X, Y, Z]，找到其对应像点的像素坐标的过程可以描述为：

1. 将三维空间点投影到归一化图像平面。设它的归一化坐标为[x, y]T;

2. 进行畸变矫正：

3. 通过相机的内参数，利用纠正后的点求的该点的像素坐标：

 

双目相机模型

针孔相机模型描述了单个相机的成像过程。但仅有一张相片是不足以确定对应空间点的具体位置的。考虑相机光心O 和像点p，二者的连线在物方空间是一条射线，这条射线上的所有点都可能投影到这个像点上。只有当P的深度确定时，才能确定它的空间位置。

确定深度的方法有很多种，人眼就是一个典型的双目相机模型：通过左右眼看到的景物的差异（称为视差）来判断物体与我们之间的距离。利用双目相机，同时采集左右相机的图像，计算图像间的时差，以此估计每一个像素的深度。

双目相机一般由左右两个相机组成，可以把两者都看作是针孔相机。左右相机间的距离称为基线（一般二者严格平行，距离固定）。

考虑一个空间点P，它在左右相机上的像点分别为Pl, Pr。在理想情况下，这两个像的位置的差异只出现在x 轴上（因为左右相机严格平行，只在x 轴上有差异）。记左右像点的x 轴上的像素坐标分别为uL, uR。根据下图所示的相似三角形有：

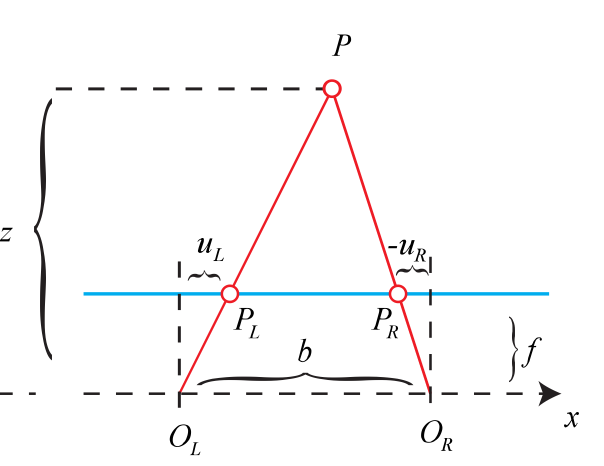
设  为左右像点的横坐标之差，即视差。根据上市则有：

可以看到，视差与距离成反比。时差越大，距离越近。此外，基线d 确定了双目相机能确定的深度的最大值。基线越长，能测得的距离就越远。

RGB-D 相机模型

RGB-D 相机可以主动测量每个像素的深度。目前的RGB-D 相机按原理可以分为两大类：

1. 通过红外结构光 来测量像素深度，如Kinect 1;

2. 通过飞行时间 (time-of-flight) 来测量像素深度，如Kinect 2.

测量了深度后，RGB-D 相机通常按照（生产时就确定好的）相机摆放位置，自动完成深度图和彩色图之间的配对工作，输出一一对应的彩色图和深度图。如此，我们就可以在两张影像上的同一个像素位置读取到色彩信息和深度信息，计算像素的三维坐标。

图像

在计算机中，图像是一个二维数组/ 矩阵。以最简单的灰度图为例，每个像素位置(x, y) 对应一个灰度值I。则一个宽为w 高为h 的图像可以表示为：

由于存储空间和数值精度的限制，我们无法表达出所有色彩。常用0 - 255 的整数（即一个字节）来表达图像的灰度强度。则一张宽640 高480 像素分辨率的灰度图就表示为：

unsigned char image[480][640]

注意到高度为图像的行数而宽度则为列数。而计算机中第一个下标为数组的行，第二个下标为数组的列。表示为：

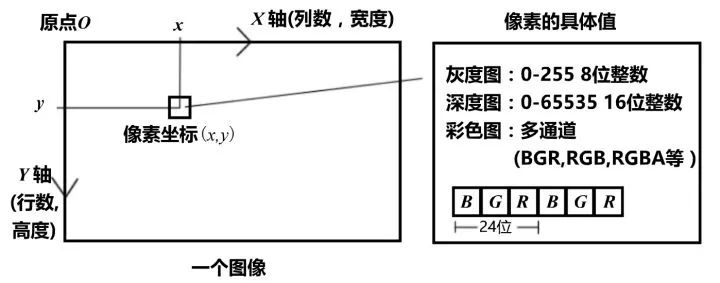
注意到这里y 轴是行而x 轴是列。所以如果我们想访问像素坐标为 (x, y) 的像素，则应写为：

 unsigned char pixel = image[y][x]

请读者注意这里x 和y 的顺序。这是很多程序错误的原因。

彩色图像由于在一个位置上同时有RGB 分别对应的像素强度，所以引入了通道 (channel) 的概念。对于每一个像素，用三个通道分别保留其R、G、B 上的像素值。和灰度图一样，每个通道一般也是一个字节（8位），彩色图的一个像素需要24 位存储空间。

对于RGB-D 相机产生的深度图，距离单位一般为毫米，8 位存储空间只能表示0.255 米，显然是不够的。一般采用16位整数来记录深度图的信息。16位整数能表示0 - 65535 之间的数值，最大值大概为65米。从这里我们也可以看出，RGB-D 相机不能表示大范围的距离信息。