【图神经网络】基于GNN的不同变种及其应用
图神经网络
图神经网络(Graph Neural Network,GNN)最早由 Scarselli 等人提出。图中的一个节点可以通过其特征和相关节点进行定义,GNN 的目标是学习一个状态嵌入 用于表示每个节点的邻居信息。状态嵌入 可以生成输出向量 用于作为预测节点标签的分布等。
下面三张图分别从图的类型,训练方法和传播过程角度列举了不同 GNN 的变种。


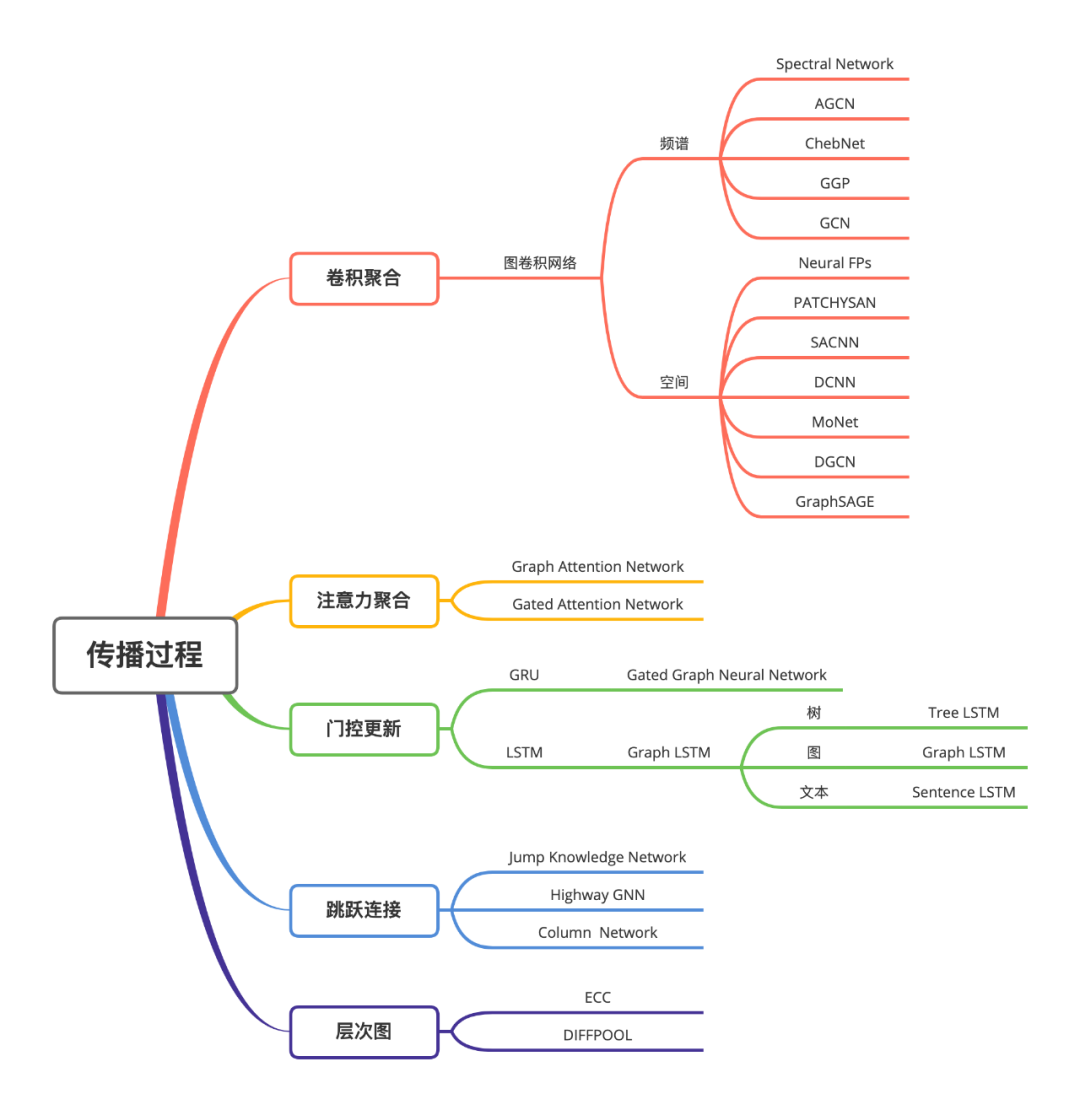
下面我们主要从模型的角度分别介绍不同种类的 GNN。
Graph Neural Networks
为了根据邻居更新节点的状态,定义一个用于所有节点的函数 ,称之为 local transition function。定义一个函数 ,用于生成节点的输出,称之为 local output function。有:
其中, 表示输入特征, 表示隐含状态。 为连接到节点 的边集, 为节点 的邻居。

上图中, 表示 的输入特征, 包含了边 和 , 包含了节点 和 。
令 和 分别表示状态、输出、特征和所有节点特征的向量,有:
其中, 为 global transition function, 为 global output function,分别为图中所有节点的 local transition function 和 local output function 的堆叠版本。依据 Banach 的 Fixed Point Theorem,GNN 利用传统的迭代方式计算状态:
其中, 表示第 论循环 的值。
介绍完 GNN 的框架后,下一个问题就是如果学习得到 local transition function 和 local output function 。在包含目标信息( 对于特定节点)的监督学习情况下,损失为:
其中, 为用于监督学习的节点数量。利用基于梯度下降的学习方法优化模型后,我们可以得到针对特定任务的训练模型和图中节点的隐含状态。
尽管实验结果表明 GNN 是一个用于建模结构数据的强大模型,但对于一般的 GNN 模型仍存在如下缺陷:
对于固定点,隐含状态的更新是低效地。 GNN 在每一轮计算中共享参数,而常见的神经网络结构在不同层使用不同的参数。同时,隐含节点状态的更新可以进一步应用 RNN 的思想。 边上的一些信息特征并没有被有效的建模,同时如何学习边的隐含状态也是一个重要问题。 如果我们更关注节点的表示而非图的表示,当迭代轮数 很大时使用固定点是不合适的。这是因为固定点表示的分布在数值上会更加平滑,从而缺少用于区分不同节点的信息。
Graph Convolutional Networks
图卷积神经网络是将用于传统数据(例如:图像)的卷积操作应用到图结构的数据中。核心思想在于学习一个函数 ,通过聚合节点 自身的特征 和邻居的特征 获得节点的表示,其中 为节点的邻居。
下图展示了一个用于节点表示学习的 GCN 过程:

GCN 在构建更复杂的图神经网路中扮演了一个核心角色:

包含 Pooling 模块用于图分类的 GCN
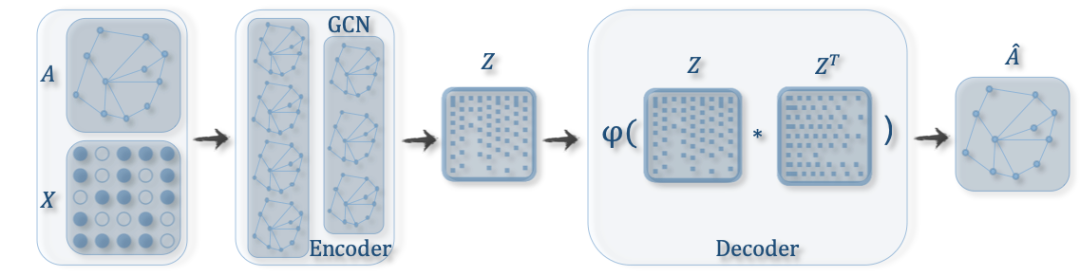
包含 GCN 的图自编码器

包含 GCN 的图时空网络
GCN 方法可以分为两大类:基于频谱(Spectral Methods)和基于空间(Spatial Methods)的方法。
基于频谱的方法(Spectral Methods)
基于频谱的方法将图视为无向图进行处理,图的一种鲁棒的数学表示为标准化的图拉普拉斯矩阵:
其中, 为图的邻接矩阵, 为节点度的对角矩阵,。标准化的拉普拉斯矩阵具有实对称半正定的性质,因此可以分解为:
其中, 是由 的特征向量构成的矩阵, 为特征值的对角矩阵,。在图信号处理过程中,一个图信号 是一个由图的节点构成的特征向量,其中 表示第 个节点的值。对于信号 ,图上的傅里叶变换可以定义为:
傅里叶反变换定义为:
其中, 为傅里叶变换后的结果。
转变后信号 的元素为新空间图信号的坐标,因此输入信号可以表示为:
这正是傅里叶反变换的结果。那么对于输入信号 的图卷积可以定义为:
其中, 为滤波器, 表示逐元素乘。假设定义一个滤波器 ,则图卷积可以简写为:
基于频谱的图卷积网络都遵循这样的定义,不同之处在于不同滤波器的选择。
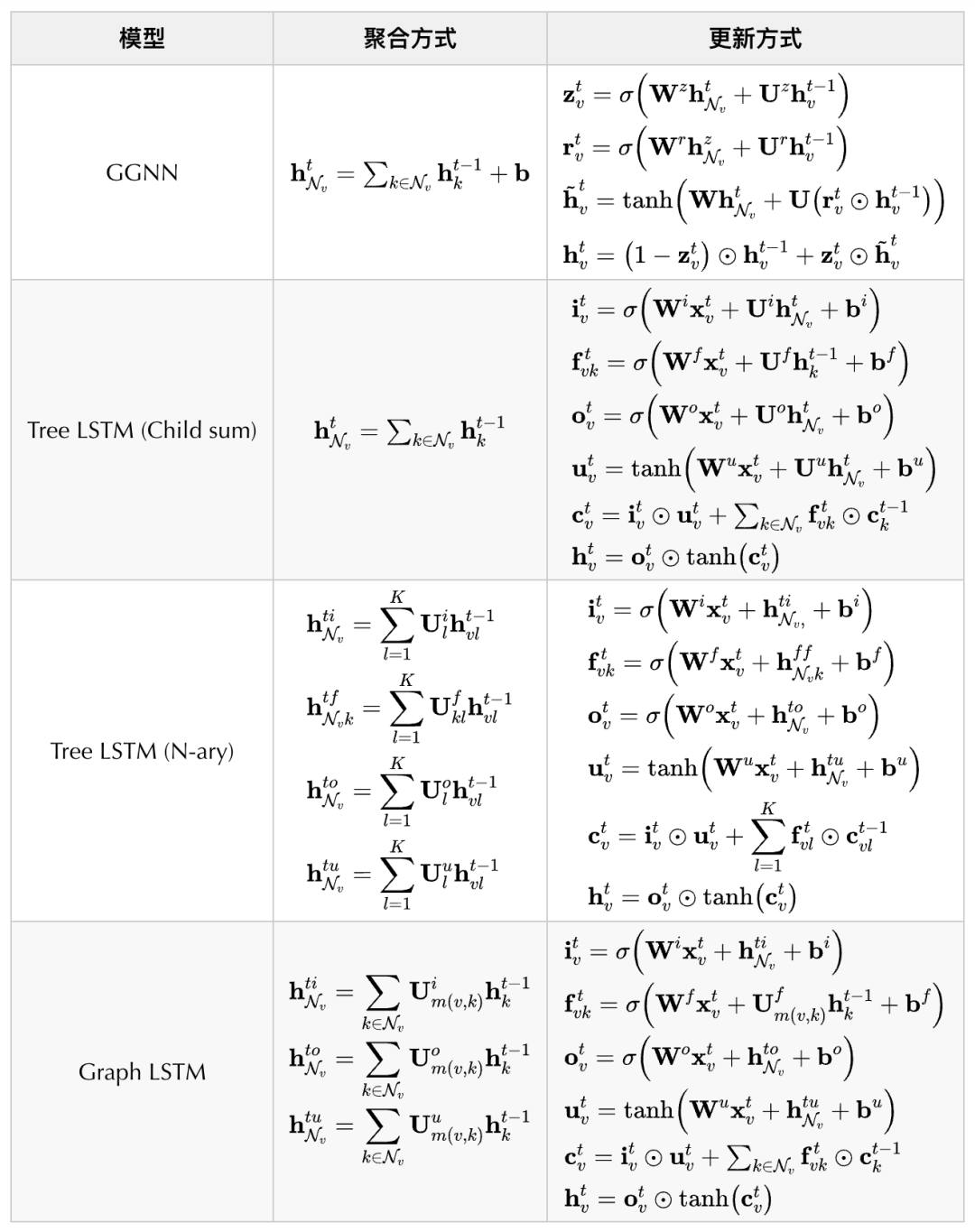
一些代表模型及其聚合和更新方式如下表所示:

基于空间的方法(Spatial Methods)
基于空间的方法通过节点的空间关系来定义图卷积操作。为了将图像和图关联起来,可以将图像视为一个特殊形式的图,每个像素点表示一个节点,如下图所示:

每个像素同周围的像素相连,以 为窗口,每个节点被 8 个邻居节点所包围。通过对中心节点和周围邻居节点的像素值进行加权平均来应用一个 大小的滤波器。由于邻居节点的特定顺序,可以在不同位置共享权重。同样对于一般的图,基于空间的图卷积通过对中心和邻居节点的聚合得到节点新的表示。
为了使节点可以感知更深和更广的范围,通常的做法是将多个图卷积层堆叠在一起。根据堆叠方式的不同,基于空间的图卷积可以进一步分为两类:基于循环(Recurrent-based)和基于组合(Composition-based)的。基于循环的方法使用相同的图卷积层来更新隐含表示,基于组合的方式使用不同的图卷积层更新隐含表示,两者差异如下图所示:

一些代表模型及其聚合和更新方式如下表所示:

Graph Recurrent Networks
一些研究尝试利用门控机制(例如:GRU 或 LSTM)用于减少之前 GNN 模型在传播过程中的限制,同时改善在图结构中信息的长距离传播。GGNN 提出了一种使用 GRU 进行传播的方法。它将 RNN 展开至一个固定 步,然后通过基于时间的传导计算梯度。传播模型的基础循环方式如下:
节点 首先从邻居汇总信息,其中 为图邻接矩阵 的子矩阵表示节点 及其邻居的连接。类似 GRU 的更新函数,通过结合其他节点和上一时间的信息更新节点的隐状态。 用于获取节点 邻居的信息, 和 分别为更新和重置门。
GGNN 模型设计用于解决序列生成问题,而之前的模型主要关注单个输出,例如:节点级别或图级别的分类问题。研究进一步提出了 Gated Graph Sequence Neural Networks(GGS-NNs),使用多个 GGNN 产生一个输出序列 ,如下图所示:

上图中使用了两个 GGNN, 用于从 预测 , 用于从 预测 。令 表示第 步输出的第 步传播, 在任意 步初始化为 , 在任意 步初始化为 , 和 可以为不同模型也可以共享权重。
一些代表模型及其聚合和更新方式如下表所示:
Graph Attention Networks
与 GCN 对于节点所有的邻居平等对待相比,注意力机制可以为每个邻居分配不同的注意力评分,从而识别更重要的邻居。
GAT 将注意力机制引入传播过程,其遵循自注意力机制,通过对每个节点邻居的不同关注更新隐含状态。GAT 定义了一个图注意力层(graph attentional layer),通过堆叠构建图注意力网络。对于节点对 ,基于注意力机制的系数计算方式如下:
其中, 表示节点 对 的注意力系数, 表示节点 的邻居。令 表示输入节点特征,其中 为节点的数量, 为特征维度,则节点的输出特征(可能为不同维度 )为 。 为所有节点共享的线性变换的权重矩阵, 用于计算注意力系数。最后的输出特征计算方式如下:
注意力层采用多头注意力机制来稳定学习过程,之后应用 个独立的注意力机制计算隐含状态,最后通过拼接或平均得到输出表示:
其中, 表示连接操作, 表示第 个注意力机制计算得到的标准化的注意力系数。整个模型如下图所示:

GAT 中的注意力架构有如下几个特点:
针对节点对的计算是并行的,因此计算过程是高效的。 可以处理不同度的节点并对邻居分配对应的权重。 可以容易地应用到归纳学习问题中去。
应用
图神经网络已经被应用在监督、半监督、无监督和强化学习等多个领域。下图列举了 GNN 在不同领域内相关问题中的应用,具体模型论文请参考 Graph Neural Networks: A Review of Methods and Applications。

往期精彩回顾
本站qq群851320808,加入微信群请扫码:
