鸟群的启发--粒子群算法-技术圈

看文章之前先看一个相关小视频（55s, 2.86M）：

1. PSO的基本思想：

“自然界的蚁群、鸟群、鱼群、羊群、牛群、蜂群等，其实时时刻刻都在给予我们以某种启示，只不过我们常常忽略了大自然对我们的最大恩赐！”——马良教授

粒子群算法的思想源于对鸟群捕食行为的研究．模拟鸟集群飞行觅食的行为，鸟之间通过集体的协作使群体达到最优目的。

设想这样一个场景：一群鸟在随机搜索食物

已知：

(1). 在这块区域里只有一块食物;

(2). 所有的鸟都不知道食物在哪里;

(3). 但它们能感受到当前的位置离食物还有多远.

那么:找到食物的最优策略是什么呢？

(1). 搜寻目前离食物最近的鸟的周围区域．

(2). 根据自己飞行的经验判断食物的所在。

PSO正是从这种模型中得到了启发：信息的社会共享

2. 算法介绍

(1)每个寻优的问题解都被想像成一只鸟，称为“粒子”。所有粒子都在一个D维空间进行搜索。

(2)所有的粒子都由一个fitness function 确定适应值以判断目前的位置好坏。

(3)每一个粒子必须赋予记忆功能，能记住所搜寻到的最佳位置。

(4)每一个粒子还有一个速度以决定飞行的距离和方向。这个速度根据它本身的飞行经验以及同伴的飞行经验进行动态调整。

粒子群优化算法求最优解在D维空间中，有N个粒子；

粒子i位置：x_i=(x_i1,x_i2,…x_iD)，将xi代入适应函数f(x_i)求适应值；

粒子i速度：v_i=(v_i1,v_i2,…v_iD)

粒子i个体经历过的最好位置：pbest_i=(p_i1,p_i2,…p_iD)

种群所经历过的最好位置：gbest=(g1,g2,…gD)

通常，最优粒子第d（1≤d≤D）维的位置变化范围限定在[X_min,d, X_max,d] 内，每个粒子的速度变化范围限定在[-V_min,d, V_max,d]内（即在迭代中若相应粒子速度位置超出了边界值，则该维的速度或位置被限制为该维最大速度或边界位置）

粒子速度更新公式包含三部分：

第一部分为粒子先前的速度

第二部分为“认知”部分，表示粒子本身的思考，可理解为粒子i当前位置与自己最好位置之间的距离。

第三部分为“社会”部分，表示粒子间的信息共享与合作，可理解为粒子i当前位置与群体最好位置之间的距离。

3. 算法流程图

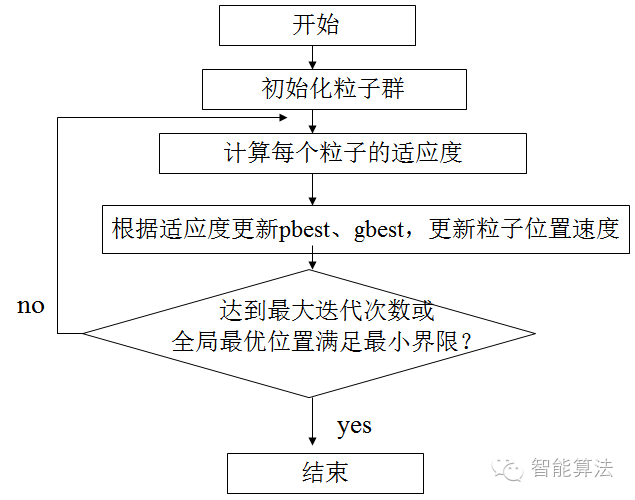
(1)Initial：

初始化粒子群体（群体规模为n），包括随机位置和速度。

(2)Evaluation：

根据fitness function ，评价每个粒子的适应度。

(3)Find the Pbest：

对每个粒子，将其当前适应值与其个体历史最佳位置（pbest）对应的适应值做比较，如果当前的适应值更高，则将用当前位置更新历史最佳位置pbest。

(4)Find the Gbest：

对每个粒子，将其当前适应值与全局最佳位置（gbest）对应的适应值做比较，如果当前的适应值更高，则将用当前粒子的位置更新全局最佳位置gbest。

(5)Update the Velocity：

根据公式更新每个粒子的速度与位置。

(6)如未满足结束条件，则返回步骤2

通常算法达到最大迭代次数G_max或者最佳适应度值的增量小于某个给定的阈值时算法停止。

4. 算法举例

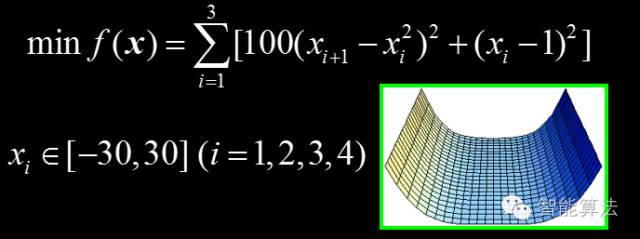
求解如下四维Rosenbrock函数的优化问题

种群的数量：m=5，

编码：因为问题的维数是4，所以粒子的位置和速度都是四维实数向量

设定粒子的速度范围（一般为位置的范围）：V_max=60

对粒子群进行位置和速度的随机初始化，如下：

至此，每个粒子的初始位置和初始速度都已确定，接下来根据目标函数f(x)计算每个粒子的适应值：

从适应值上我们可以得出群体历史最优解x_1,和个体历史最优解，每个解本身。接下来更新粒子位置和速度：设w=1,c_1=c_2=2，根据上面的速度位置更新函数，根据规则，每个粒子的速度和最优粒子位置超过限制将强行拉回边界，可以得到更新后的速度和位置如下：

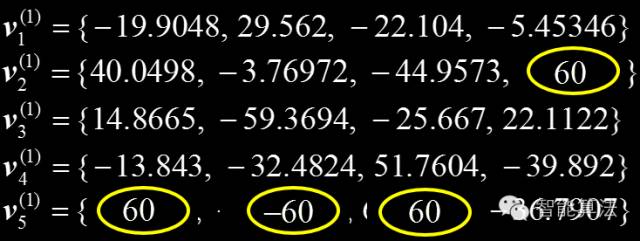
然后，根据新位置继续计算适应值，根据适应值替换全局历史最优粒子和个体历史最优粒子。直至达到最大迭代次数G_max或者最佳适应度值的增量小于某个给定的阈值时算法停止。

5. 小结

PSO从这种模型中得到启示并用于解决优化问题。PSO中，每个优化问题的解都是搜索空间中的一只鸟。我们称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值(fitnessvalue)，每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。

免责声明：本文系网络转载。版权归原作者所有。如涉及版权，请联系删除！