1值域空间

矩阵 的值域为: 由 的值域生成的 的子空间，记为 。即，

因为 是向量 经矩阵 变换后的所有像（image）的集合，所以也可以将 称为 的像空间。

同样， 的值域是 的子空间，记为 。即，

.列空间

矩阵向量乘积 可以看成关于矩阵 的列向量集合的一个线性组合，这是为值域空间提供了另一种解释。

我们这么来看，当允许向量

的分量自由变化的话，有

可以看出， 的所有像的集合与 的列的所有线性组合的集合是相同的。

因此， 就是矩阵 的列所张成的空间。这就是为什么 通常也被称为 的列空间的原因。

.行空间

同样， 是 的列所张成的空间。而 的列同时也是 的行，换句话说， 可以看成是矩阵 的行张成的空间。因此， 也被称为 的行空间。

.几个概念的关系

• 矩阵 的值域（range）空间、像（image）空间和列（column）空间是指同一个东西。

• 的列空间等于 的行空间，而 的行空间等于 的列空间。

对于矩阵 ，有

• 由 的列张成的空间（列空间）。

• 由 的行张成的空间（行空间）。

• 。

• 。

2零空间

下面看一下零空间和左零空间的定义，

• 对于 矩阵 ，集合

称为矩阵 的零空间。换句话说， 是齐次系统 所有解的集合。

• 集合

称为 的左零空间，因为 是左侧齐次系统 所有解的集合。

注意，零空间（nullspace）也有别的叫法，那就是核（kernel）。

那么，给你一个矩阵，怎么求它对应的这些子空间呢？可以用高斯消元，但是如果先对这个矩阵作奇异值分解，我们也可以很轻松获得副产品，那就是这些子空间。

3SVD 与子空间

是一个秩为 的 矩阵，其 SVD 分解为 ，其中

和

把矩阵 和 按列分成两部分，并令

以及

则可以得到矩阵 对应的四个基本子空间，

1、左奇异向量集 是矩阵 的列空间的标准正交基，即

2、左奇异向量集 是 的零空间的标准正交基，即

3、右奇异向量集 是矩阵 的行空间的标准正交基，即

4、右奇异向量集 是 的零空间的标准正交基，即

.验证

下面我们对矩阵的 的值域空间（列空间）和零空间作个简单验证，矩阵 对应的子空间也类似。

 1、假设 的秩为 ，因此奇异值为

因为 ，代入 有，

因此可得，矩阵 的值域空间，

2、观察下式何时为 ？

令 ，代入 得，

可知，矩阵 的零空间为，

.分开看和

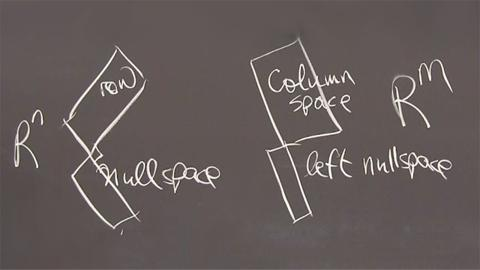
上图的左半部分，从矩阵 的列来看，可以分成两部分，

上图的右半部分，从矩阵 的列来看，可以分成两部分，

.图表结合速记

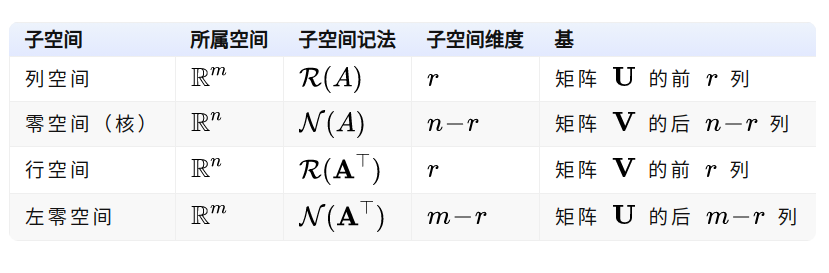
最后，回到开头那张图，总结一下矩阵 的 SVD 分解与四个基本子空间之间的联系。需要注意的是，下图中的空间的简写跟上文中的标记有点点区别，它这里的 、 和 分别指列空间、行空间和零空间。

为方便记忆，我们把四个子空间及基本性质放在一个表格中。

矩阵 的秩为 ，则有如下四个基本子空间:

.一图速记

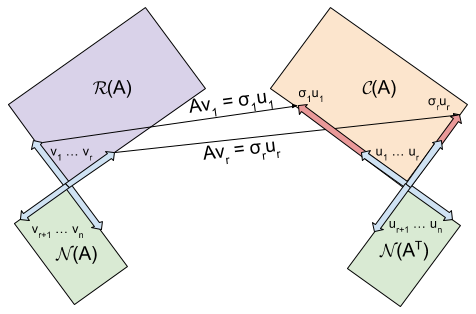
下面这张图将上面两张图合二为一，使得 SVD 与四个子空间的关系展示得更加精炼、清晰。

4有啥应用？

这几个子空间咋一看貌似有点乱，但仔细一看还是井井有条的样子嘛。稍微理一理，还是好理解的。

有些朋友或许会问，除了理论价值，这有什么具体应用吗？有的，其实还挺多的，有些应该算是大家很熟悉的应用。