三边测距定位算法详解
来源:平行机器人 | 赵得江
整理:李肖遥
通过GPS定位系统实现无人机的空中悬停定点飞行
“定位”这个概念我想大家并不陌生,可以说定位技术的迅猛发展给我们的日常生活带来了极大的便利。比如,手机的定位导航系统让“路痴”再也不怕出远门了;航天飞行器可以自由地穿梭于浩瀚的宇宙却逃不出人类的掌控;无人驾驶技术更是离不开定位系统的支撑……

接下来将向大家介绍一种简单的定位算法——三边测距定位算法。
【简介】
简单的说,实现定位你只需要做好以下两点:
测量值 从某种意义上说,几乎所有你能测量的数据都取决于“位置”,并且可以利用测得的数据进行定位。最理想的情况是测量那些对“位置”非常敏感的数据。例如,测量温度可能会知道你身在哪个大陆,当然这样的结果并不准确,但是如果测量的是你相对于某些点的距离或者角度,那么对你的位置的定位可能会更精确一些。
参考点 描述一个确定的位置,正确的方法就是描述它相对于某些参考点的位置。参考点可以是“你的家”、“北极星”或“天空中的一些卫星”。对我们来说,我们将使用锚。利用3个锚点就可以描述一个二维的坐标系统,在这个系统中我们可以找到我们的位置。对于三维定位系统,我们则需要4个锚点。
下面是一些例子:
定位系统 | 测量值 | 参考点 |
GPS | 距离* | 卫星 |
Pozyx | 距离 | 锚 |
摄像机 | 视频图像 | 相机指定方向 |
WiFi、指纹识别 | 接收信号强度 | 数据库中的指纹 |
数字罗盘 | 磁场矢量 | 磁场北极 |
航位推算 | 加速度和角速度(来自陀螺仪) | 最初的位置和方向 |
注意:一些GPS接收器也使用多普勒频移定位
【三边测距法】
最常用的定位方法是使用基本的几何图形来估计位置。通过测量与锚点的距离,就可以确定你的位置。如果我们只知道自己与锚点的距离,那么我们的位置肯定会在以锚点P为圆心以测得距离d为半径的圆上。如果我们用3个锚进行距离测量,我们会发现我们的位置在三个圆的交点上,如图1所示。这种方法被称为三边测距法(如果使用的锚点数量超过3个,则称为多边测距法)。
这种方法的困难在于测量中总会有一些噪音,测量并不完美。因此,圆不会在一个点相交。为了解决这个问题,我们试着找出最接近所有圆的点。
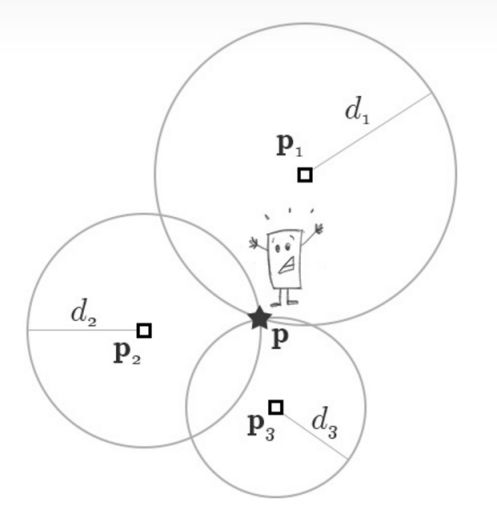
图1 三边测量

注:你可以选择跳过该算法的描述,直接参阅下一篇文章:超宽带是如何工作的。
【一个基本的算法】
在本节中,我们将介绍一种简单的算法,它可以从一系列的范围测量中计算出位置。这个基本算法不是最优的,但是当范围测量足够精确时,它就会很好地工作。
我们将解释2D定位的算法。位置P由坐标x和y给出。第i个锚点pi的位置坐标为(xi,yi),如果我们有N个锚,那么i的取值为从1到N,这些锚点的坐标是已知的。
现在,位置P与第i个锚点之间的距离由di表示,di由下面的公式给出:
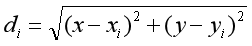
对等式两边取平方:
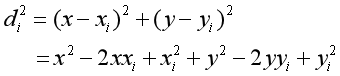
上面方程的问题在于含有非线性项x^2和y^2。我们可以通过从di^2中减去dN^2来消除这些非线性项,得到N-1个方程,其中第i个方程式为:
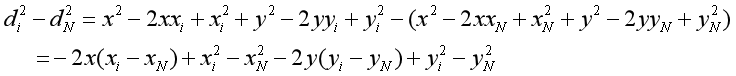
现在我们有了一些关于坐标x和y的线性方程,这很好,因为线性方程很容易求解。我们把它写成矩阵的形式:
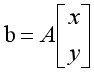
其中
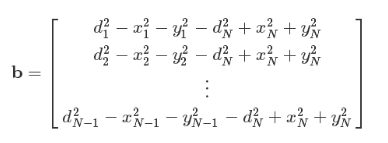
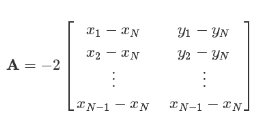
我们现在可以解这个方程组了。
如果我们恰好有3个锚点:N=3,我们就会得到两个方程来求解两个未知数,通过求解下面的方程,我们可以找到P的位置:
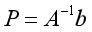
如果我们有超过3个锚点:N>3,我们得到的方程的数量要多于未知数的数量,此时A的逆矩阵是不存在的。为了解决这个问题,我们可以利用伪逆算子来计算这个位置。这就产生了下面的方程式:
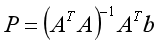
请注意,上面的公式将尽可能地将坐标x和y与所有不同的方程相匹配。因此,当使用更多的锚时,定位的准确性也会随之提高。
上面描述的算法被称为线性最小二乘算法。“线性”是因为我们把方程进行了线性化(通过平方)和“最小二乘”是因为矩阵的(伪)逆矩阵会使所有方程的平方误差最小化。
【拓展】
上面描述的算法是一种非常简单和低复杂度的算法。如果你想了解更多关于先进定位技术的知识,建议你寻找以下主题:非线性最小二乘、卡尔曼滤波、粒子滤波、置信传播……
来源整理于网络素材,版权归原作者所有,如有侵权,请联系删除,谢谢。
‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧ END ‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧ 关注我的微信公众号,回复“加群”按规则加入技术交流群。
点击“阅读原文”查看更多分享,欢迎点分享、收藏、点赞、在看。
