人理解算法,神定义哲学
点击蓝字
关注我们
#85#
 ————————
———————— 递归、分治、动态规划、贪心、回溯、分支限界这些算法,原本都是为了解决问题。
但了解算法,会发现古老的哲学。
无论是否跟产品经理岗位,甚至IT行业打交道,都会被算法背后的智慧吸引。
1
递归算法
(recursion algorithm)
大师 L. Peter Deutsch 说过:To Iterate is Human, to Recurse, Divine。译为:
人理解迭代,神理解递归。
在算法领域,直接或间接地调用自身的算法,就称为递归算法。
典型代表:Fibonacci函数、Hanoi问题、数据结构(二叉树、广义表)
案例:Fibonacci函数
即斐波那契数列,又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”。
我们都知道黄金分割,但是实际上和自然界的繁殖生息如此紧密。

一对兔子,每个月能生出一对小兔子来。如果所有兔子都不死,那么一年以后可以繁殖多少对兔子?
第一个月小兔子没有繁殖能力,所以还是一对;两个月后,生下一对小兔对数共有两对;三个月以后,老兔子又生下一对,因为小兔子还没有繁殖能力,所以一共是三对……
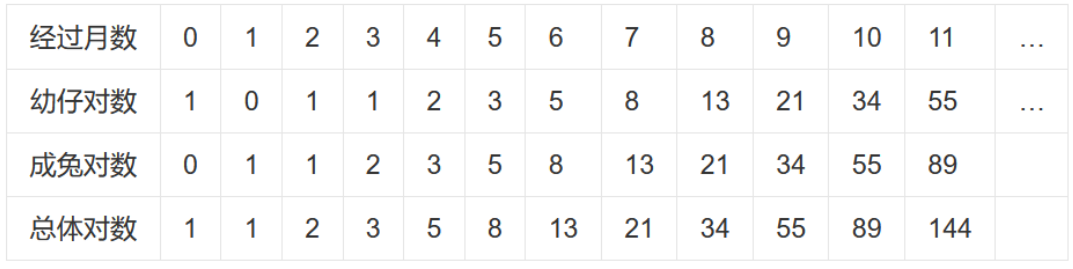
这个规律,就是生物学上著名的“鲁德维格定律”。
此外,观察延龄草、野玫瑰、南美血根草、大波斯菊、金凤花、耧斗菜、百合花、蝴蝶花的花瓣,可以发现它们花瓣数目具有斐波那契数:3、5、8、13、21……
2
分治法
(divide and conquer method)
将待求解的原问题划分成k个较小规模的子问题,对这k个子问题分别求解。
如果子问题的规模仍然不够小,则再将每个子问题划分为k个规模更小的子问题,如此分解下去,直到问题规模足够小.
再将子问题的解合并为一个更大规模的问题的解,自底向上逐步求出原问题的解。
典型代表:二分搜索、棋盘覆盖、合并排序、最接近点对问题、循环赛日程表、汉诺塔、Fibonacci数列、阶乘、快速排序......
案例:汉诺塔(Tower of Hanoi)
又称河内塔,是一个源于印度古老传说的益智玩具。

大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。
大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
有预言说,这件事完成时宇宙会在一瞬间闪电式毁灭。也有人相信婆罗门至今还在一刻不停地搬动着圆盘。
上升到文化、宇宙、时间的话题,总是那么引人入胜!
如果移动一个圆盘需要1秒钟的话,等到64个圆盘全部重新落在一起,宇宙被毁灭是什么时候呢?
3
动态规划法
(dynamic programing method)
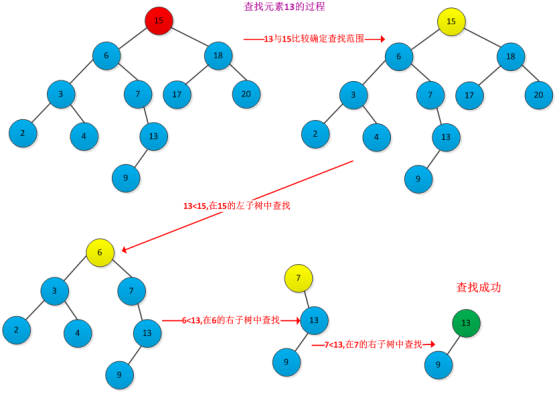
将待求解问题分解成若干个相互重叠的子问题,每个子问题对应决策过程的一个阶段。
一般来说,子问题的重叠关系表现在对给定问题求解的递推关系(也就是动态规划函数)中,将子问题的解求解一次并填入表中,当需要再次求解此子问题时,可以通过查表获得该子问题的解而不用再次求解,从而避免了大量重复计算。
典型代表:最长公共子序列、最优二叉查找树、近似串匹配问题......
4
贪心法
(greedy method)
贪心法在解决问题的策略上目光短浅,只根据当前已有的信息就做出选择,而且一旦做出了选择,不管将来有什么结果,这个选择都不会改变。
换言之,贪心法并不是从整体最优考虑,它所做出的选择只是在某种意义上的局部最优。
这种局部最优选择并不总能获得整体最优解(Optimal Solution),但通常能获得近似最优解(Near-Optimal Solution)。
典型代表:TSP问题(最近邻点)、TSP问题(最短链接)、图着色、背包问题、多极度调度问题、霍夫曼编码、单源最短路径(Dijkstra算法)、最小生成树(Prim和Kruskal算法)
案例:背包问题(Knapsack problem)
可追溯到1897年数学家托比亚斯·丹齐格(Tobias Dantzig,1884-1956),指的是包装你最有价值或有用的物品,而不会超载你的行李的常见问题。
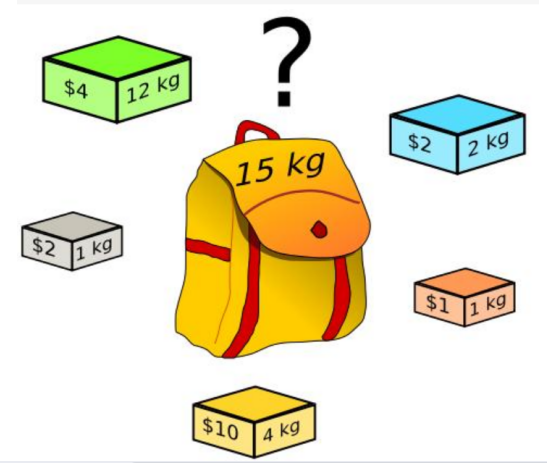
问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。
如何选择最合适的物品放置于给定背包中。相似问题经常出现在商业、组合数学,计算复杂性理论、密码学和应用数学等领域中。
5
回溯法
(back track method)
回溯法就是一种有组织的系统化搜索技术,可以看作是蛮力法穷举搜索的改进。
回溯法每次只构建可能解的一部分,然后评估这个部分解,如果这个部分有可能导致一个完全解,对其进一步搜索,否则,就不必继续构造这部分的解了,回溯法常常可以避免搜索所有可能的解.
所以,它往往比满立法效率更高,适用于求解组合数组较大的问题。
回溯法是以深度优先方式搜索问题解的算法,它适用于组合数较大的问题,能系统地搜索到一个问题的所有解惑任一解。
典型代表:哈密顿回路问题、八皇后问题、批处理作业调度......
案例:八皇后问题(Eight queens)
八皇后问题是国际象棋棋手马克斯·贝瑟尔于1848年提出的问题,是回溯算法的典型案例。

问题表述为:在8×8格的国际象棋上摆放8个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解,后来有人用图论的方法解出92种结果。计算机发明后,有多种计算机语言可以编程解决此问题。
6分支限界法(branch and bound method)
分支限界法按广度优先策略遍历问题的解空间,在遍历过程种,对已经处理的每一个结点根据限界函数估算目标函数的可能值,从中选取使目标函数取得极值(极大或极小)的结点优先进行广度优先搜索,从而不断调整搜索方向,尽快找到问题的解。
因为界限函数常常是基于问题的目标函数而确定的,所以,分支限界法适用于求解最优化问题。
分支界限法的求解目标是找出满足约束条件的一个解,或是在满足约束条件的解中找出使某一目标函数值达到极大或极小的解,即在某种意义下的最优解。(分支界限法与回溯法求解目标不同).
典型代表:任务分配问题、多段图的最短路径问题、批处理作业调度问题、电路布线问题......
案例:任务分配问题


问题描述:N个人分配N项任务,一个人只能分配一项任务,一项任务只能分配给一个人,将一项任务分配给一个人是需要支付报酬,如何分配任务,保证支付的报酬总数最小。
总结:
产品、代码、算法等,在文化面前是短浅的。
只有探索、思考,超出人类所知的,并在历史中沉淀下来的难题,才可以直指宇宙、时空、哲学域。
感受到这种永恒的魅力了嘛!
END
赠送一些我喜欢的电子书

获取方式:第一步:请分享本文到朋友圈,点赞和在看
第二步:在公众号"唧唧歪歪PM"回复:1
