​【机器学习】数据科学中 17 种相似性和相异性度量(下)

⑦ 皮尔逊相关距离

相关距离量化了两个属性之间线性、单调关系的强度。此外，它使用协方差值作为初始计算步骤。但是，协方差本身很难解释，并且不会显示数据与表示测量之间趋势的线的接近或远离程度。

为了说明相关性意味着什么，回到我们的 Iris 数据集并绘制 Iris-Setosa 样本以显示两个特征之间的关系：花瓣长度和花瓣宽度。

已估计相同花卉样本的两个特征的样本均值和方差，如下图所示。

一般来说，我们可以说花瓣长度值相对较低的花的花瓣宽度值也相对较低。此外，花瓣长度值相对较高的花朵也具有花瓣宽度值相对较高的值。此外，我们可以用一条线来总结这种关系。

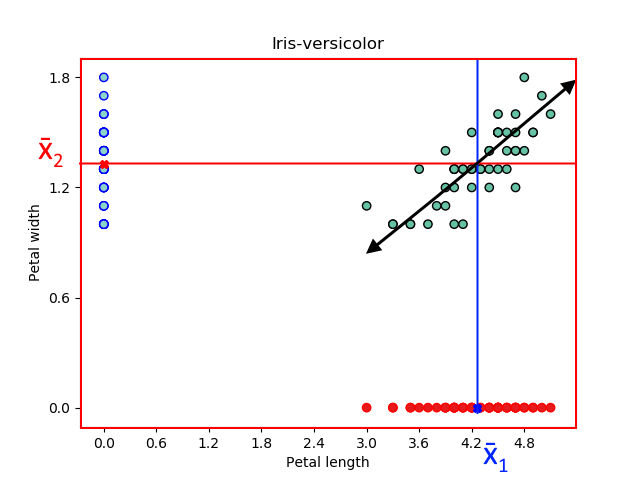
这条线表示花瓣长度和花瓣宽度的值一起增加的积极趋势。

协方差值可以对三种关系进行分类：

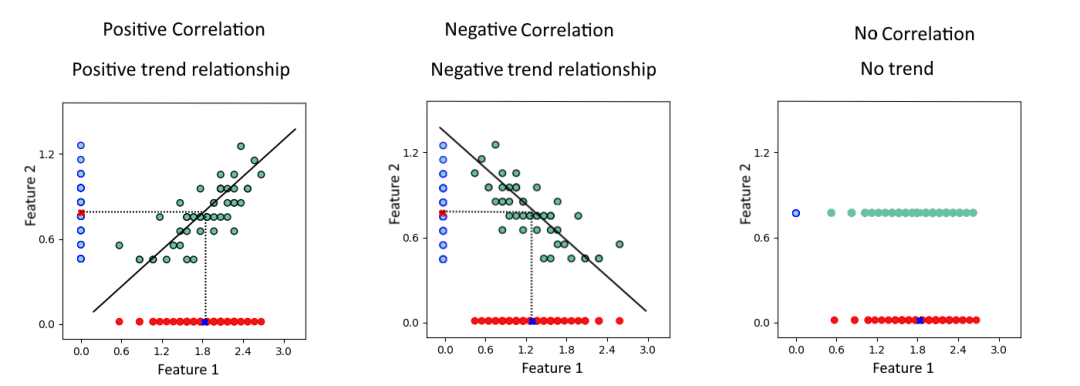
相关距离可以使用以下公式计算：

其中分子表示观测值的协方差值，分母表示每个特征方差的平方根。

举一个简单的例子来演示我们如何计算这个公式。

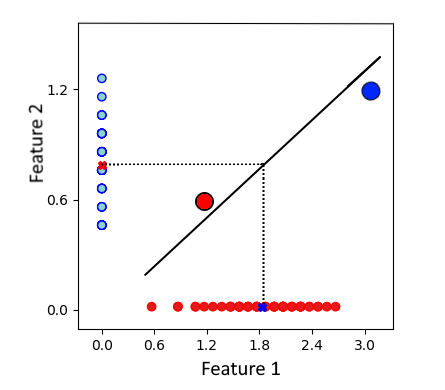
红点和蓝点分别具有以下坐标：

A(1.2, 0.6) 和 B (3.0, 1.2)。

两次测量的估计样本均值等于：

该指标的最后一点是相关性并不意味着因果关系。例如，具有相对较小花瓣长度值的iris-Setosa 并不意味着花瓣宽度值也应该较小。是充分条件但不是必要条件！可以说，小花瓣长度可能导致小花瓣宽度，但不是唯一的原因！

⑧ 斯皮尔曼相关

与 Pearson 相关性一样，每当我们处理双变量分析时，都会使用 Spearman 相关性。但是，与 Pearson 相关性不同，Spearman 相关性在两个变量都按等级排序时使用，它可用于分类和数字属性。

斯皮尔曼相关指数可以使用以下公式计算：

Spearman 相关性常用于假设检验。

⑨ 马氏距离

马氏距离Mahalanobis是一种主要用于多变量统计测试的度量指标，其中欧氏距离无法给出观测值之间的实际距离。它测量数据点离分布有多远。

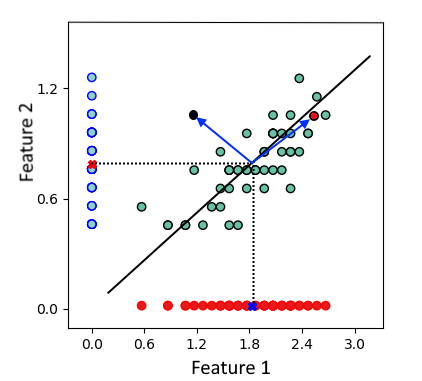
来自平均值的具有相同 ED 值的两个点。

如上图所示，红点和蓝点与均值的欧几里得距离相同。但是，它们不属于同一区域或集群：红点更有可能与数据集相似。但是蓝色的被认为是异常值，因为它远离代表数据集中最大可变性方向的线（长轴回归）。因此，引入了马哈拉诺比斯度量来解决这个问题。

Mahalanobis 度量试图降低两个特征或属性之间的协方差，因为您可以将之前的图重新缩放到新轴。并且这些新轴代表特征向量，如前面所示的第一个特征向量。

特征向量的第一个方向极大地影响了数据分类，因为它具有最大的特征值。此外，与其他垂直方向相比，数据集沿该方向展开得更多。

使用这种技术，我们可以沿着这个方向缩小数据集并围绕均值（PCA）旋转它。然后我们可以使用欧几里得距离，它给出了与前两个数据点之间的平均值的不同距离。这就是马哈拉诺比斯指标的作用。

两个物体 P 和 Q 之间的马氏距离。

其中C表示属性或特征之间的协方差矩阵。

为了演示这个公式的用法，我们计算 A(1.2, 0.6) 和 B (3.0, 1.2) 之间的距离，来自之前在相关距离部分的例子。

现在评估协方差矩阵，其定义二维空间中的协方差矩阵如下：

其中 Cov[P,P] = Var[P] 和 Cov[Q,Q]= Var[Q]，以及两个特征之间的协方差公式：

因此，两个物体 A 和 B 之间的马哈拉诺比斯距离可以计算如下：

除了其用例之外，马哈拉诺比斯距离还用于Hotelling t 方检验^[2]。

⑩ 标准化欧几里得距离

标准化或归一化是在构建机器学习模型时在预处理阶段使用的一种技术。该数据集在特征的最小和最大范围之间存在很大差异。在对数据进行聚类时，此比例距离会影响 ML 模型，从而导致错误的解释。

例如，假设有两个不同的特征，它们在范围变化方面表现出很大差异。例如，假设有一个从 0.1 到 2 变化的特征和另一个从 50 到 200 变化的特征。使用这些值计算距离会使第二个特征更具优势，从而导致不正确的结果。换句话说，欧氏距离将受到具有最大值的属性的高度影响。

这就是为什么标准化是必要的，以便这些特征以平等地做出贡献。它是通过将变量转换为所有具有等于 1 的相同方差并将特征集中在平均值周围来完成的，如下面的公式所示 Z 分数标准化：

标准化的欧几里德距离可以表示为：

可以应用这个公式来计算 A 和 B 之间的距离。

⑪ 卡方距离

卡方距离通常用于计算机视觉中，同时进行纹理分析，以发现归一化直方图之间的（不同）相似性，称为“直方图匹配”。

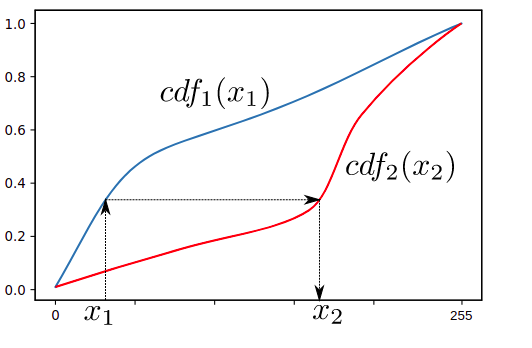
直方图匹配。资料来源：维基百科直方图匹配^[3]

人脸识别算法将是一个很好的例子，它使用这个指标来比较两个直方图。例如，在新面孔的预测步骤中，模型根据新捕获的图像计算直方图，将其与保存的直方图（通常存储在 .yaml 文件中）进行比较，然后尝试为其找到最佳匹配。这种比较是通过计算每对 n 个 bin 的直方图之间的卡方距离来进行的。

此公式与标准正态分布的卡方统计检验不同，后者用于使用以下公式决定是保留还是拒绝原假设：

其中 O 和 E 分别代表观察到的和预期的数据值。

假设对 1000 人进行了一项调查，以测试给定疫苗的副作用，并查看是否存在基于性别的显着差异。因此，每个人都可以是以下四类之一：

1- 男性无副作用。
2- 男性有副作用。
3- 女性无副作用。
4- 有副作用的女性。

零假设是：两种性别之间的副作用没有显着差异。

为了接受或拒绝此假设，可以计算以下数据的卡方检验值：

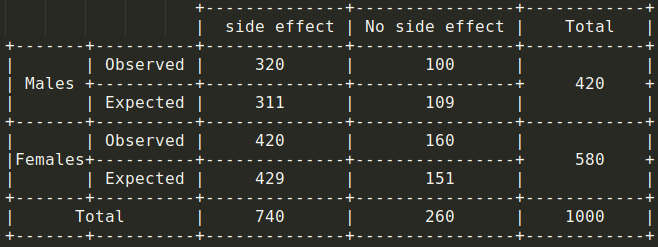
通过将这些值代入卡方检验公式，将得到 1.7288。

使用自由度等于1的卡方表^[4]，将获得介于 0.2 和 0.1 > 0.05 之间的概率 → 接受原假设。

请注意，自由度 =（列数 -1）x（数量或行数 -1）

这里只是想让你快速回顾一下假设检验；我希望你觉得这对你有帮助。

⑫Jensen-Shannon 距离

Jensen-Shannon 距离计算两个概率分布之间的距离。它使用 Kullback Leibler divergence（相对熵）公式来计算距离。

Jensen-Shannon 距离。

其中 R 是 P 和 Q 之间的中点。

此外，只需简要说明如何解释熵的值：

事件A的低熵意味着知道这个事件会发生；换句话说，如果事件 A 会发生，我并不感到惊讶，而且我非常有信心它会发生。高熵的类比相同。

另一方面，Kullback Leibler 散度本身不是距离度量，因为它不是对称的：。

⑬ 莱文斯坦距离

用于测量两个字符串之间相似性的度量。它等于将给定字符串转换为另一个字符串所需的最少操作数。共有三种类型的操作：

1. 代换
2. 插入
3. 删除

对于 Levenshtein 距离，替代成本是两个单位，另外两个操作的替代成本是一个。

例如，取两个字符串 s=“Bitcoin”和 t=“Altcoin”。要从 s 到 t，需要用字母“A”和“l”两次替换字母“B”和“I”。因此，d(t, s) = 2 * 2 = 4。

Levenshtein 距离有很多用例，如垃圾邮件过滤、计算生物学、弹性搜索等等。

⑭ 汉明距离

汉明距离等于两个相同长度的码字不同的位数。在二进制世界中，它等于两个二进制消息之间不同位的数量。

例如，可以使用以下方法计算两条消息之间的汉明距离：

它看起来像分类数据上下文中的曼哈顿距离。

对于长度为 2 位的消息，此公式表示分隔两个给定二进制消息的边数。它最多可以等于二。

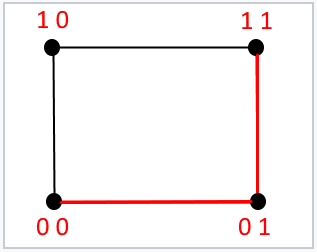
同样，对于长度为 3 位的消息，此公式表示分隔两个给定二进制消息的边数,它最多可以等于三。

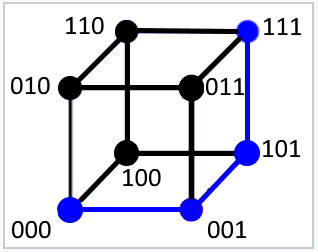
举一些例子来说明汉明距离是如何计算的：

H(100001, 010001) = 2
H(110, 111) = 1

如果其中一个消息包含全零，则汉明距离称为汉明权重，等于给定消息中非零数字的数量。在我们的例子中，它等于 1 的总数。

H(110111,000000) = W (110111) = 5

如果可能，汉明距离用于检测和纠正通过不可靠的噪声信道传输的接收消息中的错误。

⑮ 杰卡德/谷本距离

用于衡量两组数据之间相似性的指标。有人可能会争辩说，为了衡量相似性，需要计算两个给定集合之间的交集的大小（基数、元素数）。

然而，仅凭公共元素的数量并不能告诉我们它与集合大小的相对关系。这就是 Jaccard 系数背后的直觉。

所以Jaccard提出，为了衡量相似度，你需要用交集的大小除以两组数据的并集的大小。

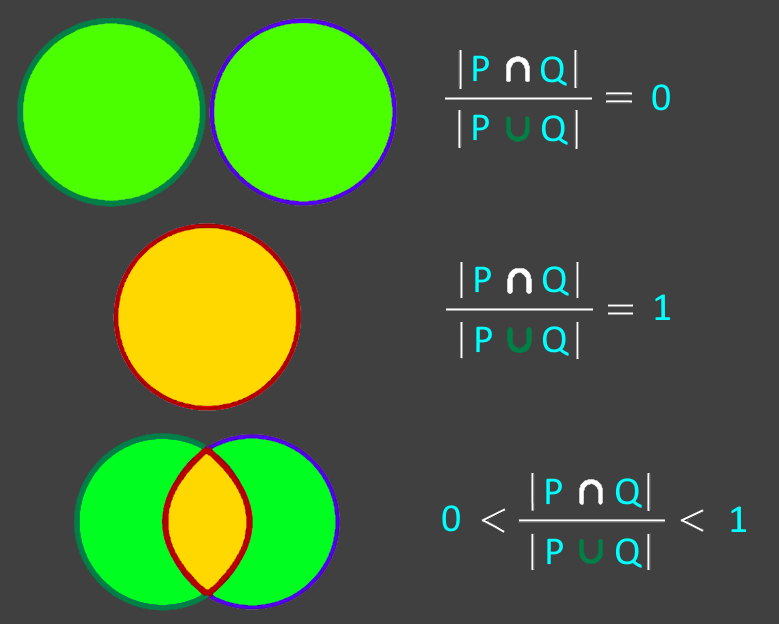
Jaccard 距离与 Jaccard 系数互补，用于衡量数据集之间的差异，计算公式为：

下图说明了如何将此公式用于非二进制数据的Jaccard 索引示例。

对于二元属性，Jaccard 相似度使用以下公式计算：

Jaccard 索引可用于某些领域，如语义分割、文本挖掘、电子商务和推荐系统。

现在你可能会想：“好吧，但你刚才提到余弦距离也可以用于文本挖掘。你更喜欢使用什么作为给定聚类算法的度量？无论如何，这两个指标之间有什么区别？”

很高兴你问了这个问题。为了回答这个问题，我们需要比较两个公式的每一项。
Jaccard 和余弦公式

这两个公式之间的唯一区别是分母项。不是用 Jaccard 计算两个集合之间的联合大小，而是计算 P 和 Q 之间点积的大小。而不是在 Jaccard 公式的分母中添加项；你正在计算余弦公式中两者之间的乘积。我不知道那是什么解释。据我所知，点积告诉我们一个向量在另一个方向上有多少。除此之外，如果有什么要补充的，可在评论区给我留言。

⑯ Sørensen–Dice

Sørensen-Dice 距离是一种统计指标，用于衡量数据集之间的相似性。它被定义为 P 和 Q 的交集大小的两倍，除以每个数据集 P 和 Q 中元素的总和。

Sørensen–Dice 系数。

与 Jaccard 一样，相似度值的范围从零到一。但是，与 Jaccard 不同的是，这种相异性度量不是度量标准，因为它不满足三角不等式条件。

Sørensen–Dice 用于词典编纂^[5]、图像分割^[6]和其他应用程序。

🄲Pydist2

pydist2是一个python包，1:1代码采用pdist^[7]和pdist2^[8] Matlab函数，用于计算观测之间的距离。pydist2 当前支持的测量距离的方法列表可在阅读文档中找到^[9]。

from pydist2.distance import pdist1, pdist2
import numpy as np
x = np.array([[1, 2, 3],
       [7, 8, 9],
       [5, 6, 7],], dtype=np.float32)
y = np.array([[10, 20, 30],
       [70, 80, 90],
       [50, 60, 70]], dtype=np.float32)
a = pdist1(x)
a
>>> array([10.39230485,  6.92820323,  3.46410162])
pdist1(x, 'seuclidean')
>>> array([3.40168018, 2.26778677, 1.13389339])
pdist1(x, 'minkowski', exp=3)
>>> array([8.65349742, 5.76899828, 2.88449914])
pdist1(x, 'minkowski', exp=2)
>>> array([10.39230485,  6.92820323,  3.46410162])
pdist1(x, 'minkowski', exp=1)
>>> array([18., 12.,  6.])
pdist1(x, 'cityblock')
>>> array([18., 12.,  6.])
pdist2(x, y)
>>> array([[ 33.67491648, 135.69819453, 101.26203632],
...       [ 24.37211521, 125.35549449,  90.96153033],
...       [ 27.38612788, 128.80217389,  94.39279634]])
pdist2(x, y, 'manhattan')
>>> array([[ 54., 234., 174.],
...       [ 36., 216., 156.],
...       [ 42., 222., 162.]])
pdist2(x, y, 'sqeuclidean')
>>> array([[ 1134., 18414., 10254.],
...       [  594., 15714.,  8274.],
...       [  750., 16590.,  8910.]])
pdist2(x, y, 'chi-squared')
>>> array([[ 22.09090909, 111.31927838,  81.41482329],
...       [  8.48998061,  88.36363636,  59.6522841 ],
...       [ 11.75121275,  95.51418525,  66.27272727]])
pdist2(x, y, 'cosine')
>>> array([[-5.60424152e-09,  4.05881305e-02,  3.16703408e-02],
...       [ 4.05880431e-02,  7.31070616e-08,  5.62480978e-04],
...       [ 3.16703143e-02,  5.62544701e-04, -1.23279462e-08]])
pdist2(x, y, 'earthmover')
>>> array([[ 90., 450., 330.],
...       [ 54., 414., 294.],
...       [ 66., 426., 306.]])

🄳 写在最后

这里已到达本文的结尾，本次内容已经分享结束了，在本文中，你了解了数据科学中使用的不同类型的指标及其在许多领域的应用。如果你有什么想说的，请尽管在文末留言区留言！

参考资料