​数据科学中 17 种相似性和相异性度量

---

本文解释了计算距离的各种方法，并展示了它们在我们日常生活中的实例。限于篇幅，便于阅读，将本文分为上下两篇，希望对你有所帮助。

"There is no Royal Road to Geometry."—欧几里得

. 简介

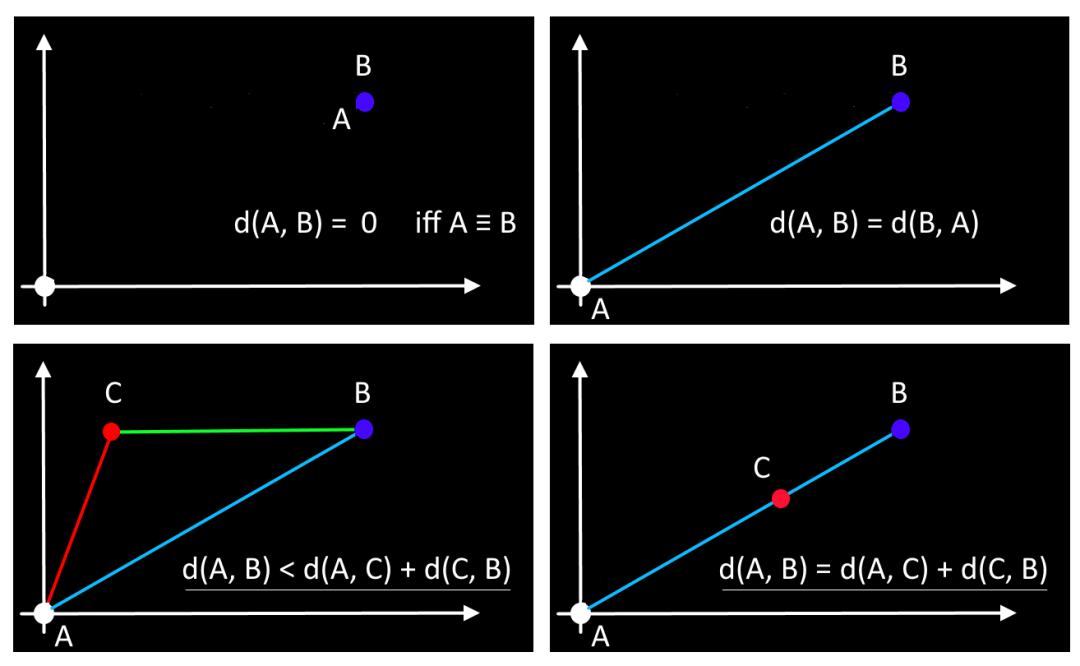
相似性和相异性

在数据科学中，相似性度量是一种度量数据样本之间相互关联或紧密程度的方法。相异性度量是说明数据对象的不同程度。

相异性度量和相似性度量通常用于聚类，相似的数据样本被分组为一个聚类，所有其他数据样本被分组到其他不同的聚类中心中。它们还用于分类（例如 KNN），它是根据特征的相似性标记数据对象。另外还用于寻找与其他数据样本相比不同的异常值（例如异常检测）。

相似性度量通常表示为数值：当数据样本越相似时，它越高。通常通过转换表示为零和一之间的数字：零表示低相似性（数据对象不相似）。一是高相似度（数据对象非常相似）。

举一个例子，有三个数据点 A、B 和 C ，每个数据点只包含一个输入特征。每个数据样本在一个轴上可以有一个值（因为只有一个输入特征），将其表示为 x 轴。并取两个点，A(0.5)、B(1) 和 C(30)，A 和 B 与 C 相比彼此足够接近，因此，A 和 B 之间的相似度高于 A 和 C 或 B 和 C。换句话说，A 和 B 具有很强的相关性。因此，距离越小，相似度就会越大。可以认为这是展示三个数据点 A、B 和 C 之间差异的最简单的例子。

指标

当且仅当满足以下四个条件时，给定的距离（例如相异性）才是度量标准：

1 - 非负性： ，对于任何两个不同的观察  和 。
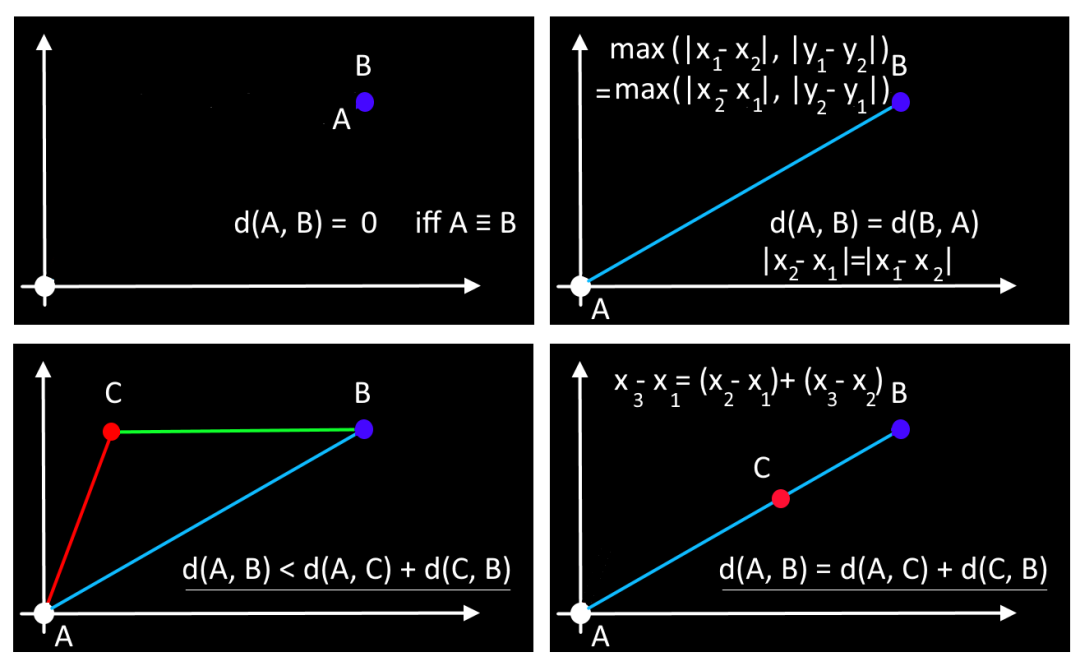
2 - 对称性：  对于所有  和 。
3 - 三角不等式：  对于所有 。
4 -  仅当  时。

距离度量是分类的基本原则，就像 k-近邻分类器算法一样，它测量给定数据样本之间的差异。此外，选择不同的距离度量会对分类器的性能产生很大影响。因此，计算对象之间距离的方式将对分类器算法的性能起到至关重要的作用。

. 距离函数

用于测量距离的技术取决于正在处理的特定情况。例如，在某些区域，欧几里得距离可能是最佳的，并且对于计算距离非常有用。其他应用程序需要更复杂的方法来计算点或观测值之间的距离，如余弦距离。以下列举的列表代表了计算每对数据点之间距离的各种方法。

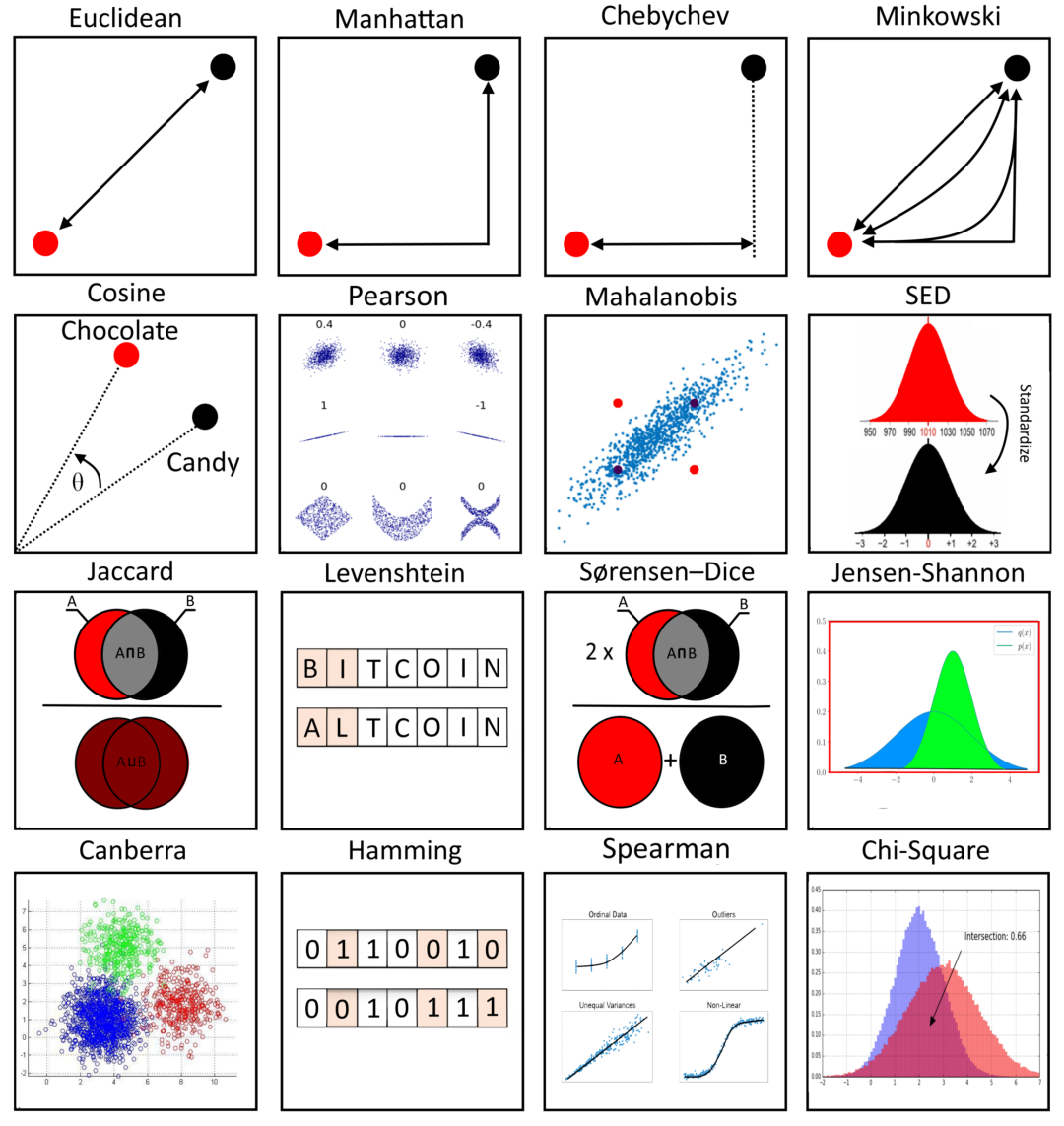
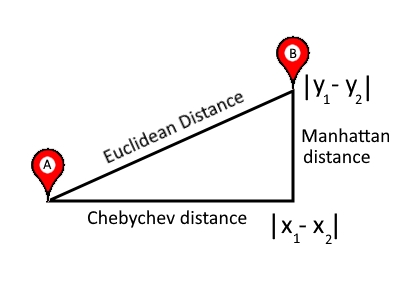
⓪ L2范数，欧几里得距离

用于数值属性或特征的最常见距离函数是欧几里得距离，其定义在以下公式中：
n 维空间中两点之间的欧几里德距离

这个距离度量具有众所周知的特性，例如对称、可微、凸面、球面……

在二维空间中，前面的公式可以表示为：
二维空间中两点之间的欧几里德距离。

它等于直角三角形斜边的长度。

此外，欧几里得距离是一个度量，因为它满足其标准，如下图所示。

此外，使用该公式计算的距离表示每对点之间的最小距离。换句话说，它是从A点到B点的最短路径（二维笛卡尔坐标系），如下图所示：

因此，当你想在路径上没有障碍物的情况下计算两点之间的距离时，使用此公式很有用。这可以认为是你不想计算欧几里德距离的情况之一；而你希望使用其他指标，例如曼哈顿距离，这将在本文稍后将对此进行解释。

欧氏距离无法为我们提供有用信息的另一种情况是，飞机的飞行路径遵循地球的曲率，而不是直线（除非地球是平的，否则不是）。

但是，解释一下如何在机器学习的中使用欧几里德距离。

最著名的分类算法之一 -- KNN 算法，该算法使用欧几里德距离对数据进行分类。为了演示 KNN 如何使用欧几里德度量，我们选择了一个 Scipy 包的流行 iris 数据集。

该数据集包含三种花：Iris-Setosa、Iris-Versicolor 和 Iris-Virginica，并具有以下四个特征：萼片长度、萼片宽度、花瓣长度、花瓣宽度。因此就有一个 4 维空间，在其中表示每个数据点。

为了满足简单和演示目的，我们只选择两个特征：花瓣长度、花瓣宽度和不包括 Iris-virginica 数据。通过这种方式，我们可以在二维空间中绘制数据点，其中 x 轴和 y 轴分别表示花瓣长度和花瓣宽度。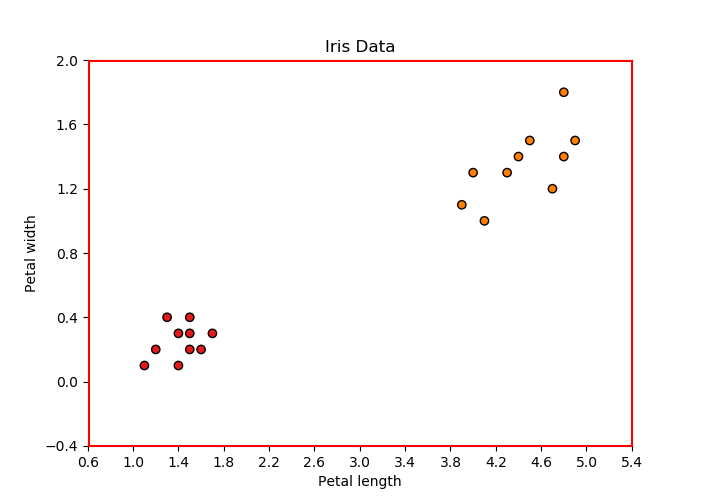

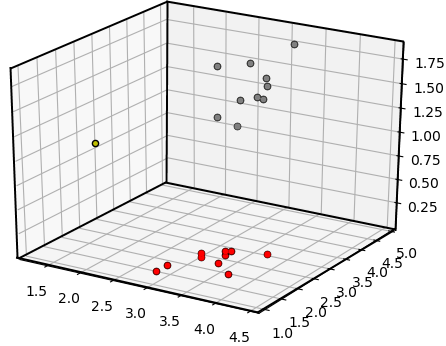
每个数据点都有自己的标签：Iris-Setosa 或 Iris-versicolor（数据集中的 0 和 1）。因此，该数据集可用于 KNN 分类，因为它本质上是一种有监督的 ML 算法。假设我们的 ML 模型（k = 4 的 KNN）已经在这个数据集上进行了训练，我们选择了两个输入特征只有 20 个数据点，如上图所示。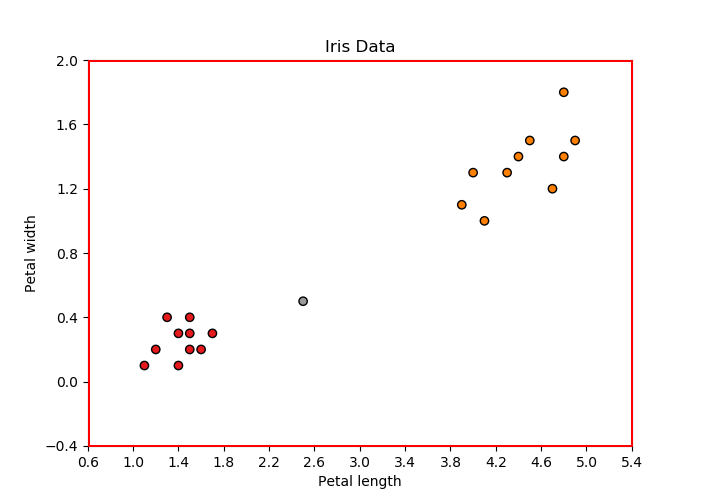

到目前为止，KNN 分类器已准备好对新数据点进行分类。因此，要一种方法来让模型决定新数据点可以分类的位置。

选择欧几里得距离是为了让每个经过训练的数据点投票给新数据样本适合的位置：Iris-Setosa 或 Iris-versicolor。至此，新数据点到我们训练数据的每个点的欧几里德距离都计算出来了，如下图所示：

当k = 4时，KNN分类器需要选择最小的四个距离，代表新点到以下点的距离：point1、point5、point8和point9，如图所示：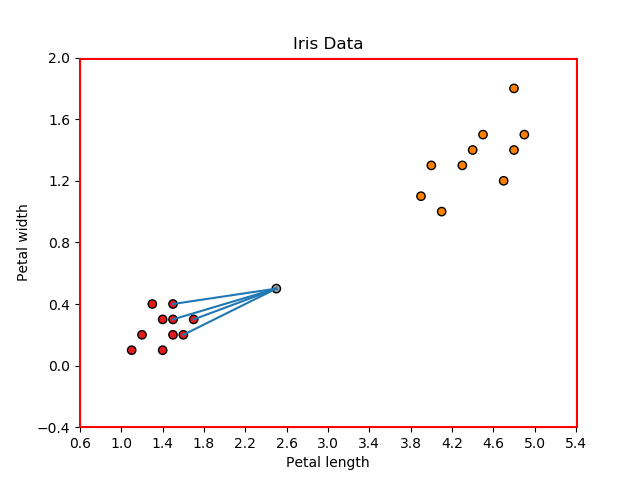

因此，新的数据样本被归类为 Iris-Setosa。使用这个类比，可以想象更高的维度和其他分类器。

如前所述，每个域都需要一种计算距离的特定方法。

➀ 平方欧几里得距离

顾名思义，平方欧几里得距离等于欧几里得距离的平方。因此，平方欧几里得距离可以在计算观测之间的距离的同时减少计算工作。例如，它可以用于聚类、分类、图像处理和其他领域。使用这种方法计算距离避免了使用平方根函数的需要。

n维空间中两点之间的平方欧几里得距离

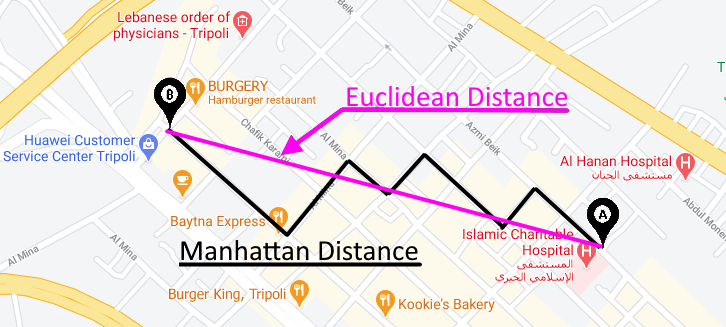
② L1 范数、城市街区、曼哈顿或出租车距离

该指标对于测量给定城市中两条街道之间的距离非常有用，可以根据分隔两个不同地方的街区数量来测量距离。例如，根据下图，A 点和 B 点之间的距离大致等于 4。

创建此方法是为了解决计算给定城市中源和目的地之间的距离的问题，在该城市中，几乎不可能直线移动，因为建筑物被分组到一个网格中，阻碍了直线路径。因此得名城市街区。

你可以说 A 和 B 之间的距离是欧几里得距离。但是，你可能会注意到这个距离没有用。例如，你需要有一个有用的距离来估计旅行时间或需要开车多长时间。相反，如果你知道并选择街道的最短路径，这会有所帮助。因此，这取决于如何定义和使用距离的情况。

n维空间中两点之间的曼哈顿距离表示为：

对于二维网格，二维空间中两点之间的曼哈顿距离公式可以写成：

回忆之前的 KNN 示例，计算从新数据点到训练数据的曼哈顿距离将产生以下值：

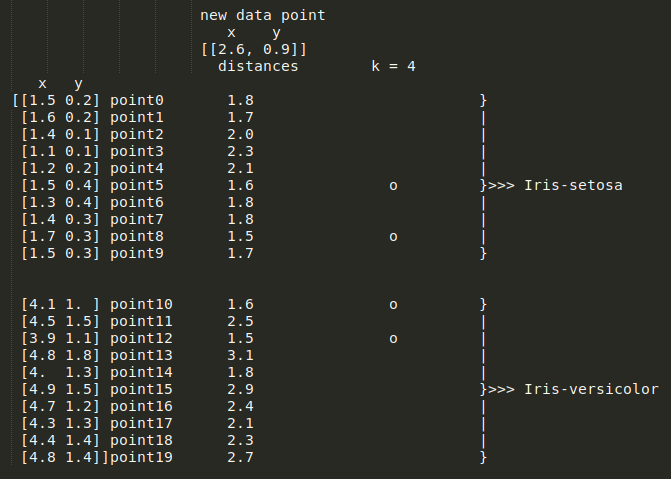
显而易见，有两个数据点投票支持 Iris-Setosa，另外两个数据点投票支持 Iris-versicolor，这意味着这是个平局。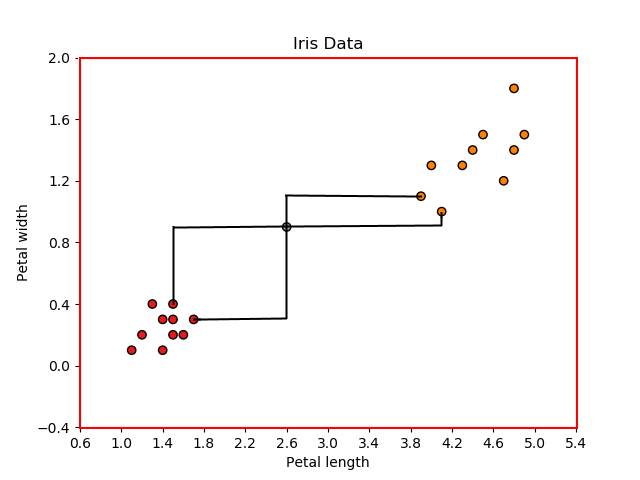

你可能在某个地方遇到过这个问题，一个直观的解决方案是改变 k 的值，如果 k 大于 1，则减少 1，否则增加 1。

但是，对于之前的每个解决方案，将获得 KNN 分类器的不同行为。例如，在我们的示例中，k=4,将其更改为 k=3将导致以下值：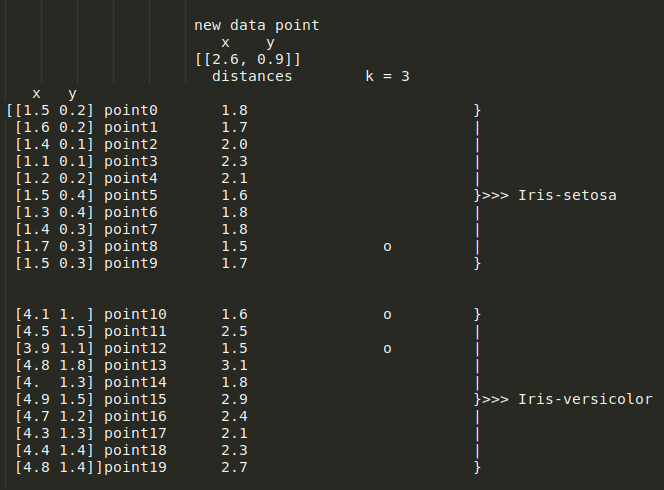

将 k 减少 1

这种花被归类为花斑鸢尾。以同样的方式，将其更改为 k=5 将导致以下值：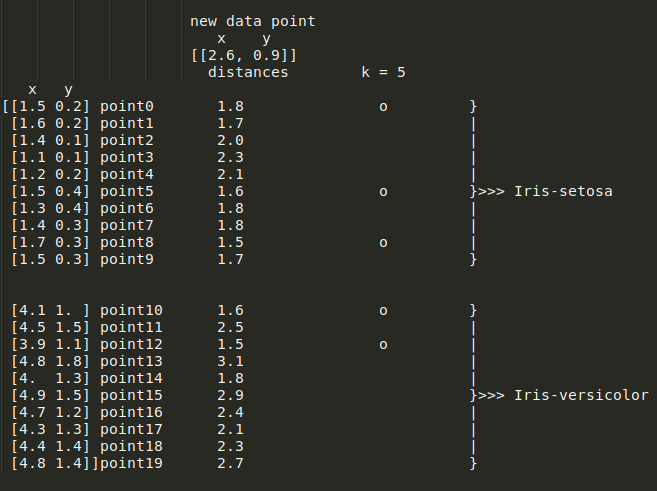

将 k 增加 1

这种花被归类为Iris-Setosa。因此，由你决定是否需要增加或减少 k 的值。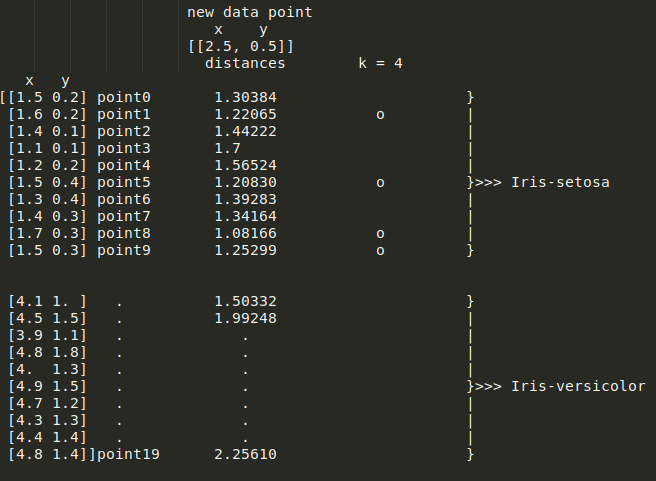

但是，有人会争辩说，如果度量标准不是问题的约束条件，你可以更改它。例如，计算欧几里得距离可以解决这个问题：

这种花被强烈归类为 Iris-Setosa。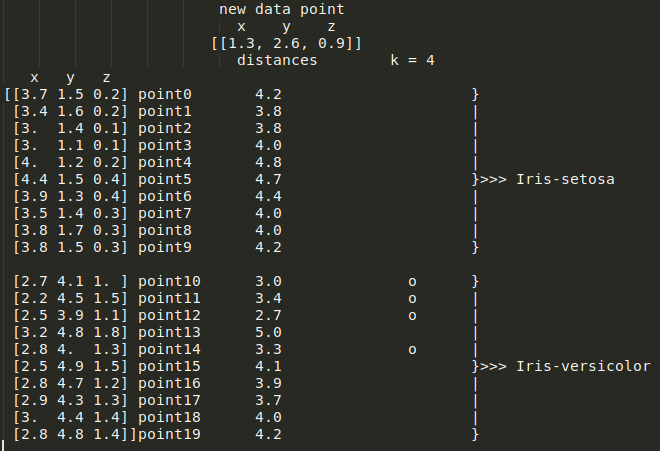

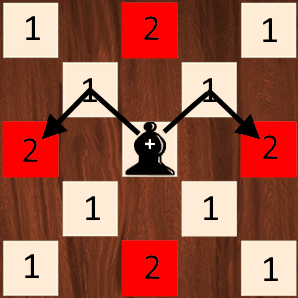
在我看来，如果你不必更改曼哈顿距离并对 k 使用相同的值，那么添加新维度或特征（如果可用）也会打破平局。例如，将萼片宽度添加为新尺寸会导致以下结果：

这种花被归类为杂色鸢尾。

这是 3-D 空间中的图，其中 x 轴、y 轴和 z 轴分别代表萼片宽度、花瓣长度和花瓣宽度：

计算曼哈顿距离比前两种方法计算速度更快。如公式所示，它只需要加减运算，结果证明这比计算平方根和 2 的幂要快得多。

国际象棋中主教使用曼哈顿距离在两个相同颜色的水平或垂直块之间移动：

Bishop 使用曼哈顿距离（如果没有看到，可通过将棋盘旋转 45° 来想象一下）。换句话说，让主教越过红色方块所需的移动次数（距离）等于曼哈顿距离，即 2。

除此之外，如果数据存在许多异常值，曼哈顿距离将优于欧几里得距离。

L1-norm 比 l2-norm 给出更稀疏的估计。除此之外，L1 范数和L2 范数通常用于神经网络的正则化，以最小化权重或将某些值归零，就像套索回归中使用的那样。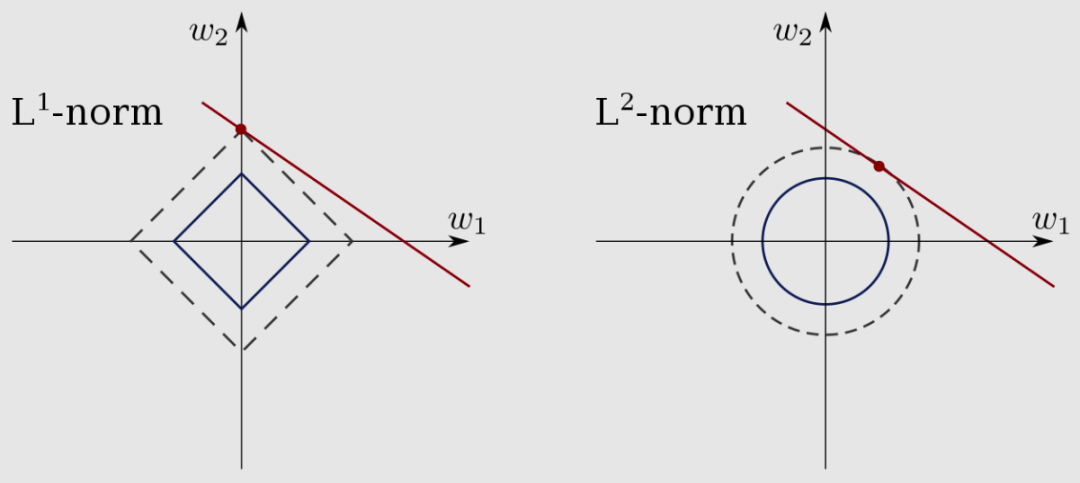

套索和岭回归的约束区域的形式（来源：[维基百科](https://en.wikipedia.org/wiki/Lasso_(statistics "维基百科")#/media/File:L1_and_L2_balls.svg)）。

如上图所示，L1-norm 尝试将 W1 权重归零并最小化另一个权重。然而，L2 范数试图最小化 W1 和 W2 的权重（如 W1 = W2）。

这篇文章深入探讨正则化，它的主要目标是解释常见的距离函数，同时在这里说明一些用法并使其尽可能易于理解。

③ 堪培拉距离

它是聚类中使用的曼哈顿距离的加权版本，如模糊聚类、分类、计算机安全^[2]和火腿/垃圾邮件检测系统。与之前的指标相比，它对异常值的鲁棒性更强。

④ L∞ 范数，切比雪夫距离，最大距离

两个 n维 观测值或向量之间的切比雪夫距离(Chebyshev)等于数据样本坐标之间变化的最大绝对值。在二维世界中，数据点之间的切比雪夫距离可以确定为其二维坐标的绝对差之和。

两点 P 和 Q 之间的切比雪夫距离定义为：

切比雪夫距离是一个度量，因为它满足成为度量的四个条件。

但是，你可能想知道 min 函数是否也可以是一个指标！

min 函数不是度量标准，因为有一个反例（例如水平线或垂直线），其中  且 。但是，仅当  时它才应为零！

你可以想到的使用切比雪夫距离指标的用例之一是交易股票、加密货币，其特征是交易量、买入价、卖出价……

例如，你需要找到一种方法来告诉大多数加密货币在奖励之间有很大差距和损失。而切比雪夫距离非常适合这种特殊情况。

在棋盘中使用切比雪夫距离的另一种常见场景，其中国王或王后的移动次数等于到达相邻方格的距离，如下图所示：

⑤ Lp 范数，闵可夫斯基距离

闵可夫斯基（Minkowski）距离只是之前距离度量的概括：欧几里得、曼哈顿和切比雪夫。它被定义为 n维空间中两个观测值之间的距离，如以下公式所示：

其中 P、Q 是两个给定的 nD 点，p 代表 Minkowski 度量。对于特定的 p 值，您可以得出以下指标：

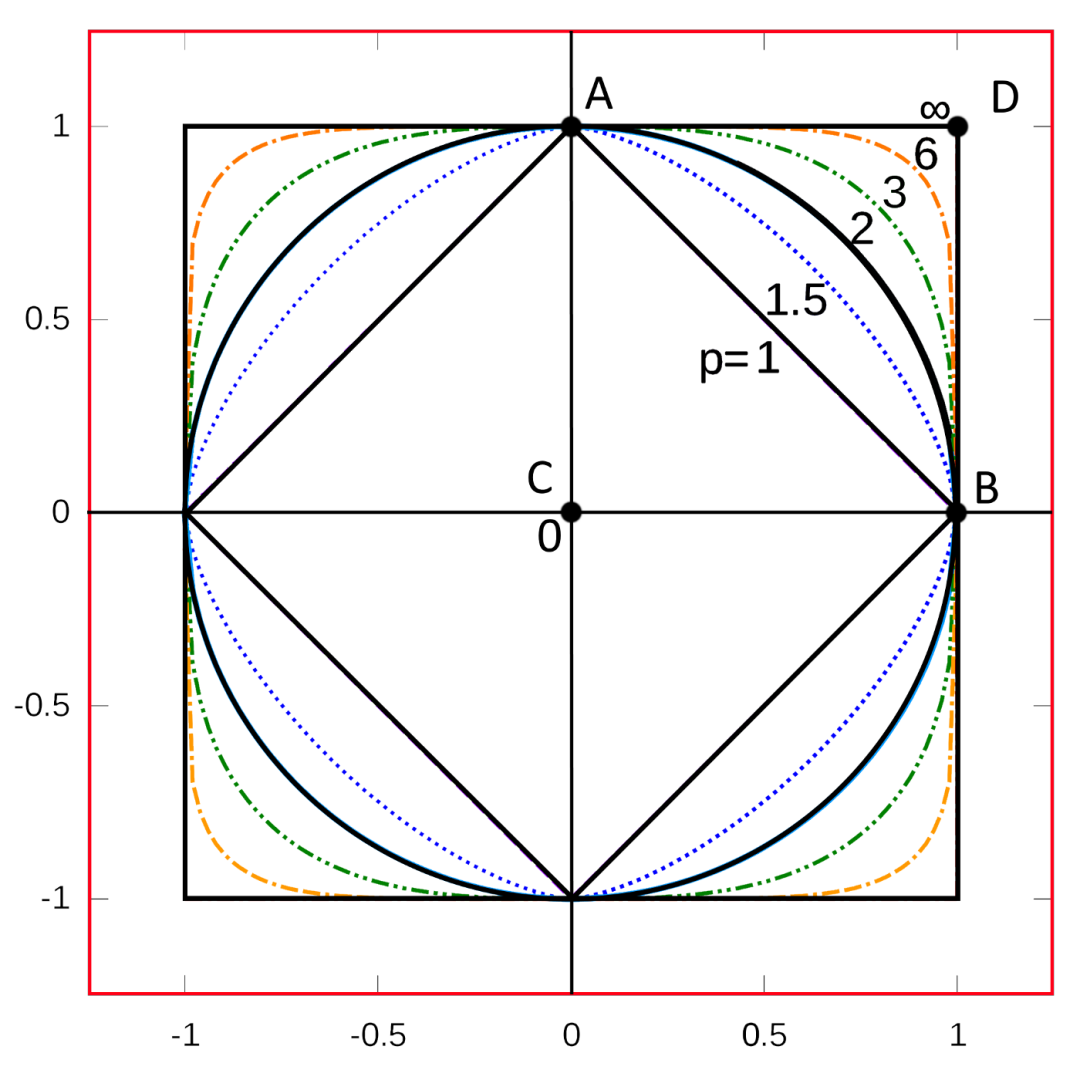
• p = 1： 曼哈顿距离。
• p = 2： 欧几里得距离。
• p → +∞ ： 切比雪夫距离，逻辑或（点 D = A或B = 1或1 = 1）。
• p → 0： 逻辑与（点 C = A AND B = 零）。
• p → -∞ ： 最小距离（点 D 的对称性）。

 ⑥余弦距离

该指标广泛用于文本挖掘、自然语言处理和信息检索系统。例如，它可用于衡量两个给定文档之间的相似性。它还可用于根据消息的长度识别垃圾邮件。

余弦距离可以按如下方式测量：

其中 P 和 Q 代表两个给定的点。这两个点可以表示文档中单词的频率，下面的例子中解释了这一点。

例如，以包含以下短语的三个文档为例：

• 文件A： "I love to drink coffee in the morning."
• 文件B： "I like to drink coffee."
• 文件C： "My friend and I work at a coffee shop in our hometown. He tells some good jokes in the morning. We like to begin the day by drink a cup of tea each."

计算每个单词的频率，出现次数将导致以下结果：

在计算出现次数之前，你已经先验地知道文档 A 和 B 在含义上非常相似：“I love to drink coffee” 然而，文件 C 包含文件 A 的所有单词，但从频率表中的含义非常不同。为了解决这个问题，你需要计算余弦相似度来判断它们是否相似。

一方面，这可以说明信息检索或搜索引擎是如何工作的。将文档 A 视为对给定源（图像、文本、视频……）的查询（短消息），将文档 C 视为需要获取并作为查询响应返回的网页。

另一方面，欧几里得距离无法给出短文档和大文档之间的正确距离，因为在这种情况下它会很大。使用余弦相似度公式将计算两个文档在方向而非大小方面的差异。

为了说明这一点，以下两个文件为例：

• 文件 A： "Bitcoin Bitcoin Bitcoin Money"
• 文件 B： "Money Money Bitcoin Bitcoin"

用“Bitcoin”这个词作为 x 轴，把“Money”这个词作为 y 轴。这意味着文档 A 可以表示为向量 A(3,1)，文档 B 可以表示为 B(2,2)。

计算余弦相似度将得到以下值：

Cosine_Similarity = 0.894 意味着文档 A 和 B 非常相似。cos(angle)大于(接近1)表示角度小(26.6°)，两个文档A和B彼此接近。

但是，你不能将余弦相似度的值解释为百分比。例如，值 0.894 并不意味着文档 A 是 89.4%，与 B 相似。它意味着文档 A 和 B 非常相似，但我们不知道有多少百分比！该值没有阈值。换句话说，你可以将余弦相似度的值解释如下：

它越大，文档 A 和 B 相似的可能性就越大，反之亦然。

再举一个 A(1, 11) 和 B(22, 3) 的例子

计算余弦相似度:

然而，欧几里得距离会给出一个很大的数字，比如 22.4，这并不能说明向量之间的相对相似性。另一方面，余弦相似度也适用于更高维度。

余弦相似度的另一个有趣应用是OpenPose^[3]项目。

参考资料

[1] 

参考原文: https://towardsdatascience.com/17-types-of-similarity-and-dissimilarity-measures-used-in-data-science-3eb914d2681

[2] 

计算机安全: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.97.2974&rep=rep1&type=pdf

[3] 

OpenPose: https://github.com/CMU-Perceptual-Computing-Lab/openpose

点击下方卡片进行关注，获取更多内容

点分享

点收藏

点点赞

点在看