通俗易懂理解朴素贝叶斯分类的拉普拉斯平滑
点击上方“小白学视觉”,选择加"星标"或“置顶”
重磅干货,第一时间送达
这个男生的四个特征是长相不帅,性格不好,身高矮,不上进,我们最终得出的结论是女生不嫁!很多人说这是一道送分题,哈哈哈哈。我们用数学算法也说明了不靠谱是取不到老婆滴!
那么我们再来一个例子,假如此时另外一对情侣,这对情侣中,男生的四个特征是,长相帅,性格爆好,身高高,上进,那么他的女朋友嫁还是不嫁呢?可能又会有小伙伴说这是一道送分题,是不是,我们下面用事实说话!
下面通过例子来引出拉普拉斯平滑过程!
还是下面的训练数据:
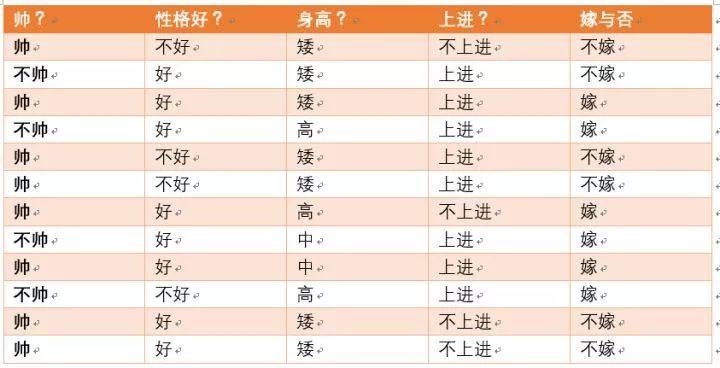
四个特征集合分别长相{帅,不帅}、性格{爆好,好,不好}、身高{高,中,矮}、上进与否{上进,不上进}
我们此时要求出该男生在四个特征分别是长相帅,性格爆好,身高高,上进的情况下,他对应的嫁与不嫁的概率谁大谁小,从而得出结论!
也就是要比较p(嫁|长相帅,性格爆好,身高高,上进)与p(不嫁|长相帅,性格爆好,身高高,上进)的概率大小。
按照朴素贝叶斯算法公式,我们可以得到如下公式:

由于两者的分母都是p(长相帅)、p(性格爆好)、p(身高高)、p(上进),那么我们可以不算分母,比较的时候只比较俩个公式分子大小即可。
好的,下面我们开始计算,先计算在四个特征的条件下,嫁的概率。
我们需要分别计算p(性格爆好|嫁)、p(长相帅|嫁)、p(身高高|嫁)、p(上进|嫁)
首先我们来算p(性格爆好|嫁)=?我们观察训练数据,发现如下:

居然没有一个数据有爆好这个特点的,那么p(性格爆好|嫁) = 0,那么我们可以看出问题了,根据公式:

我们最后的p(嫁|长相帅、性格爆好、身高高、上进)由于一项p(性格爆好|嫁)为0,而造成整个概率为0,这显然是错误的。
而这个错误的造成是由于训练量不足,会令分类器质量大大降低。为了解决这个问题,我们引入Laplace校准(这就引出了我们的拉普拉斯平滑),它的思想非常简单,就是对每个类别下所有划分的计数加1,这样如果训练样本集数量充分大时,并不会对结果产生影响,并且解决了上述频率为0的尴尬局面。
引入拉普拉斯平滑的公式如下:
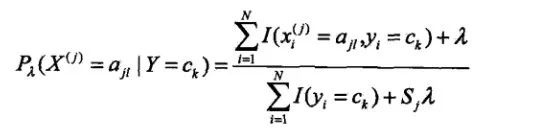
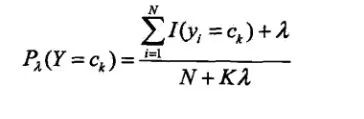
其中ajl,代表第j个特征的第l个选择,Sj代表第j个特征的个数,K代表种类的个数。
λ为1,这也很好理解,加入拉普拉斯平滑之后,避免了出现概率为0的情况,又保证了每个值都在0到1的范围内,又保证了最终和为1的概率性质!
我们可以通过下面例子更加深刻的理解这个公式:(现在我们是加入拉普拉斯平滑)
我们先需要分别计算p(性格爆好|嫁)、p(长相帅|嫁)、p(身高高|嫁)、p(上进|嫁),p(嫁)
p(性格爆好|嫁)=?统计满足要求的如下面红色部分

没有一个满足是性格爆好的条件,但是此时概率不为0,按照加入拉普拉斯平滑后的公式,性格特征的个数为爆好,好,不好,三种情况,那么Sj为3,则最终概率为1/9 (嫁的个数为6+特征个数为3)
p(长相帅|嫁)=?统计满足条件的如下面红色部分:
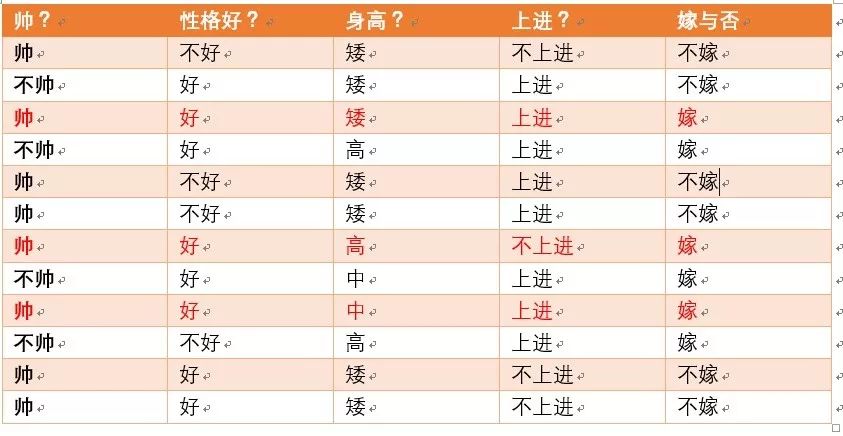
由上图可知满足要求的为3个,按照加入拉普拉斯平滑后的公式,长相特征的个数为帅,不帅,两种情况,那么Sj为2,则最终概率p(长相帅|嫁)为4/8 (嫁的个数为6+特征个数为2)
p(身高高|嫁) = ?统计满足条件的如下面红色部分:
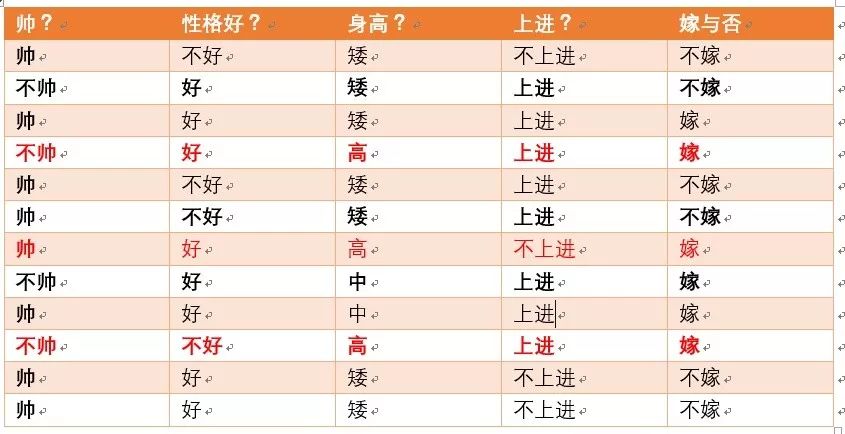
由上图可知满足要求的为3个,按照加入拉普拉斯平滑后的公式,身高特征的个数为高,中,矮情况,那么Sj为3,则最终概率p(身高高|嫁)为4/9 (嫁的个数为6+特征个数为3)
p(上进|嫁)=?统计满足要求的如下面红色部分:
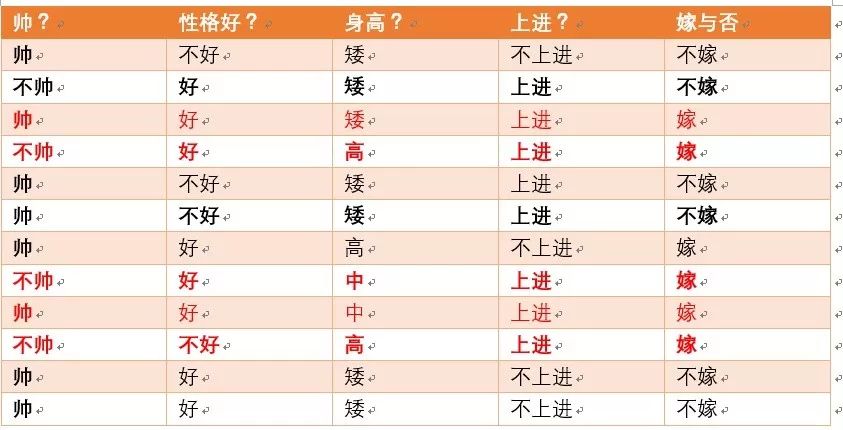
由上图可知满足要求的为5个,按照加入拉普拉斯平滑后的公式,上进特征的个数为上进,不上进情况,那么Sj为2,则最终概率p(上进|嫁)为6/8 (嫁的个数为6+特征个数为2)
p(嫁) = ?满足要求的如下红色标注:
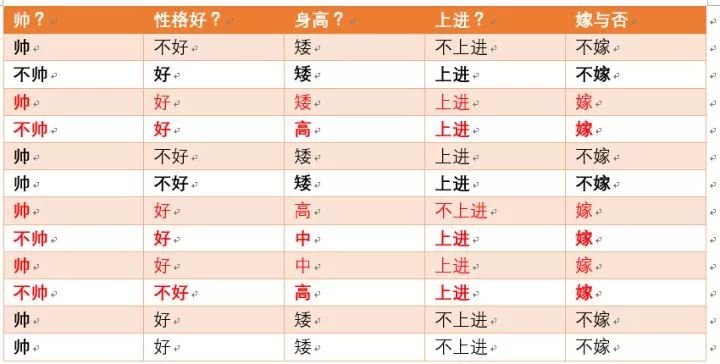
由上图可知满足要求的为6个,按照加入拉普拉斯平滑后的公式,种类的个数为嫁,不嫁情况,那么K为2,则最终概率p(嫁)为7/14 = 1/2 (嫁的个数为6+种类个数为2)
到这里为止,我们已经算出了在该男生条件下,嫁的概率为:
p(嫁|长相帅、性格爆好、身高高、上进) = 1/9*4/8*4/9*6/8*1/2
下面我们需要算出p(不嫁|长相帅、性格爆好、身高高、上进)的概率,然后与上面的数值进行比较即可,算法与上面完全一模一样!这里也走一遍。
我们需要估计出p(长相帅|不嫁)、p(性格爆好|不嫁)、p(身高高|不嫁)、p(上进|不嫁),p(不嫁)的概率分别为多少。
p(长相帅|不嫁)=?满足要求如下面红色标注:
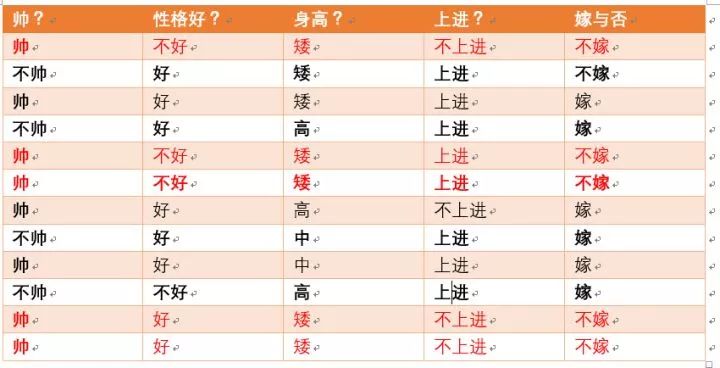
由上图可知满足要求的为5个,按照加入拉普拉斯平滑后的公式,长相帅特征的个数为不帅,帅情况,那么Sj为2,则最终概率p(长相不帅|不嫁)为6/8 (不嫁的个数为6+特征个数为2)
p(性格爆好|不嫁)=?满足要求如下面红色标注:
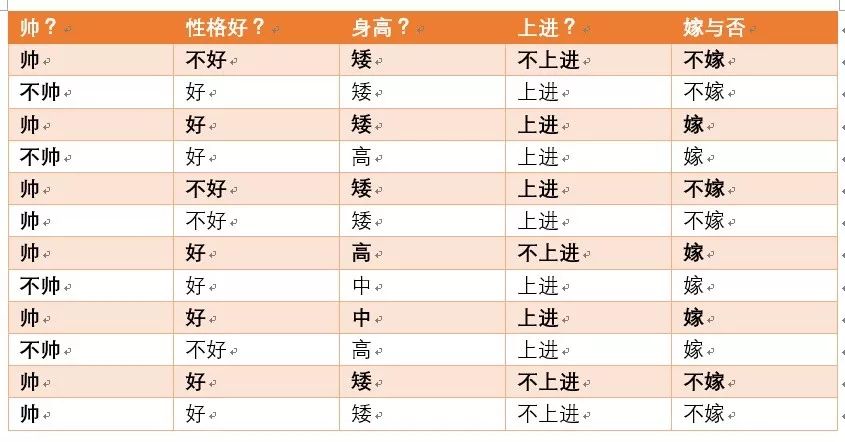
没有一个满足是性格爆好的条件,但是此时概率不为0,按照加入拉普拉斯平滑后的公式,性格特征的个数为爆好,好,不好,三种情况,那么Sj为3,则最终概率p(性格爆好|不嫁)为1/9 (不嫁的个数为6+特征个数为3)
p(身高高|不嫁)=?满足要求如下面红色标注:

没有一个满足是身高高的条件,但是此时概率不为0,按照加入拉普拉斯平滑后的公式,身高特征的个数为高,中,矮,三种情况,那么Sj为3,则最终概率p(身高高|不嫁)为1/9 (不嫁的个数为6+特征个数为3)
p(上进|不嫁)=?满足要求如下面红色标注:
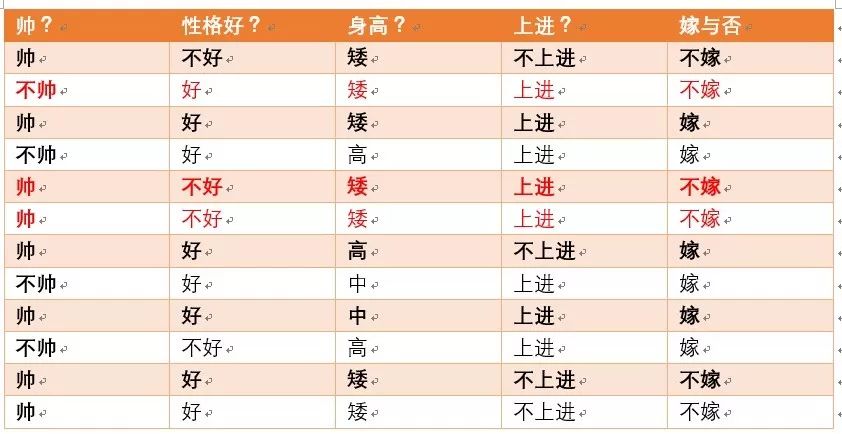
由上图可知满足要求的为3个,按照加入拉普拉斯平滑后的公式,上进特征的个数为上进,不上进情况,那么Sj为2,则最终概率p(上进|不嫁)为4/8 (不嫁的个数为6+特征个数为2)
p(不嫁)=?满足要求的如红色标注:
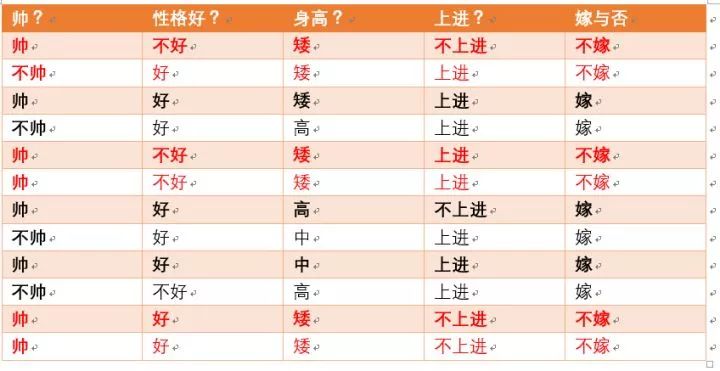
由上图可知满足要求的为6个,按照加入拉普拉斯平滑后的公式,种类的个数为嫁,不嫁情况,那么K为2,则最终概率p(不嫁)为7/14 = 1/2 (不嫁的个数为6+种类个数为2)
到这里为止,我们已经算出了在该男生条件下,不嫁的概率为:
p(不嫁|长相帅、性格爆好、身高高、上进) = 5/8*1/9*1/9*3/8*1/2
于是我们可以得到
p(嫁|长相帅、性格爆好、身高高、上进) = 1/9*4/8*4/9*6/8*1/2 > p(不嫁|长相帅、性格爆好、身高高、上进) = 6/8*1/9*1/9*4/8*1/2
于是我们可以大胆的告诉女生,这样的好男人,贝叶斯告诉你了,该嫁!!!
这就是我们使用拉普拉斯平滑后计算的整个算法过程!
希望对大家的理解有帮助~欢迎大家指错交流!
好消息!
小白学视觉知识星球
开始面向外开放啦👇👇👇
下载1:OpenCV-Contrib扩展模块中文版教程 在「小白学视觉」公众号后台回复:扩展模块中文教程,即可下载全网第一份OpenCV扩展模块教程中文版,涵盖扩展模块安装、SFM算法、立体视觉、目标跟踪、生物视觉、超分辨率处理等二十多章内容。 下载2:Python视觉实战项目52讲 在「小白学视觉」公众号后台回复:Python视觉实战项目,即可下载包括图像分割、口罩检测、车道线检测、车辆计数、添加眼线、车牌识别、字符识别、情绪检测、文本内容提取、面部识别等31个视觉实战项目,助力快速学校计算机视觉。 下载3:OpenCV实战项目20讲 在「小白学视觉」公众号后台回复:OpenCV实战项目20讲,即可下载含有20个基于OpenCV实现20个实战项目,实现OpenCV学习进阶。 交流群
欢迎加入公众号读者群一起和同行交流,目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群(以后会逐渐细分),请扫描下面微信号加群,备注:”昵称+学校/公司+研究方向“,例如:”张三 + 上海交大 + 视觉SLAM“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告,否则会请出群,谢谢理解~

