拉普拉斯变换的本质意义（通俗易懂的好文）

本文将从通俗的角度看待拉普拉斯变换。

发明者

奥列弗.赫维赛德，维多利亚时期英国人，全靠自学，听力残疾。很多人熟悉赫维赛德是因为MATLAB有一个赫维赛德（Heaviside）函数。

赫维赛德简化了麦克斯韦方程组：即变化的电场产生磁场，变化的磁场产生电场。让20个方程组便成了4个。

**赫维赛德另一个贡献就是我们今天要说的运算微积分-它可以将常微分方程转换为普通代数方程。**赫维赛德是怎么解微分方程的呢？他把微分、积分运算用一个简单的算子来代替。

也就是说，在某种算子下，积分和微分对应的是倒数关系，至于算子 p 代表什么，赫维赛德也没有多解释，在缺乏严密数学基础的情况下，人家直接放在文章就用了，还发表了。比如常见的一个二阶常微分方程，

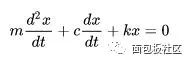
如果用赫维赛德的微分算子变换一下，就变成了代数表达式。

赫维赛德之所以这么做，是因为他的“物理直觉”告诉他这么做，就是这么硬。这显然是一种开外挂的行为，因此也受到当时的主流数学家们们的攻讦，他们认为赫维赛德就是十足的“民科”，文章没什么理论依据，自己在那空想呢。当然，赫维赛德也不是弱鸡，科学家怼起人来，也是毫不含糊：“因为我不能理解消化过程就拒绝晚餐吗？不，只要我满意这个结果。”

好了，扯了那么远，有童鞋已经不耐心了：这些和拉普拉斯变换有什么关系？谜底就是：赫维赛德的微积分算子，就是拉普拉斯变换的前身。

傅里叶变换（轻量版拉普拉斯变换）

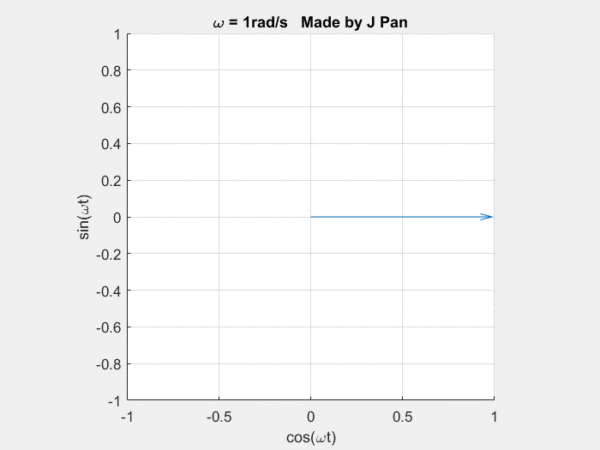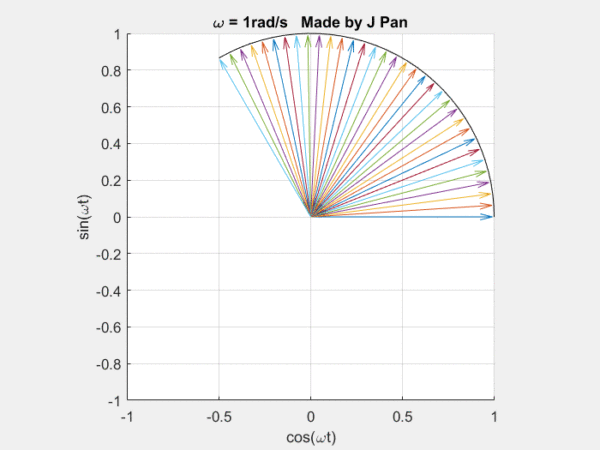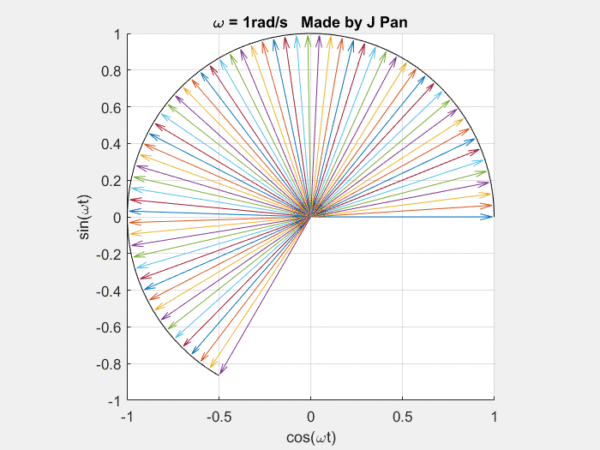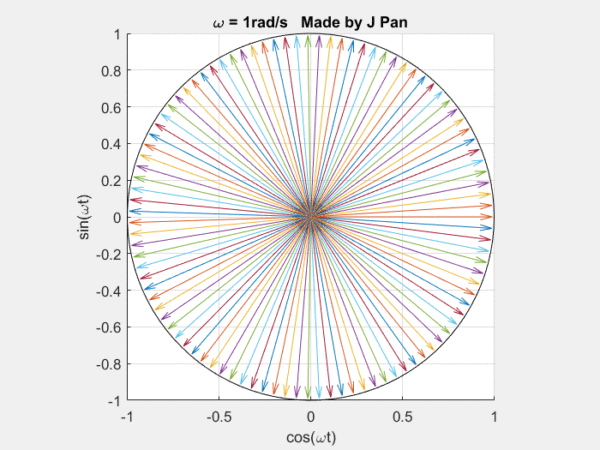
在说拉普拉斯变换以前，我们要先提一下傅里叶变换，这可以看成是轻量版的拉普拉斯变换。傅里叶变换说的是什么事？说的是自然界的很多现象，都可以用三角函数进行分解。

clc;clear;
h = animatedline;
xl=xlabel('cos(\omegat)');% 
yl=ylabel('sin(\omegat)');% 
grid on;
title('\omega = 1rad/s   Made by J Pan')
axis([-1,1,-1,1]);
axis square;
N = 100;
t=linspace(0,2*pi,N);
w=1;
x=cos(w*t);
y=sin(w*t);
a = tic; % start timer
for k = 1:N
    addpoints(h,x(k),y(k));
    hold on
    quiver(0,0,x(k)*1.1,y(k)*1.1)
    b = toc(a); % check timer
    if b > (1/90)
        drawnow % update screen every 1/30 seconds
        a = tic; % reset timer after updating
    end
end

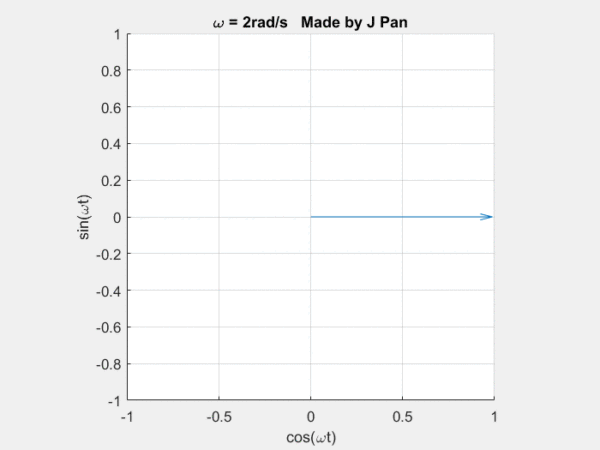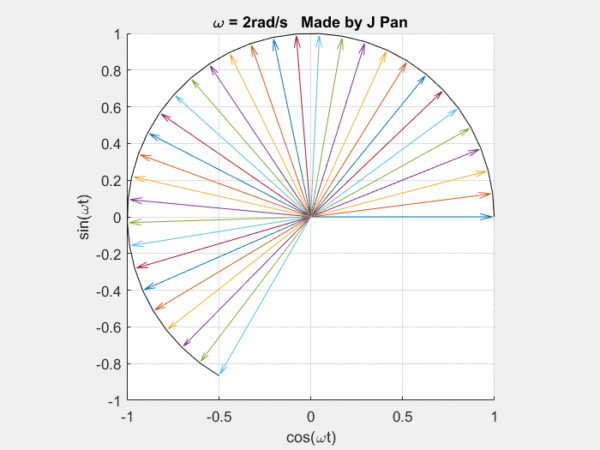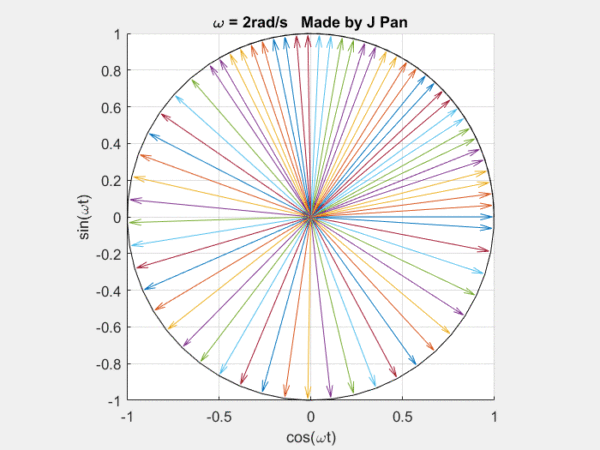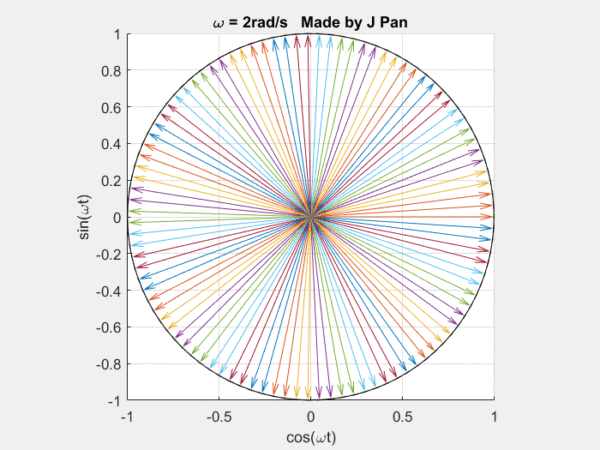
你能想象到很多曲线，都可以用这些不同频率，连续旋转的圆，通过线性叠加得到，而傅里叶定律，就是对这个结论的数学描述。

傅里叶定律说：只要一个函数满足如狄利赫里条件，都能分解为复指数函数之和，哪怕是如拉格朗日提到的带有棱角的方波函数。狄利赫里条件为：

其中可去间断点和跳跃间断点属于第一类间断点

于是就可以很好的解释拉格朗日和傅里叶之间的争论了——拉格朗日是对的：正弦曲线无法组合成一个带有棱角的信号，棱角处会有很小高频波动（吉布斯现象）。但是，我们可以用正弦曲线来非常逼近地表示它，逼近到两种表示方法不存在能量差别，基于此，傅里叶也是对的。一个从数学家的角度，一个从工程师的角度。

拉普拉斯变换-原来就是这么回事

傅里叶变换能帮我们解决很多问题，一经问世后便受到广大工程师们的喜爱，因为它给人们提供了一扇不同的窗户来观察世界，从这个窗户来看，很多事情往往变得简单多了。但是，别忘了，傅里叶变换有一个很大局限性，那就是信号必须满足狄利赫里条件才行，特别是那个绝对可积的条件，一下子就拦截掉了一大批函数。比如函数 f(t)=t^2 就无法进行傅里叶变换。这点难度当然拿不到聪明的数学家们，他们想到了一个绝佳的主意：把不满足绝对的可积的函数乘以一个快速衰减的函数，这样在趋于无穷 时原函数也衰减到零了，从而满足绝对可积。

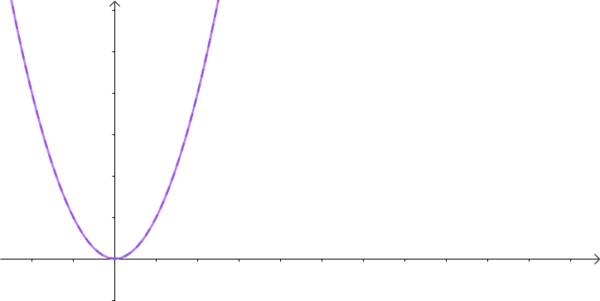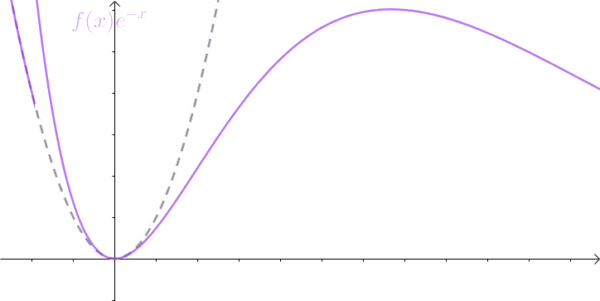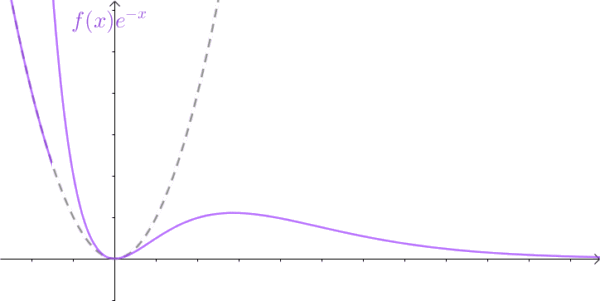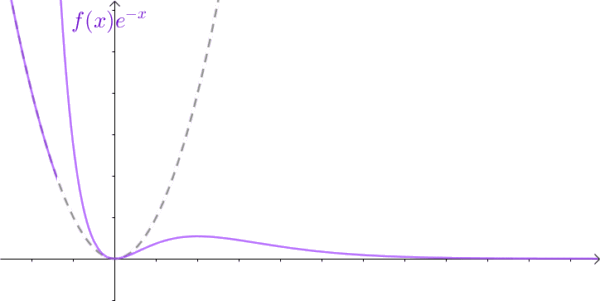
这里我要补充一下，不是为了保证一直为衰减，指数函数，要衰减，在负半轴也是衰减的，要增加，在正负半轴都是增加的。是因为在我们关心的系统中，不对时间的负半轴作分析。因此，我们更多使用单边的拉普拉斯变换，而不是使用双边的拉普拉斯变换，这样的系统称之为因果系统不需要考虑 t=0 时的系统初始条件。

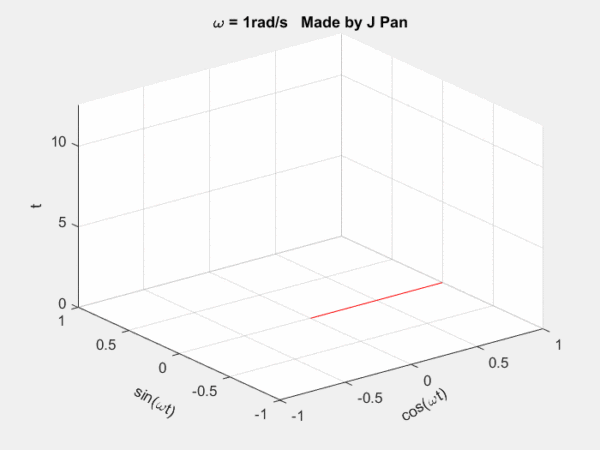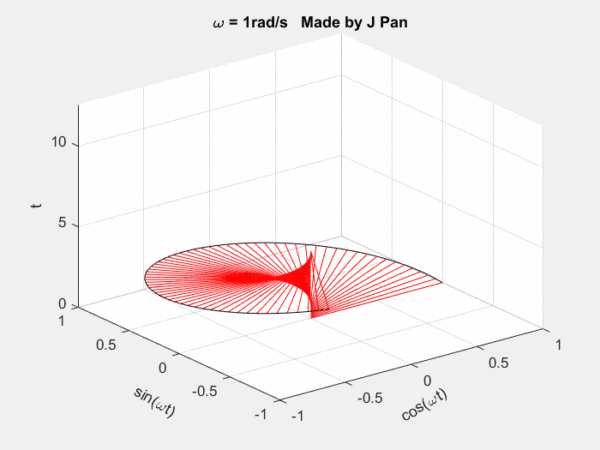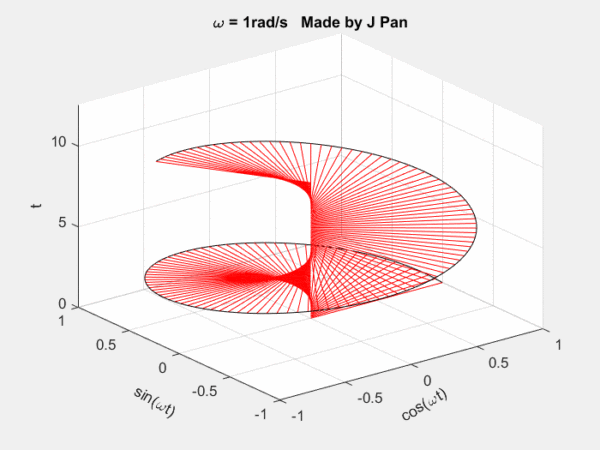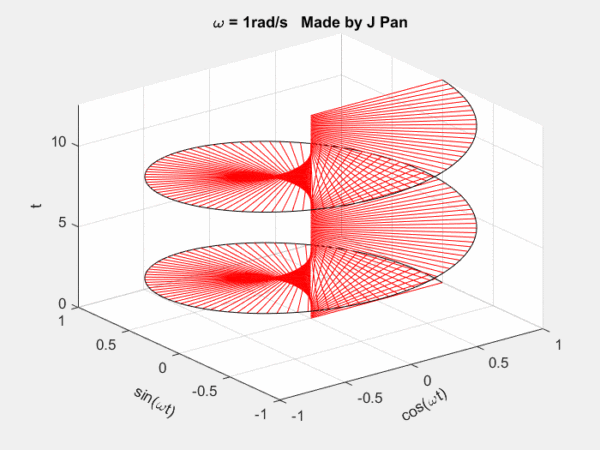
我知道大部分人前面的数学推导没什么兴趣，接下来就是放彩蛋的时刻了，很多童鞋会说不管傅里叶变换或者拉普拉斯变换是什么细节，你能说点有意思的，让人能记忆深刻的信息吗？

clc;clear;
h = animatedline;
h1=gcf;
view(3);
xl=xlabel('cos(\omegat)');% 
yl=ylabel('sin(\omegat)');% 
zl=zlabel('t');% 
set(xl,'Rotation',30);% 
set(yl,'Rotation',-30);%
grid on;
title('\omega = 1rad/s   Made by J Pan')
axis([-1,1,-1,1,0,4*pi])
N = 200;
t=linspace(0,4*pi,N);
w=1;
x=cos(w*t);
y=sin(w*t);
a = tic; % start timer
for k = 1:N
    addpoints(h,x(k),y(k),t(k));
    hold on
    line([0 x(k)],[0 y(k)],[t(k) t(k)],'Color','red')
    b = toc(a); % check timer
    if b > (1/90)
        drawnow % update screen every 1/30 seconds
        a = tic; % reset timer after updating
    end
end

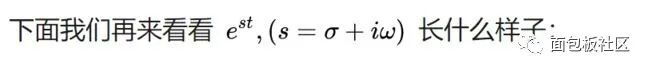
clc;clear;
h = animatedline;
h1=gcf;
view(3);
xl=xlabel('cos(\omegat)');% 
yl=ylabel('sin(\omegat)');% 
zl=zlabel('t');% 
set(xl,'Rotation',30);% 
set(yl,'Rotation',-30);%
grid on;
title('\omega = 1rad/s   Made by J Pan')
axis([-1,1,-1,1,0,4*pi])
N = 200;
t=linspace(0,4*pi,N);
w=1;sig=-0.2;
x=exp(sig*t).*cos(w*t);
y=exp(sig*t).*sin(w*t);
a = tic; % start timer
for k = 1:N
    addpoints(h,x(k),y(k),t(k));
    hold on
    line([0 x(k)],[0 y(k)],[t(k) t(k)],'Color','red')
    b = toc(a); % check timer
    if b > (1/90)
        drawnow % update screen every 1/30 seconds
        a = tic; % reset timer after updating
    end
end

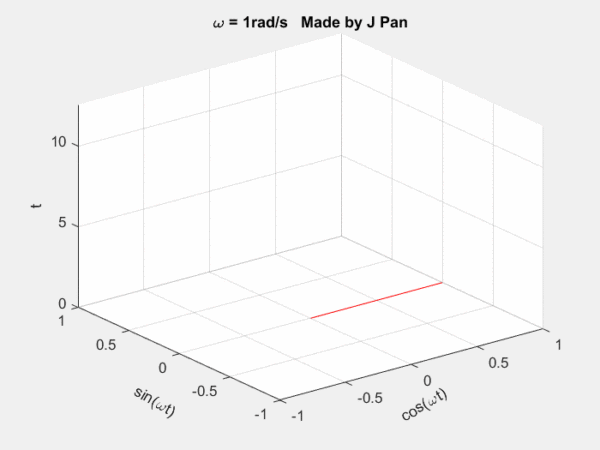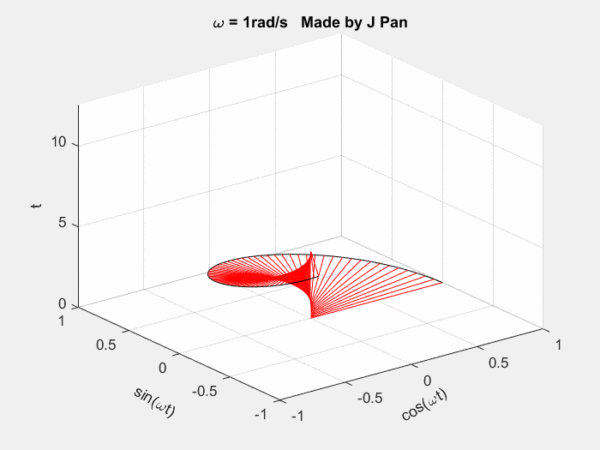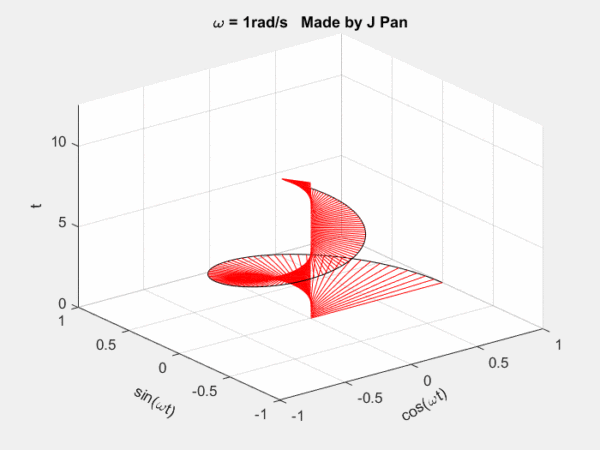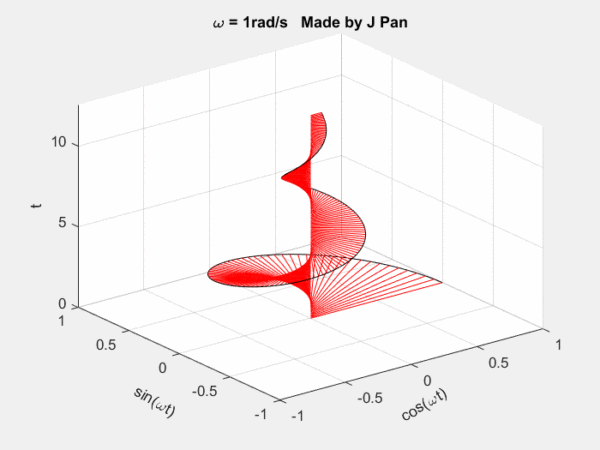
螺旋曲线和衰减函数的乘积：一个半径不断减小的螺旋曲线。从不同的平面看，就是不断衰减的正弦或者余弦曲线，从复平面来看，是一个半径不断减小的圆。

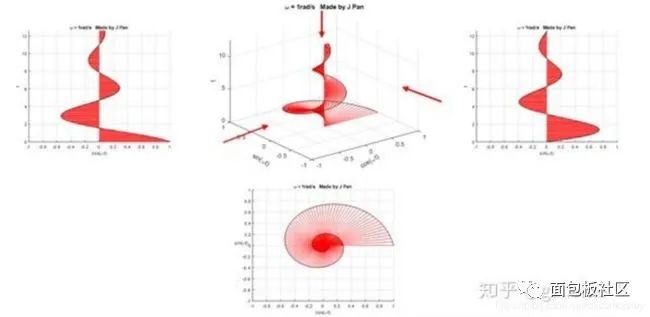
总结一下：傅里叶变换是将函数分解到频率不同、幅值恒为1的单位圆上；拉普拉斯变换是将函数分解到频率幅值都在变化的圆上。因为拉普拉斯变换的基有两个变量，因此更灵活，适用范围更广。

本文大量引用了：https://zhuanlan.zhihu.com/p/40783304

本文仅做学术分享，如有侵权，请联系删文。