SimSiam：孪生网络表征学习的顶级理论解释-技术圈

之前太菜了，SimSiam最精彩的理论解释没完全看懂，元旦重新读了一遍，太牛逼了，我原本以为SimSiam就是BYOL的一个简化版本，实则是孪生网络表征学习的顶级理论解释，剖析出带stop-gradient孪生网络表征学习的本质是EM算法。

为了讲清楚SimSiam和EM算法以及k-means算法有什么内在联系，本文先简单阐述一下EM算法和k-means算法的思想，然后从EM算法出发推导出SimSiam的优化目标，并且通过推导结果解释predictor和momentum encoder(EMA)的作用。

EM

EM算法的全称是Expectation-Maximization，是机器学习中最为经典的算法之一。EM算法可以认为是一种算法思想，其实很多机器学习算法中都用到了EM思想，比如非常经典的k-means聚类算法，等下也会讲到k-means是如何应用EM的。

EM算法可以认为是极大似然估计的拓展，极大似然估计只估计一个变量，而EM算法需要同时估计两个变量。学过概率统计的都知道，直接估计两个变量是很困难的问题，所以EM算法实际上是为了解决多个变量估计困难提出来的算法思想，通过一个迭代的方式，先固定其中一个变量，估计另一个变量，然后交替迭代更新，循环往复直至收敛。一个迭代有两个步骤(分别估计两个变量)，先E步，然后M步(M步其实就是极大似然估计)。

有关EM算法的详细解释可以看文章链接：

https://zhuanlan.zhihu.com/p/36331115

k-means

一个最直观了解 EM 算法思路的是 k-means 算法(一个变量是如何得到聚类中心，另一个变量是如何划分数据)。在 k-means 聚类时，每个聚类簇的中心是隐含数据。我们会假设 K 个初始化中心(初始化中心随机得到，后续迭代中心通过聚类平均进行更新)，即 EM 算法的 E 步；然后计算得到每个样本最近的中心，并把样本聚类到最近的这个中心，即 EM 算法的 M 步。重复这个 E 步和 M 步，直到中心不再变化为止，这样就完成了 k-means 聚类。

SimSiam

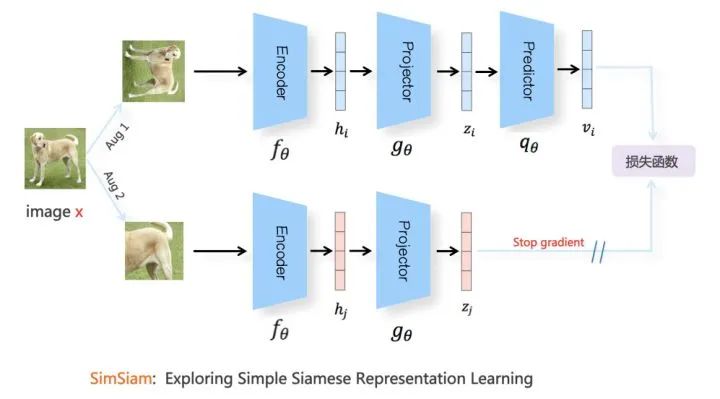
图片来源：https://zhuanlan.zhihu.com/p/367290573

SimSiam也可以用EM算法解释。SimSiam实际上隐式的包含了两个变量，并且同时解决了两个潜在的子问题。实际上stop-gradient操作引入了其中一个变量。

我们可以把SimSiam的损失函数定义成以下形式(这里先不考虑SimSiam的predictor)：

$\mathcal { L } ( \theta , \eta ) = \mathbb { E } _ { x , \mathcal { T } } \left[ \left\| \mathcal { F } _ { \theta } ( \mathcal { T } ( x ) ) - \eta _ { x } \right\| _ { 2 } ^ { 2 } \right]$

其中 $\mathcal { T }$ 表示前面的数据增强函数， $\mathcal { F } _ { \theta }$ 表示Encoder加Projector的网络函数。期望E是关于图像x和数据增强 $\mathcal { T }$ 的分布(也就是所有图片和数据增强的损失期望之和)。为了方便分析，用L2余弦相似度的等价形式MSE来表示相似度。 $\eta _ { x }$ 表示图片x的表征(也就是上图下面分支的输出)。那么优化目标就可以定义成：

$\min _ { \theta , \eta } \mathcal { L } ( \theta , \eta )$

这个优化目标的形式就类似于EM和k-means算法。其中变量 $\theta$ 和聚类中心类似，是encoder和projector的可学习参数；变量 $\eta$ 和采样点x的分配向量类似，是图片x的表征。那么SimSiam可以和k-means算法一样，通过一个EM迭代算法来解决，固定住一个变量，估计另一个变量。形式上可以写成以下两个子问题：

$\begin{aligned} \theta ^ { t } & \leftarrow \arg \min _ { \theta } \mathcal { L } \left( \theta , \eta ^ { t - 1 } \right) \\ \eta ^ { t } & \leftarrow \arg \min _ { \eta } \mathcal { L } \left( \theta ^ { t } , \eta \right) \end{aligned}$

其中t表示迭代轮次， $\leftarrow$ 表示赋值。

可以通过SGD来求解 $\theta ^ { t }$ ，从这个求解式子可知，stop-gradient是必须的操作，试想一下，如果没有stop-gradient，那么 $\eta ^ { t - 1 }$ 就不是一个常数，也就是第一个子问题有两个变量，无法求解。

求解完 $\theta ^ { t }$ 之后，第二个子问题就只剩下一个变量 $\eta$ 。将 $\theta ^ { t }$ 代入损失函数中，第二个子问题就变成了：

$\begin{aligned}\eta ^ { t } & \leftarrow \arg \min _ { \eta } \mathbb { E } _ { \mathcal { T } } \left[ \left\| \mathcal { F } _ { \theta ^ { t } } ( \mathcal { T } ( x ) ) - \eta _ { x } \right\| _ { 2 } ^ { 2 } \right] \end{aligned}$

通过期望公式可得：

$\eta _ { x } ^ { t } \leftarrow \mathbb { E } _ { \mathcal { T } } \left[ \mathcal { F } _ { \theta ^ { t } } ( \mathcal { T } ( x ) ) \right]$

这个式子表示第t个迭代轮次的图片x表征由该图片所有数据增强期望计算得到。

One-step alternation

上述两个子问题的一次step可以近似为SimSiam。

1. 首先，可以用一次采样的数据增强 $\mathcal { T } ^ { \prime }$ 来对第二个子问题进行近似(一次数据增强的期望等于本身)：

$\eta _ { x } ^ { t } \leftarrow \mathcal { F } _ { \theta ^ { t } } \left( \mathcal { T } ^ { \prime } ( x ) \right)$

然后把上式代入第一个子问题中：

$\theta ^ { t + 1 } \leftarrow \arg \min _ { \theta } \mathbb { E } _ { x , \mathcal { T } } \left[ \left\| \mathcal { F } _ { \theta } ( \mathcal { T } ( x ) ) - \mathcal { F } _ { \theta ^ { t } } \left( \mathcal { T } ^ { \prime } ( x ) \right) \right\| _ { 2 } ^ { 2 } \right]$

其中 $\theta ^ { t }$ 是子问题中的一个常数， $\mathcal { T } ^ { \prime }$ 和 $\mathcal { T }$ 表示两个不同的数据增强，于是上式就变成了一个孪生网络结构。

2. 如果上式用一个SGD来降低loss，那么就可以得到接近SimSiam的算法(这里没有考虑SimSiam的predictor，等下解释predictor的作用)：一个使用stop-gradient的孪生网络。

Multi-step alternation

如果把上面一次step拓展到多次step，就可以得到多次step的SimSiam。

多次step的SimSiam可以设计成将t作为迭代的外循环次数，第一个子问题设计成一次迭代k个step SGD(k个step SGD的所有 $\eta _ { x }$ 表征预先计算缓存到内存中)。

上述实验中n-step表示SimSiam一次迭代的step数，1-epoch表示一个epoch中一次迭代总的step数。可以发现，适当的增加SimSiam的一次迭代的step数，可以提升精度(可以认为在一次迭代中变相的增加数据量，从k-means的角度考虑聚类效果会更好)。

Predictor

上述推导为了简便起见，省略了predictor h，如果增加一个predictor h，第二个子问题就变成了：

$\eta _ { x } ^ { t } \leftarrow \mathbb { E } _ { z } \left[ \left\| h \left( z _ { 1 } \right) - z _ { 2 } \right\| _ { 2 } ^ { 2 } \right]$

通过期望公式可得：

$h \left( z _ { 1 } \right) = \mathbb { E } _ { z } \left[ z _ { 2 } \right] = \mathbb { E } _ { \mathcal { T } } [ f ( \mathcal { T } ( x ) ) ]$

前面的一次step近似推导可以省略掉期望E，但是由于predictor h的存在，可以不进行一次step近似，predictor h可以弥补 $z _ { 1 }$ 和期望E的gap。实际上，直接计算出数据增强 $\mathcal { T }$ 的期望E是不现实的，但是可能直接通过predictor h来预测出期望E(因为多个epoch中数据增强 $\mathcal { T }$ 的采样是一个隐式分布，可以通过学习的方式记住)。

Symmetrization

上述推导没有考虑对称计算loss的情况，实际上，对称loss相当于一次SGD密集采样数据增强 $\mathcal { T }$ ，也就是优化效率高一倍。

上述实验验证了这个结论，对称loss优化效率大大提高，非对称loss即使使用两倍训练时间，效果也不如单倍对称loss，猜测因为对称loss下数据量更多，从k-means的角度考虑聚类效果会更好。

EMA

SimSiam进一步发现predictor h用来预测期望E不是必须的，还有其他的替代方案。SimSiam又做了一个对比实验，去掉predictor h的SimSiam其实就是上面推导的一次step近似，使用momentum encoder(EMA)来得到 $\eta _ { x }$ ，EMA相当于提供了更多数据增强 $\mathcal { T }$ 的views的近似期望E，在没有predictor h的时取得55.0%的精度；但是如果同时没有EMA和predictor，精度迅速掉到0.1%。这两个实验侧面证实了EMA和predictor都能起到预测期望E的作用。

并且EMA和predictor的实验同时说明了SimSiam和BYOL没有负样本对也能work的原因，因为SimSiam虽然没有EMA但是有predictor，BYOL既有predictor也有EMA。

总结

SimSiam的理论解释意味着所有带stop-gradient的孪生网络表征学习都可以用EM算法解释。stop-gradient起到至关重要的作用，并且需要一个预测期望E的方法进行辅助使用。但是SimSiam仍然无法解释模型坍塌现象，SimSiam以及它的变体不坍塌现象仍然是一个经验性的观察，模型坍塌仍然需要后续的工作进一步讨论。

看懂了SimSiam对孪生网络表征学习的解释，再看其他应用孪生网络的算法就清爽了许多，SimSiam值一个best paper(虽然只拿了2021 CVPR Best Paper Honorable Mention)。

Reference

[1] Exploring Simple Siamese Representation Learning

[2] https://zhuanlan.zhihu.com/p/36331115

[3] https://zhuanlan.zhihu.com/p/367290573


往期精彩回顾




适合初学者入门人工智能的路线及资料下载
机器学习及深度学习笔记等资料打印
机器学习在线手册
深度学习笔记专辑
《统计学习方法》的代码复现专辑
AI基础下载
黄海广老师《机器学习课程》视频课
黄海广老师《机器学习课程》711页完整版课件
本站qq群955171419，加入微信群请扫码：