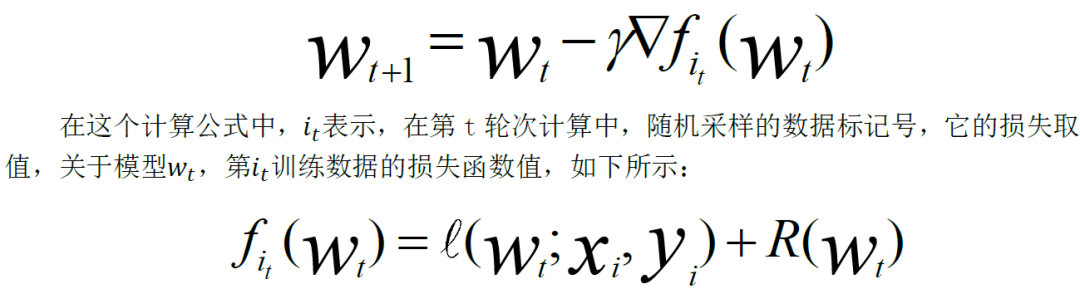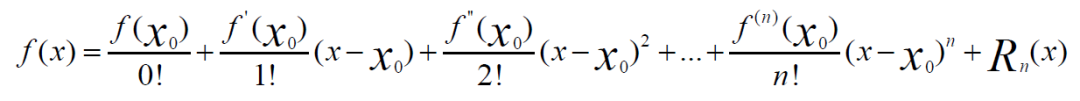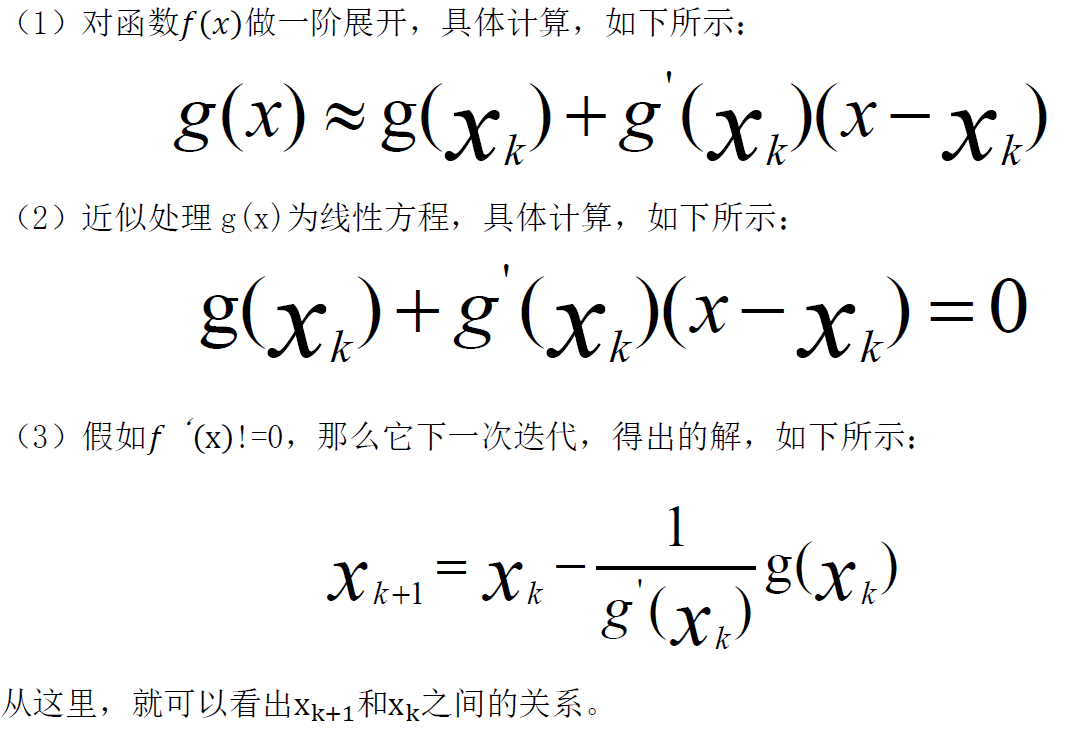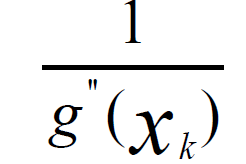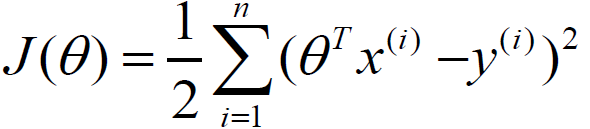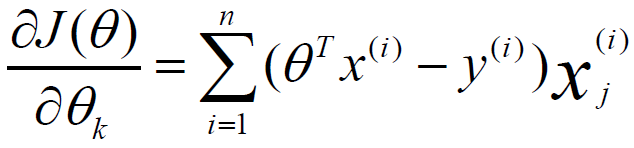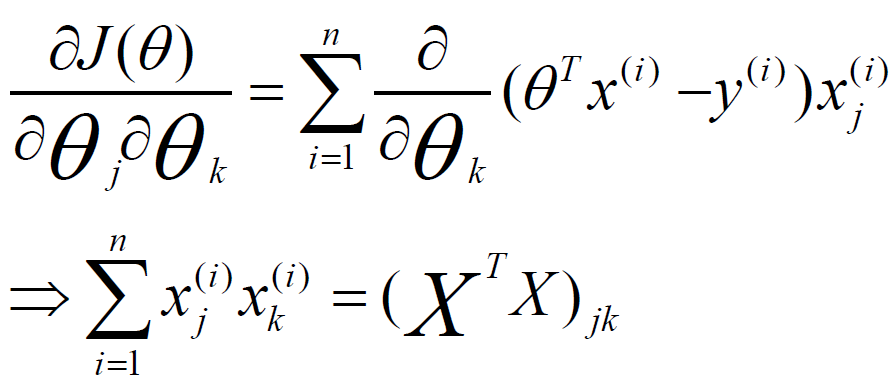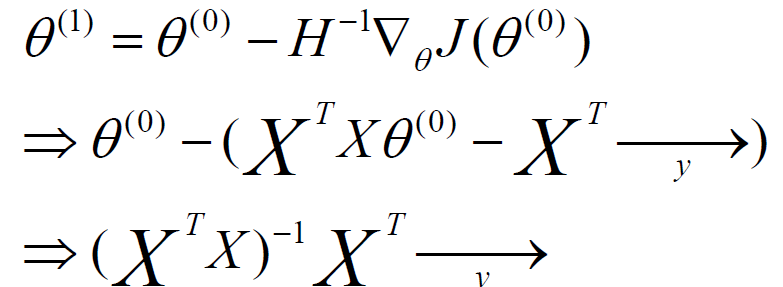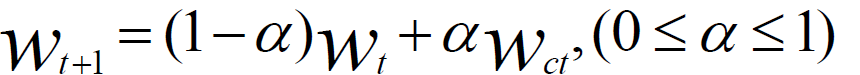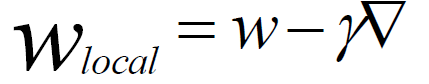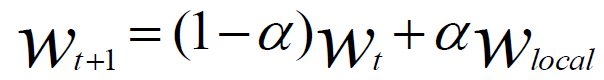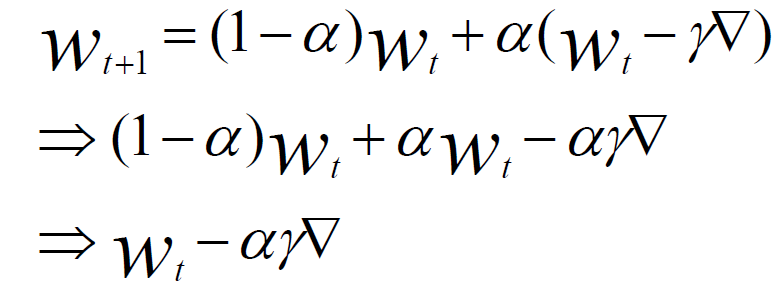在分布式算法改进后,算法因为分布式情况,存在通信、等待、同步、异步等问题,导致算法的空间复杂度、时间复杂度,没有达到预想的情况,针对机器学习的单体算法和分布式算法的优化方法,本节就来介绍相关原理和实现方法一、单体算法优化
针对机器学习的算法模块,我们需要将它定性成为不同的功能模块,对算法进行优化,并且拆解成为分布式的优化方法,本节先来探讨单体算法的优化方法。我们先从简单的线性规划进行处理,线性回归的目标函数,如下所示:
如果使用梯度下降法法,每次更新模型,会随着数据量和数据维度,计算量进行线性增加,我们需要采用一些方法,降低它的计算规模。最常用的单体优化算法,是随机梯度下降算法SGD。它采用对数据样本,进行随机采样,它的更新公式,如下所示: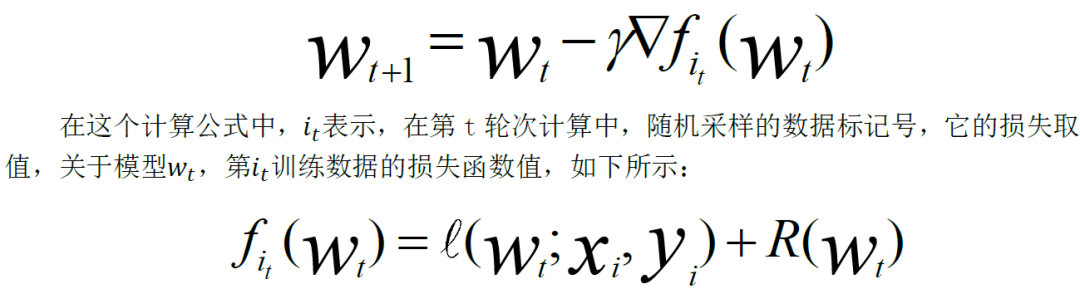
void Stochastic_gradient_descent(){ initialize:初始化w0参数 Iterate:for t= 0,1,…,T-1 遍历所有样本 Selecte:随机选取样本 计算:获得梯度 更新:更新参数}
对于全局的样本,都用来计算,会取得数据损失函数的平均值,我们采用随机更新,随机抽取样本,可以大大减少计算量,使用随机梯度作为梯度的自然替代,可以极大提高学习效率。除了随机梯度的方式,也可以使用随机坐标下降,对整体算法进行优化。它的原理是对模型维度进行随机采用,从而优化算法模型的训练,它的更新公式,如下所示:
void random_coordinate_descent(){ Initialize: 初始化w0参数 Iterate:for t= 0,1,…,T-1 遍历所有样本 Selecte:随机选取模型维度 计算:获得梯度 更新:更新参数}

牛顿法,也是一个高效的优化算法,它的核心是使用泰勒展开式,来实现优化,它的更新公式,如下所示: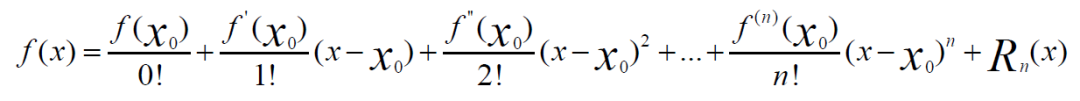
当我们使用一阶泰勒站开始,求取零点,计算方法如下所示:
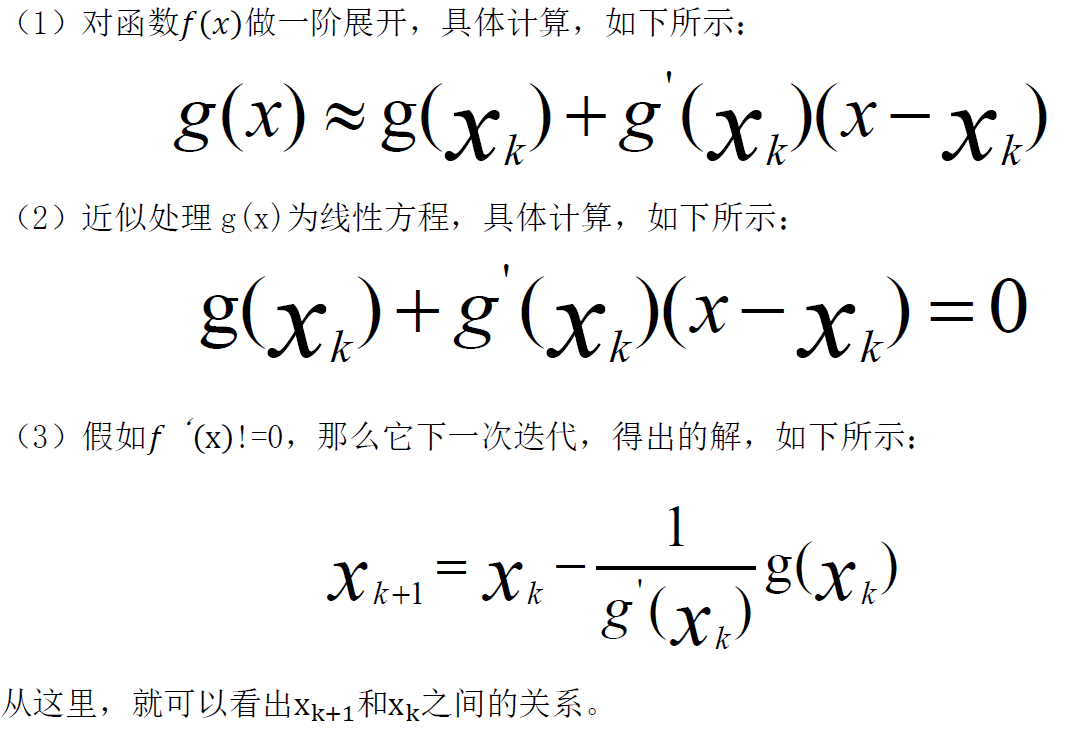

由此,我们可以看出最优化求解,最终迭代的形式,归纳方程,如下所示:
求解目标函数最小值,不断迭代,沿着函数下降方向,逐步到达最优店,牛顿法,每次迭代步长值,如下所示: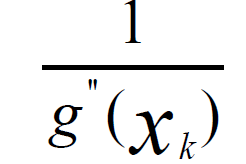
当我们在实际的模型优化应用中,可以先对损失函数,进行一阶、二阶求导,具体如下所示:
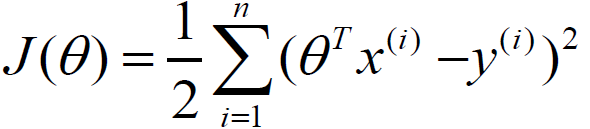
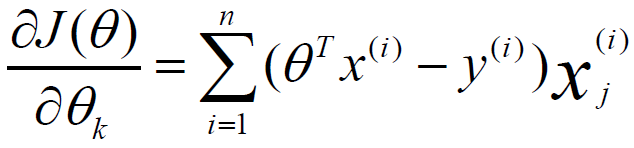
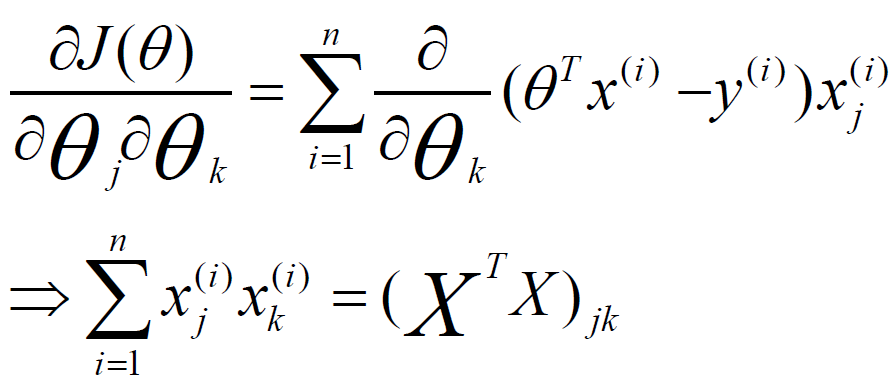
最终求和公式,转换为一个矩阵乘法的转换,参与1和参数0之间的关系,可以求解如下所示:
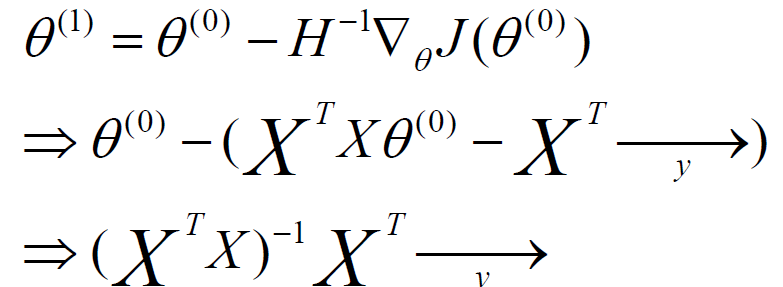
其中H就是二阶导数的简化,它被称为hessian矩阵,J函数表示对参数的一阶求导,大写的X和y表示矩阵,这就是牛顿法应用在最优参数求解的应用。
二、分布式异步随机梯度下降
在本书中,我们介绍了几个经典的单机优化算法,在分布式系统下,我们还可以借助分布式的计算能力,再次提高优化效率,本节应用随机梯度下降算法为例,讲解分布式的算法优化方法。假设我们有一个集群服务器,设置四个计算节点W1、W2、W3、W4,W1负责迭代两个模型参数a、d,W2负责迭代产生参数b、e,W3负责迭代产生参数c、f,W4作为最后的计算节点,产生参数g,把它们的参数传递顺序,以数字标注传递顺序。通过BSP协议,W1、W2、W3先将参数a、b、c传递给参数服务器,等待W4传递参数g给参数服务器,参数服务器根据获得的数据,计算平均真实梯度值,获得最新全局参数,同步全局参数到所有工作节点,计算节点W1、W2、W3获得参数,进入下次迭代,计算得到参数d、e、f。具体工作流程,如图1所示: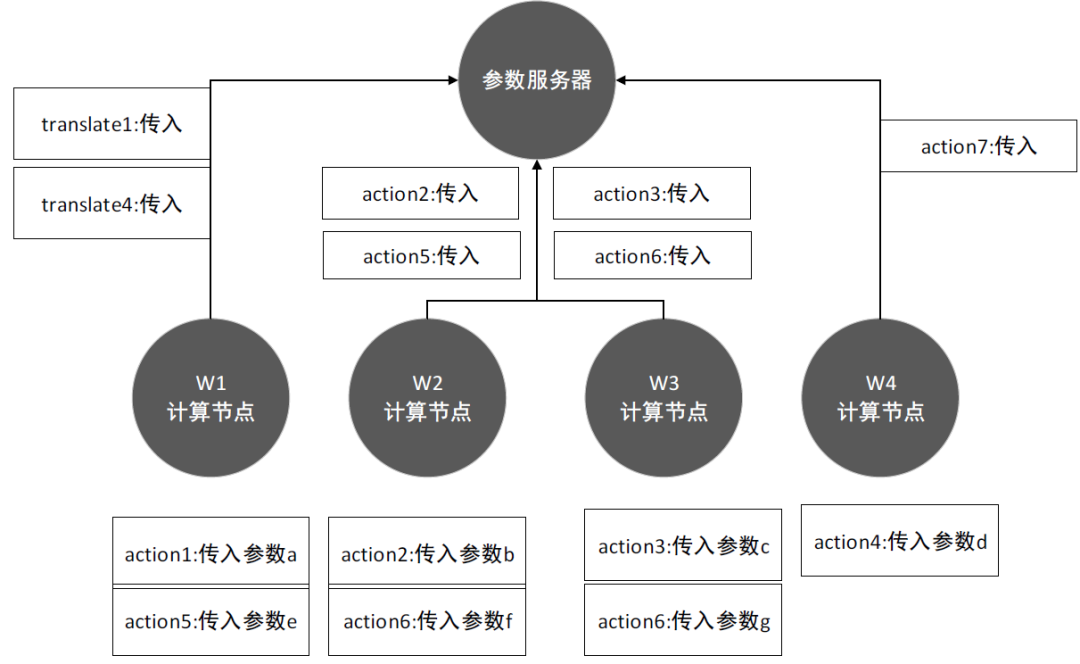
在异步更新的情况下,传递参数的顺序和上面相同,它不用进行等待,W1、W2、W3传递参数给参数服务器后,会立即获得更新后的全局参数,进入下次迭代,这样会导致产生多个全局参数的版本。在异步环境下,使用梯度值对全局进行更新,对于算法的收敛影响比较大,如图2所示,是异步参数的更新情况: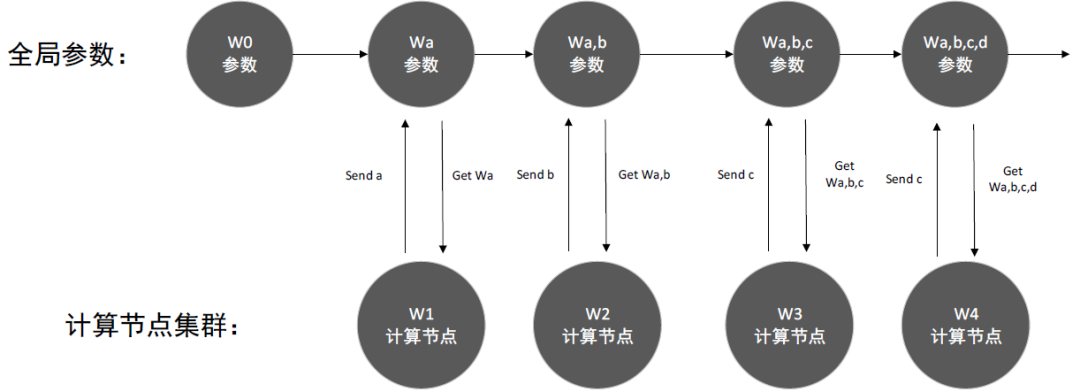
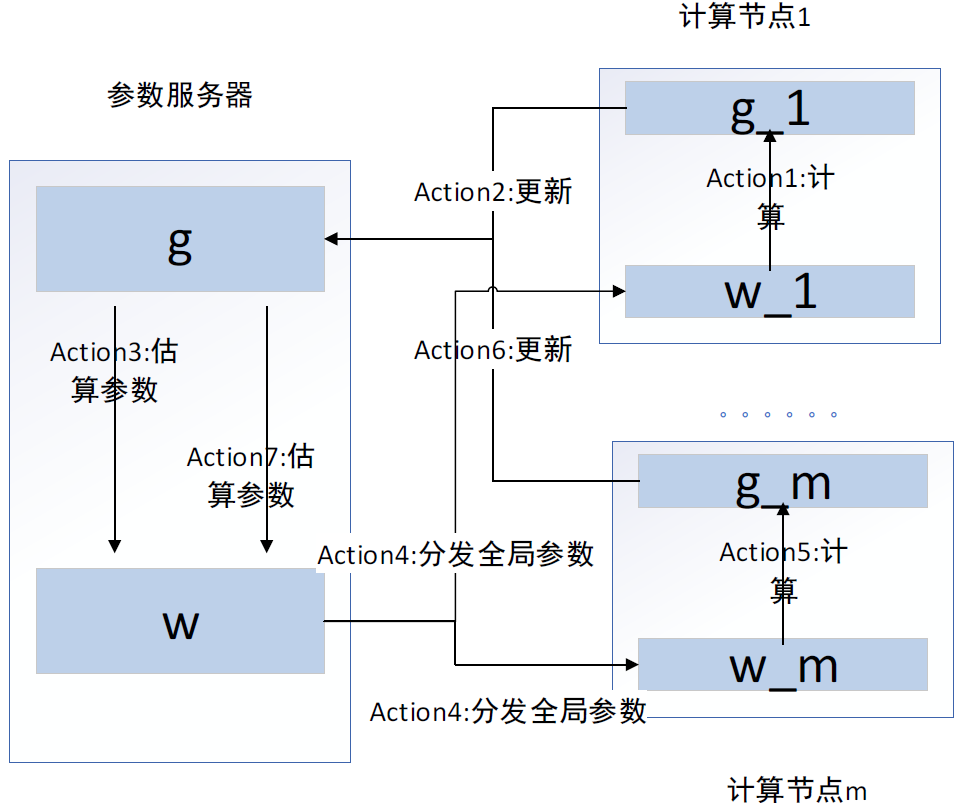
针对异步更新,残生多个全局参数,算法收敛的问题,我们可以进行如下处理:(1)在计算节点上,分别计算梯度值,不直接发送给参数服务器,使用梯度值,计算本地权重参数。(2)发送权重参数给参数服务器,参数服务器接收本地参数后,使用本地参数,更新全局参数。(3)使用Wt表示当前参数服务器的全局参数,Wct表示计算节点传的参数值,Wt+1表示计算后的新全局参数,再引入变量α,表示本地参数在全局权重,最终它的计算公式如下所示: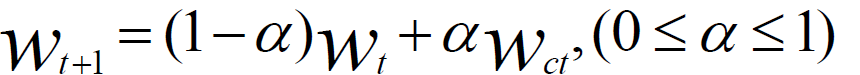
在工作节点更新是,不完全参数服务器上的参数,每个计算节点,智能代表它这个节点的结果,全局更新时候,需要根据所有工作节点的参数值和权重,进行根性,这里可以使用线性插值法,具体计算如下所示:
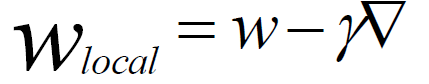
(2)参数服务器,接收到某个计算节点的参数,更新它的参数公式,如下所示:
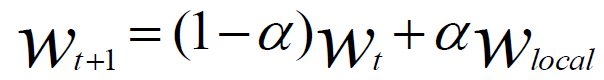
(3)合并上述两步,最终得到参数服务器参数,根据某个计算节点的权值参数,修正全局参数的公式,如下所示:
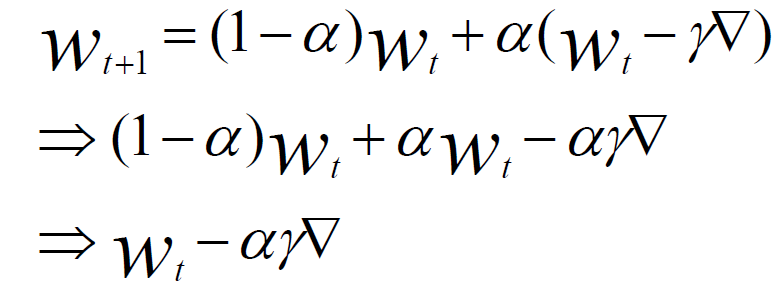
如果计算节点只有一个,和同步SGD算法的公式,也保持了一致。
void SGD_Client(){ ProcedureWork(Parameterw,Mini-batch-sizeNc Initialize:total gradientg = 0 For all i∈{1...Nc} do g←g + ComputeGradient(data,w) End For Server.Update(c,g) stepc ←stepc +1}
void SGD_Server(){ Procedure DispatchJob(Client c,Parameter wt) Call procedure Work(wt,Nc)for client c End Procedure Update(Client c,Gradient g) wt+1 ←wt − AdaGrad(g) t←t+1 If c is the last client whose stepc =the server step then step←step+1 End If If running then DispatchJob(c,wt) End If End}
以上我们就完成了随机梯度下降算法,在分布式异步环境的算法改进,关于其他的算法改进,读者可以参考上述原理,自行研究改进方法,适应应用环境。本书摘自机械工业出版社---《分布式人工智能:基于TensorFlow RTOS与群体智能体系》一书,经授权刊登此公号。

《分布式人工智能基于TensorFlow、RTOS与群体智能体系》结合分布式计算、大数据、机器学习、深度学习和强化学习等技术,以群体智能为主线,讲述分布式人工智能的原理与应用。本书首先介绍分布式系统的概念、技术概况、计算框架、智能核心及体系架构等内容;然后介绍大数据框架、高速计算、海量存储及人工智能经典算法等内容;接着介绍大规模分布式系统架构与演进,以及群体智能与博弈等内容;最后搭建《星际争霸2》仿真环境,并开发相关的仿真对抗系统。

如果你对以上内容感兴趣
快在留言区大声告诉我们
截止2月1日晚八点
留言获赞数最高的五位同学各赠一本
《分布式人工智能基于TensorFlow、RTOS与群体智能体系》

没有抽中的粉丝不要气馁,可在当当网购买此书,快快来抢购吧。
上述内容,如有侵犯版权,请联系作者,会自行删文。