【CV】相对位姿估计的进展和新方法
审稿&修改：赵季博士
第三部分，赵博士介绍了从新的几何特征“射线－点－射线”中估计位姿。第四部分，赵博士介绍了N点法的全局最优位姿估计。
位姿估计背景介绍和经典方法介绍
位姿估计是三维视觉的重要基础，有着非常广泛的应用，例如无人机定位，无人车定位，三维重建等。
按照给定的观测不同，位姿估计可以分为三大类。根据点云求位姿，属于3D-3D位姿估计，称作点云配准问题，代表算法包括ICP，NDT，LOAM等。根据图像点和地图点求位姿，属于3D-２D位姿估计，称作绝对位姿估计，代表算法包括P3P，PnP等。根据具有公共视野的图像求位姿，属于2D-2D位姿估计，称作相对位姿估计，代表算法包括5点法、8点法、单应矩阵法等。本公开课重点关注2D-2D相对位姿估计方法。
赵博士首先介绍了经典的最小配置问题以及其最小配置解，即至少需要多少个点（观测）来求相对位姿。对于单目相机，最少需要5个点，对于多目相机或者广义相机，最少需要6个点。参考论文[C. Longuet-Higgins 1981], [D.Nister 2004], [H. Stewenius et al 05,06].
随后，赵博士介绍了定制化最小配置问题的三个研究方向，分别是：
1.利用先验降低问题的自由度，例如已知旋转角、已知旋转轴、平面运动约束、阿克曼运动模型等
2.将其他变量和位姿同时估计，例如相机焦距、主点、畸变参数等。
3.处理非标准的位姿估计问题，例如使用新型的特征匹配恢复位姿（仿射匹配，射线-点-射线匹配）、处理新型相机或场景等。
最小配置问题的核心是求解多项式方程组。接下来，赵博士介绍了多项式方程组求解的方法以及工具。常见方法包括closed-form solution, companion matrix, Sturm sequence, Gröbner basis (格罗布纳基), resultant method (结式法), Wu’s method (吴文俊方法), homotopy continuation (同伦连续)等。工具包括Macaulay2, Maple,以及方程求解器的自动生成程序。赵博士在公开课中着重介绍了针对多元高阶方程的Gröbner basis方法。Gröbner basis方法当前分为离线和在线两部分，离线构造出消元模板，在线填充消元模板中的非零元素，便于提高计算效率。感兴趣的同学可以看原公开课视频。
第一部分最后，赵博士介绍了最优位姿估计的研究方向，包括设计具有鲁棒性和全局最优性的算法，解的最优性认证，从两视图的位姿估计扩展到多视图，基于机器学习的位姿估计方法等。
5点法 & 6点法
赵博士在第二部分中介绍了他和合作者的工作，主要是对经典最小配置问题提出新的解法。在最小配置问题中，对于单目相机，最少需要5个点可以恢复位姿。而对于一般的多目相机，最少需要6个点。
（图1）左：单目相机 右：多目相机
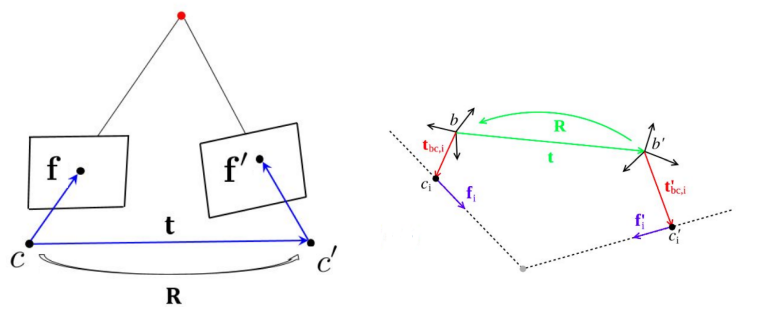
单目相机和多目相机的位姿恢复都可以根据方向向量和平移的共面性建立几何约束。
（1）单目相机
对于单目相机，经典的对极几何刻画了两个方向向量、平移向量t之间的共面关系。具体做法是建立约束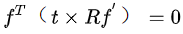
，即
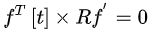，令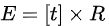
，称为本质矩阵，则
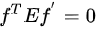。也可以不引入本质矩阵，使用更加直接的方式建模。例如，在[Kneip et al 2012 ECCV]中潜在地使用了一种表示形式：
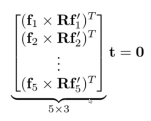
此时可以去掉t，令矩阵不满秩即可，任取矩阵3行构造的行列式应为0。这样就得到了只与R相关的约束，实现了R和t的解耦。当R求出后，对相应的5*3矩阵做SVD分解求t。
（2）多目相机
对于多目相机，不同相机的光心之间还有一个相对偏置，因此多目相机的对极几何变得复杂，为：
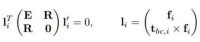
可以看出，单目情况的3维方向向量变成了6维的普吕克直线表示，单目情况的3*3的本质矩阵变成了6*6的广义本质矩阵。单目的五点法[D. Nister 2004]没法推广到多目情况。为了解决这个问题，[Stewenius, Astrom, Nister 2005]提出了一种匹配点深度参数化的解法，成为多年来几乎唯一的解法。
我们的旋转-平移解耦方法可以轻易地推广到多目相机。区别在于单目的5*3矩阵变成了6*4矩阵，再任取其中的4*4矩阵，令它门的行列式为0。此外，如果存在三个匹配在两个视图中都被相同的单相机成像，则需要增加3*3子矩阵的行列式为0的约束。
需要对旋转R给出合适的参数化方法，用于构建多项式方程。R有多种表示方法，赵博士列举了Cayley，Quaternion，Direction cosine matrix（DCM）三种方法。
如何去选择旋转的表示方法呢？好的表示方法要使方程组的阶次尽量低，未知变量尽量少，对称性尽量少。
赵博士工作用Cayley和quaternion表示方法来求解5点法[1]和6点法[3]中旋转矩阵R。Cayley表示旋转的具体5点/6点法求解步骤在视频中有讲解，感兴趣的同学请看原公开课，在此不赘述。
赵博士总结了R和ｔ解耦方法的一般步骤［３］：
1. 用R和t写出约束，R建议用Cayley或quaternion表示。
2. 将约束表示为M*t=0，其中M只和R相关。单相机的t是3维，多相机系统的t是4维齐次坐标。
3. 让M子矩阵的行列式为0，构造多项式方程。
4. 对于多相机，如果存在三个匹配在两个视图中都被相同的单相机成像，则需要增加3*3子矩阵的行列式为0的约束。
5. 对于步骤3和4的多项式方程，除以Cayley或quaternion相关的尺度因子。
6. 使用多项式方程求解的工具链求出R，再求出t。
本部分最后，赵博士介绍了其工作的实验结果。5点法对纯旋转比较友好，扩展性强。6点法相比于之前方法具有更高的效率，更好的数值稳定性，扩展性更强，可以方便地推广到各种复杂的定制化问题。
从射线－点－射线(RPR)中恢复位姿
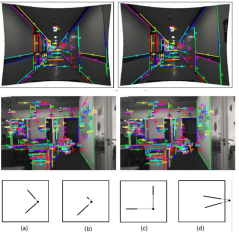
（图2）室内RPR几何结构
结构化环境中建图和定位时，注意到室内有很多线段结构。但是，理论上可以证明无法从两视图的线段匹配中恢复位姿。因此，提出了将射线-点-射线组成角进行匹配，这种结构称为RPR (ray-point-ray)。如果知道这种角结构在3D空间中的真实角度，我们就可以建立约束来估计位姿。如图三所示，为角结构的几何约束示意图。
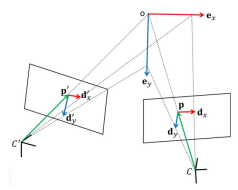
（图3） 二视图中的RPR约束
每个ray的观测引入了一个平面，可以求出平面的法向量。由于3D空间中的ray同时位于两个平面上，它的方向向量正比于两个法向量的叉乘。因此我们可以建立约束。
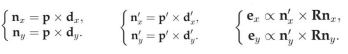
对于90度角：
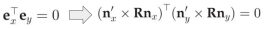
对于一般角：
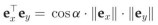
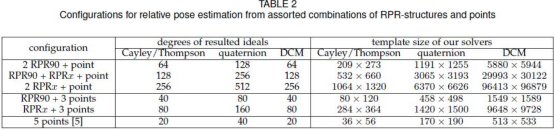
赵博士的实验结果如下。其中消元模板的尺寸是求解效率相关的指标，模板尺寸越小越好。可以看出，Cayley表示的求解效率是最高的。这种RPR约束具有理论价值，也为结构化场景的视觉定位提供了新思路。
N点法的全局最优位姿估计
第四部分中，赵博士介绍了用多点法求全局最优位姿。在实际工作中，冗余观测较多，而且存在噪声。因此，多点法相比于最小配置解法，具有更高的精度。
赵博士首先介绍了一些经典工作和相关论文。
1.代数误差
·LMI optimization [Chesi 2009 PAMI]
·local optimization, BnB [Kneip & Lynen 2013 ICCV]
·SDP + R-T representation [Briales et al 2018 CVPR]
2.几何误差（例如重投影误差）
·Gauss-Newton, Levenberg-Marquardt.
3.DLT method
·8 point method + normalization [Hartley 1997 PAMI]
4.Certifiable solvers for related tasks
·geometric perception [H. Yang & Luca Carlone ICCV’19, RAL’20, CVPR’20, NIPS’20]
·certifiable solvers [Briales et al IROS’16, ICRA’17, CVPR’17, Garcia-Salguero et al IVC’21]
·rotation averaging [Rosen et al IJRR’19, Eriksson et al CVPR’18, Dellaert et al ECCV’20]
然后赵博士介绍了通过几何约束建立约束模型、和最小配置解不同的是，多点法需要考虑噪声，因此从解方程问题变成了优化问题，优化目标是使方程的残差尽可能接近0。
使用代数误差时，优化问题为
其中，归一化本质矩阵的集合定义为：
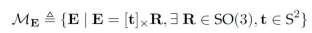
对目标函数进行整理，变为标准的二次型
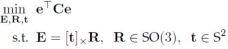
由于归一化本质矩阵的充分必要条件为
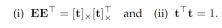
可以减少约束中的未知数，把问题重新整理为标准QCQP问题：
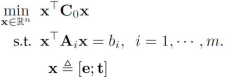
我们需要对上述优化问题进行求最优值，下图为非凸QCQP问题的求解框架。核心思想是把原来的非凸优化通过半正定松弛转化为凸优化。求解完毕后再将最优解返回到原问题。
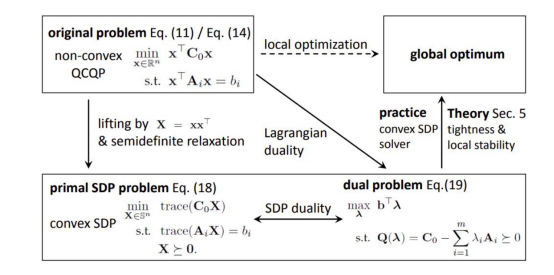
最后，赵博士介绍了一些相关的主题：
1. 松弛紧性（tightness）的判断、松弛的局部稳定性证明；
2. 把N点法嵌入到鲁棒框架，得到鲁棒N点法；
3. 实验结果，包括效率评估、鲁棒N点法的精度和鲁棒性、匹配点的个数与位姿精度的关系等。
Tutorial & Survey
1).The art of solving minimal problems
-http://cmp.felk.cvut.cz/minimal-iccv-2015/
-http://cmp.felk.cvut.cz/minimal-cvpr-2019/
2).Minimal Problems in Computer Vision
-http://aag.ciirc.cvut.cz/minimal/
6).Global Optimization for Geometric Understanding with Provable Guarantees
-https://mit-spark.github.io/GlobalOptimization-ICCV2019/
CAS Software
1).Macaulay2:
- http://www2.macaulay2.com/Macaulay2/
2).Maple software
Automatic solver generator程序
1).Automatic generator for minimal solvers.
- http://people.inf.ethz.ch/vlarsson/
2).Automatic generator.
- https://github.com/PavelTrutman/Automatic-Generator
3).Polyjam.
- https://github.com/laurentkneip/polyjam
4).Gaps.
- https://github.com/prclibo/gaps
教材
1).D.Cox et al. Ideals, Varieties, and Algorithms. Springer, 2013.
2).D.Cox et al. Using Algebraic Geometry. Springer, 2006.
中文资料
1).王东明, 等. 计算机代数(第二版), 清华大学出版社, 2007.
2).李超, 等. 计算机代数系统的数学原理. 清华大学出版社, 2010.
https://www.bilibili.com/video/BV1p7411c7mz?p=1
[1] Ji Zhao, Laurent Kneip, Yijia He, and Jiayi Ma. Minimal Case Relative Pose Computation using Ray-Point-Ray Features.
IEEE Transactions on Pattern Analysis and Machine Intelligence, 42(5): 1176 - 1190, 2020.
[2] Ji Zhao. An Efficient Solution to Non-Minimal Case Essential Matrix Estimation. IEEE Transactions on Pattern Analysis and Machine Intelligence. DOI: 10.1109/TPAMI.2020.3030161.
[3] Ji Zhao, and Banglei Guan. On Relative Pose Recovery for Multi-Camera Systems. ArXiv:2102.11996.
Webpage:
https://sites.google.com/site/drjizhao/
Github:
https://github.com/jizhaox
往期精彩回顾 本站qq群955171419，加入微信群请扫码：