Flood Fill 算法模型详解-技术圈

来源：小小算法

作者：小小算法

Flood Fill 算法模型详解

Flood Fill 在图像处理领域大显身手。例如 photoshop 的魔法棒，当我们点击图像上的一个像素点的时候，魔法棒就帮我们把和这个像素点颜色相近的周围像素点全都选取了，这就是 Flood Fill 算法的一个典型应用。

颜色自动填充

Flood Fill 的中文翻译是“漫水填充”。在这篇文章中，我们一起通过一道简单的算法题来揭开它的神秘面纱。

我选择的这道算法题是 leetcode 733 图像渲染[1]，它是 leetcode 的简单题，这篇文章的主要目的并不是讲解这道题，而是借助这道典型的 Flood Fill 题，我们一起来对这一类题型做一个总结，提取出它们的共同特征和解题思路。

题目描述

给你一个坐标 (sr, sc) 和一个新的颜色值 newColor，让你重新上色这幅图像。

上色规则是，从 (sr, sc) 开始，将与它颜色值相同的周围区域像素点的颜色值改为 newColor 。这里周围区域指的是，通过上下左右四个方向能够到达的区域，除非碰到与它颜色不一样的像素点。

例如：

输入: image = [[1,1,1],[1,1,0],[1,0,1]] sr = 1, sc = 1, newColor = 2

输出: [[2,2,2],[2,2,0],[2,0,1]]

我们分别使用 DFS 、 BFS 和并查集来分析这道题，Flood Fill 这类题都可以使用这三种算法来解决。

对 DFS 和 BFS 不熟的同学可以先看看我之前写过的文章：一题看透 DFS 和 BFS。

深度优先搜索

我们可以从开始位置(sr, sc)出发，依次向它的四个方向进行搜索，搜索之前要先把当前像素点的颜色改为newColor。

image[r][c] = newColor;
int vx[] = {0, 0, 1, -1};
int vy[] = {1, -1, 0, 0};
for (int i = 0; i < 4; i++) {
int newr = r + vy[i];
int newc = c + vx[i];
    dfs(image, newr, newc, newColor, color);
}

这样一直搜索下去肯定不行，要注意 DFS 的结束条件：

当位置（行或列）超过数组的边界时，要结束递归。

if (r >= image.size() || c >= image[0].size()) {
return;
}

如果当前位置的颜色值和开始位置(sr, sc)的颜色值不同时，我们不能修改它的颜色值，要结束递归。

if (image[r][c] != color) {
return;
}

还有一点要注意的是，当要修改的目标颜色值newColor和开始位置的颜色值image[sr, sc]相同时，我们不需要对image做任何改变，原image就是最终的image.

int color = image[sr][sc];
if (color == newColor) {
return image;
}

广度优先搜索

BFS 就是一层一层的往外边搜索边扩张，使用队列来实现。

一开始我们先把开始位置(sr, sc)加入队列，并且修改它的颜色值：

queue<vector<int>> q;
q.push({sr, sc});
image[sr][sc] = newColor;

然后队首元素出队列，同时把它上下左右四个方向颜色值为color的位置加入到队尾，并修改它们的颜色值为newColor。重复操作，直到队列为空。

int vx[] = {0, 0, 1, -1};
int vy[] = {1, -1, 0, 0};
while (!q.empty()) {
vector<int> pos = q.front();
    q.pop();
// 标注1
// image[pos[0]][pos[1]] = newColor;
for (int i = 0; i < 4; i++) {
int r = pos[0]+vy[i];
int c = pos[1]+vx[i];
if (r >= image.size() || c >= image[0].size()) {
continue;
        }
if (image[r][c] == color) {
// 标注2
            image[r][c] = newColor;
            q.push({r, c});
        }
    }
}

注意

这里特别要提醒的是，一定要在添加到队尾的同时修改颜色值，不要在出队列时再修改颜色值。 也就是说修改颜色的代码，要放在标注2处，不能放在标注1处。

解释

如果等到出队列时再修改颜色值，那对于已经添加到队列中的像素点，虽然他们已经在队列中，但颜色并未及时修改。如果此时出队列的像素点正好位于某个已经在队列中的像素点旁边，那这个已经在队列中的像素点，就会被重复添加到队尾了。

轻则导致耗时增加，严重的话会出现提交超时错误。

并查集

我们先来看一下 Flood Fill 的定义：漫水填充法是一种用特定的颜色填充连通区域，通过设置可连通像素的上下限以及连通方式来达到不同的填充效果的方法。

定义中多次提到连通，而并查集就是用来解决动态连通性问题的！

来源网络

假设开始位置(sr, sc)的颜色为color。我们可以使用并查集把颜色值为color并且位置相邻的像素点连通起来，形成一个连通集合。颜色值不是color的每个像素点，单独作为一个集合。

例如下面这种情况（圈起来的是开始位置），使用并查集就把它分成了 4 个连通集合。这时我们只需要把所有和开始位置(sr, sc)在同一个集合的像素点的颜色改为newColor就行了。

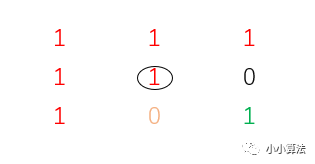
怎么把它们分成若干个集合呢？我们从(0, 0)位置开始依次遍历，这时就不需要同时兼顾上下左右四个方向了，只需要看看它右边和下面的像素点颜色是不是和我一样都为color，一样就合并。不一样就不管它，让它自己单独作为一个集合。

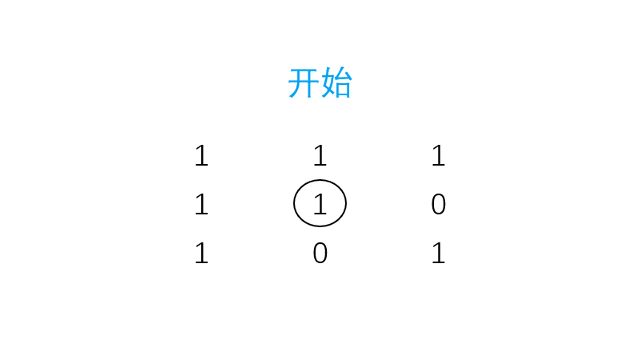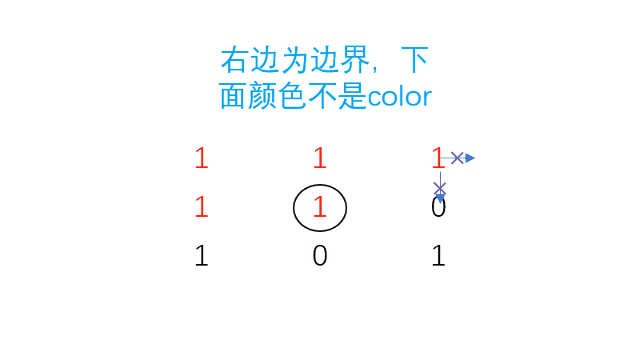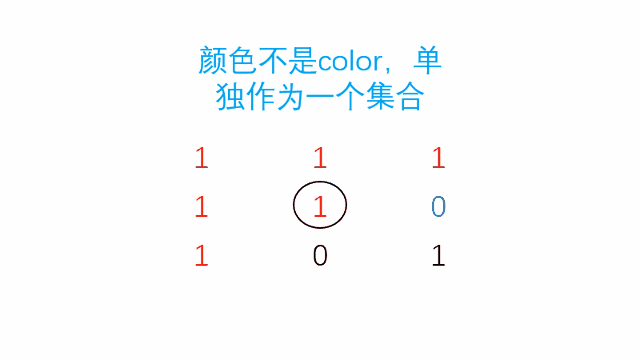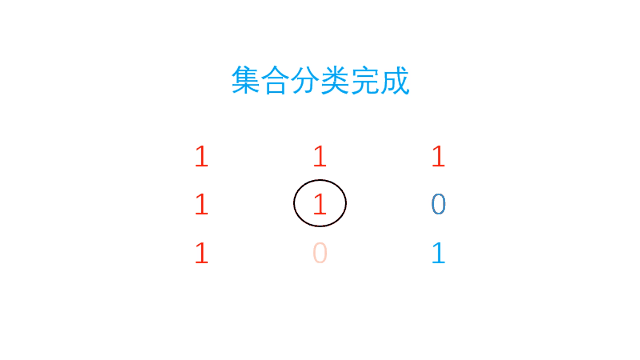动图演示

提示，这里每个像素点的位置是二维坐标(row, col)，为了方便我们需要将它们的位置映射为一维形式:row * colNum + col。row表示行坐标，col表示列坐标，colNum表示数组的列数。

for (int i = 0; i < rowNum; i++) {
for (int j = 0; j < colNum; j++) {
if (image[i][j] != color) {
continue;
        }
int right = j+1;
int down = i+1;
if (right < colNum && image[i][right] == color) {
            u.unio(i*colNum+j, i*colNum+right);
        }
if (down < rowNum && image[down][j] == color) {
            u.unio(i*colNum+j, (down)*colNum+j);
        }
    }
}

那么接下来我们就只需要把和开始位置(sr, sc)在同一个连通集合的像素点颜色值置为newColor就行了。

for (int i = 0; i < rowNum; i++) {
for (int j = 0; j < colNum; j++) {
if (u.connected(i*colNum+j, sr*colNum+sc)) {
            image[i][j] = newColor;
        }
    }
}

总结

通过上面这道题的分析，我们可以总结出漫水填充算法题型有着这样的特征：空间都是按区域划分的，并且每个区域中的元素都是相邻的。

为了扩大它的解题范围，我们可以再进一步抽象，把一个个区域抽象为一个个集合，集合中的元素都存在着某种逻辑上的连通性。最典型的就是547. 朋友圈[2]。

Flood Fill 这类题还有很多，例如：1020. 飞地的数量[3]、1254. 统计封闭岛屿的数目[4]、547. 朋友圈[5] . . .。如果使用DFS或BFS的话，解决它们的步骤无非就是遍历、标记加计数。如果抽象为集合的话，我们就可以使用并查集对它们进行集合划分，最后只需要对目标集合中的元素进行操作就可以了。

好了，这就是这篇文章的所有内容，希望对您有帮助！喜欢，别忘了点亮在看哦！

代码

深度优先搜素

class Solution {
public:
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int newColor) {
int color = image[sr][sc];
if (color == newColor) {
return image;
        }
        dfs(image, sr, sc, newColor, color);
return image;
    }

void dfs(vector<vector<int>>& image, int r, int c, int newColor, int color) {
if (r >= image.size() || c >= image[0].size()) {
return;
        }
if (image[r][c] != color) {
return;
        }
        image[r][c] = newColor;
int vx[] = {0, 0, 1, -1};
int vy[] = {1, -1, 0, 0};
for (int i = 0; i < 4; i++) {
int newr = r + vy[i];
int newc = c + vx[i];
            dfs(image, newr, newc, newColor, color);
        }
    }

};

广度优先搜素

class Solution {
public:
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int newColor) {
int color = image[sr][sc];
if (color == newColor) {
return image;
        }
queue<vector<int>> q;
        q.push({sr, sc});
        image[sr][sc] = newColor;
int vx[] = {0, 0, 1, -1};
int vy[] = {1, -1, 0, 0};
while (!q.empty()) {
vector<int> pos = q.front();
            q.pop();
for (int i = 0; i < 4; i++) {
int r = pos[0]+vy[i];
int c = pos[1]+vx[i];
if (r >= image.size() || c >= image[0].size()) {
continue;
                }
if (image[r][c] == color) {
                    image[r][c] = newColor;
                    q.push({r, c});
                }
            }
        }
return image;
    }
};

并查集

class UnionFind {
private:
int* parent;

public:
    UnionFind(){}
    UnionFind(int n) {
        parent = new int[n];
for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }
int find(int x) {
while (x != parent[x]) {
            parent[x] = parent[parent[x]];
            x = parent[x];
        }
return x;
    }
void unio(int x, int y) {
        x = find(x);
        y = find(y);
if (x == y) {
return;
        }
        parent[y] = x;
    }

bool connected(int x, int y) {
return find(x) == find(y);
    }
};

class Solution {
public:
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int newColor) {
int color = image[sr][sc];
if (color == newColor) {
return image;
        }
int rowNum = image.size();
int colNum = image[0].size();
UnionFind u(rowNum * colNum);
for (int i = 0; i < rowNum; i++) {
for (int j = 0; j < colNum; j++) {
if (image[i][j] != color) {
continue;
                }
int right = j+1;
int down = i+1;
if (right < colNum && image[i][right] == color) {
                    u.unio(i*colNum+j, i*colNum+right);
                }
if (down < rowNum && image[down][j] == color) {
                    u.unio(i*colNum+j, (down)*colNum+j);
                }
            }
        }
for (int i = 0; i < rowNum; i++) {
for (int j = 0; j < colNum; j++) {
if (u.connected(i*colNum+j, sr*colNum+sc)) {
                    image[i][j] = newColor;
                }
            }
        }
return image;
    }
};