一网打尽!深度学习常见问题!

1  前言

在传统软件工程中，程序问题（即Bugs）会导致程序崩溃，但开发人员可以通过检查错误来了解原因。 然而，在深度学习中，代码可能会在没有明确原因的情况下崩溃。虽然这些问题可以手动调试，但深度学习模型通常会因为输出预测不佳而失败。更糟糕的是，当模型性能较低时，通常没有任何信号表明模型失败的原因或时间。 开发过程中我们很经常要花80-90%的时间在数据处理及调试模型，而只花费10-20%的时间推导数学方程和实现功能。 2  为什么模型的问题排查困难

• 很难判断是否有错误

• 造成相同性能下降的原因有很多

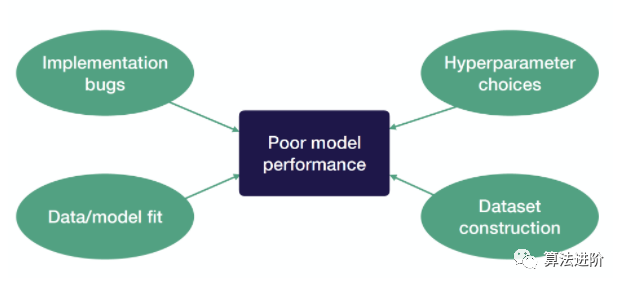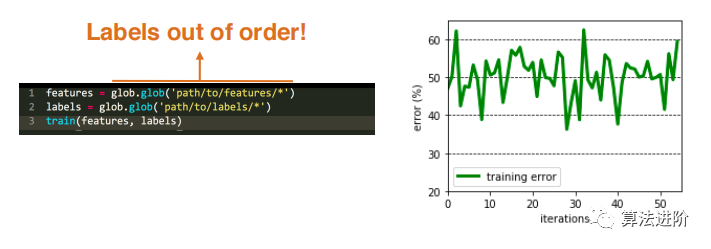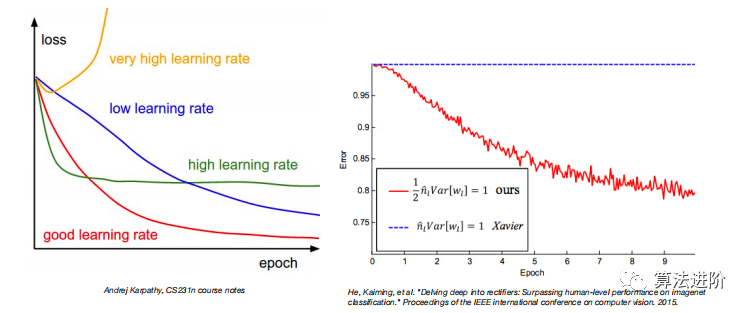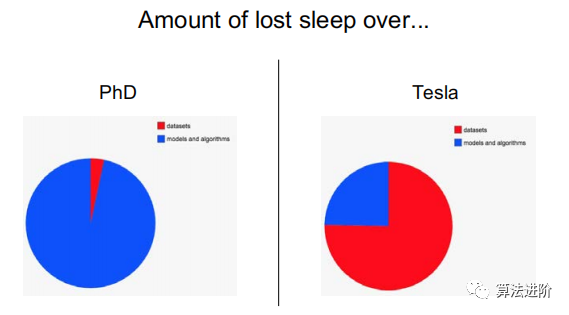• 结果可能对超参数和数据集构成的微小变化很敏感 2.1  存在隐藏bugs 在深度学习中，大部分错误并不会被轻易察觉到，比如标签顺序错误。 2.2  超参数选择 深度学习模型对超参数的选择非常敏感。即使是微妙的调整，如学习率和权重的初始化，也会对结果产生显著的影响。 2.3  数据/模型拟合 我们可以在ImageNet数据集上预训练模型，然后将其应用到更为复杂的自动驾驶汽车图像数据集上进行拟合。 2.4  数据集构造 在此过程中，常见的问题包括：样本数量不足、处理带有噪声的标签和类别不平衡、以及在构建训练集和测试集时未能确保数据的分布一致性。 3 深度学习故障排除指南 深度学习（DL）故障排除的关键思想：由于很难定位bugs的来源，因此最好从简单开始，逐渐增加复杂性。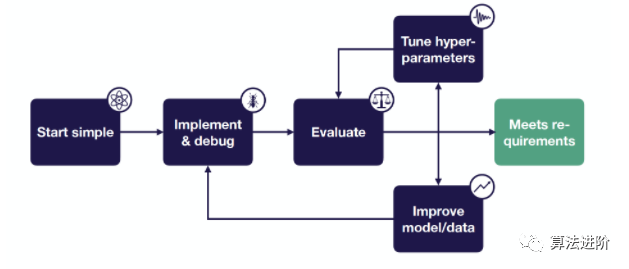 3.1  从简单开始 架构选择。 深度学习架构选择可遵循简单规则：图像数据，从类似LeNet开始，成熟时考虑ResNet；序列数据，从LSTM开始，问题成熟时转向注意力模型或WaveNet；其他任务，从全连接神经网络开始，再根据问题使用更高级网络。 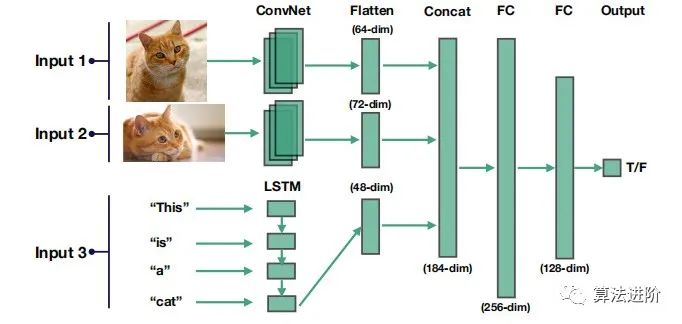使用合理的超参数默认值。 推荐的网络/优化器默认值： Adam 优化器使用 3e-4 学习率； ReLU 激活用于全连接和卷积模型以及 Tanh 激活用于 LSTM 模型；ReLU 激活函数采用 He 初始化，Tanh 激活函数采用 Glorot 初始化；模型未使用正则化或数据标准化。 归一化输入。 对输入数据进行归一化，减去均值并除以方差；对于图像，将值缩放为 [0, 1] 或 [-0.5, 0.5]（例如除以 255）。 简化问题。 使用小型训练集（约10,000个示例），固定对象、类、输入大小等，构建简单的综合训练集，可以提高模型解决问题的信心和迭代速度。 3.2  运行和调试 五个最常见的DL错误：

• 网络张量的形状不正确：可以无声地失败。例如，无声广播， x.shape = (None,), y.shape = (None, 1), (x+y).shape = (None, None)

• 错误地预处理输入：例如，忘记进行规范化，或进行过多的预处理；

• 模型损失函数的输入不正确：例如，Softmax 输出用于预期对数的损失；

• 忘记正确设置网络的训练模式：例如，切换训练/评估模式或控制批次范数依赖；

• 数值不稳定-inf/NaN：通常源于使用exp、日志或div操作。

关于实施模型的一般建议：

• 轻量级实现。第1个版本尽可能少的新代码行，经验法则是少于200行，不包括测试基础组件或TensorFlow/PyTorch代码；

• 使用现成的组件。使用Keras等现成组件，避免手动计算，以减少数值不稳定问题；

• 稍后构建复杂的数据管道。从可以加载到内存中的数据集开始。

运行模型常见问题及原因：

• 形状不匹配/转换问题：在调试器中逐步完成模型创建和推理，检查张量的形状和数据类型是否正确。

• 内存不足问题：逐个缩减内存密集型操作。例如，如果在代码中的任何位置创建大型矩阵，可以减小其维度的大小或将批量大小减半。

• 其他问题：标准调试工具包（ Stack  Overflow + interactive debugger）

过度拟合单批数据常见问题及原因：

• 误差上升： 可能是由损失函数/梯度中的符号翻转引起的、学习率过高、softmax使用了错误的维度；
• 误差爆炸：数值问题，检查所有的exp、日志和div操作、学习率过高；
• 误差振荡：数据或标签有误（例如，归零或错误打乱）、学习率过高；
• 误差不动：学习率过低、梯度没有在整个模型传播、过分正则化、损失函数的输入错误、数据或者标签有误。

与已知结果进行比较（不断迭代，直到模型执行得达到预期为止）：

• 在相似数据集上评估的官方模型实施；

• 根据基准评估官方模型实施（例如 MNIST）；

• 非官方模型实施；

• 论文结果（无代码）；

• 基准数据集（例如 MNIST）上的模型结果；

• 类似数据集上的类似模型的结果；

• 超级简单的基线（例如，输出平均值或线性回归）。 3.3  评估 偏差-方差分解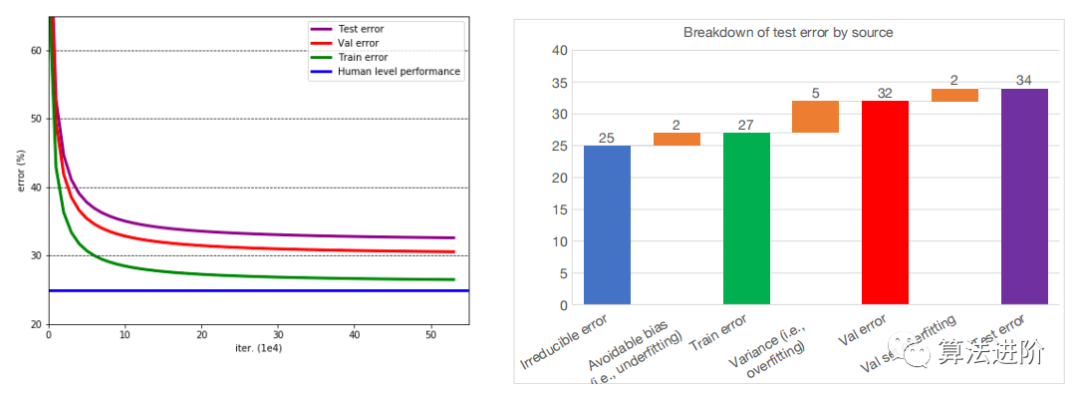 测试误差 = 不可约误差 + 偏差 + 方差 + 验证集过拟合 不可约误差是基线误差，可通过强有力的基线来估计。可避免偏差是欠拟合的衡量标准，是训练误差与不可约误差之间的差异。方差是过拟合的度量，是验证错误和训练错误之间的差值。验证集过拟合是测试误差与验证错误之间的差异。 随分布变化的偏差-方差 在实际的ML应用中，训练、验证和测试样本可能来自不同的分布。为了解决这个问题，可以创建两个验证集，分别来自训练分布和测试分布。通过比较测试验证错误和测试错误，可以估计分布偏移，这对于ML实际应用非常有用。 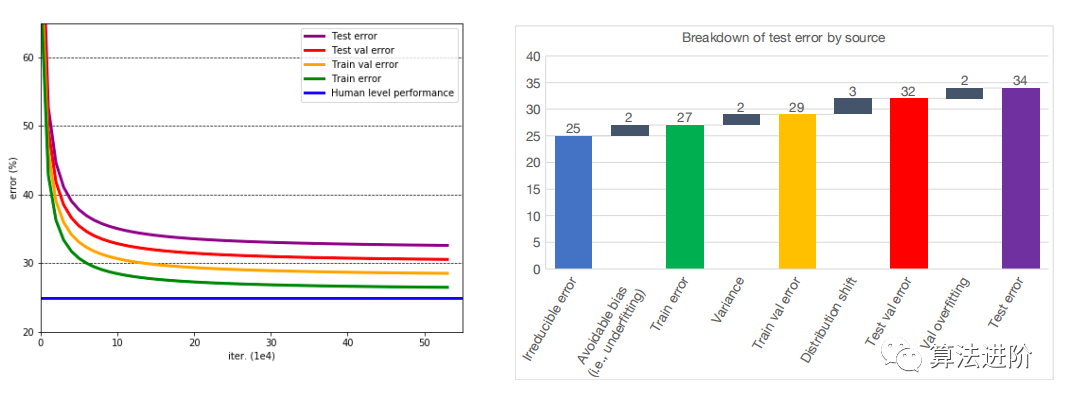测试误差 = 不可约误差 + 偏差 + 方差 + 分布偏移 + 验证集过拟合 3.4  改进模型和数据 解决欠拟合问题（即减少偏差）：优先级别递减

• 使模型更大（即添加层或每层使用更多单元）
• 减少正则化
• 误差分析
• 选择不同的（更接近最先进的）模型架构（例如，从 LeNet 迁移到 ResNet）
• 调整超参数（例如学习率）
• 添加特征

解决过拟合问题（即减少差异）：优先级别递减

• 添加更多训练数据（如果可能！）

• 添加归一化（例如批量归一化、层归一化）

• 添加数据增强

• 增加正则化（例如，dropout、L2、权重衰减）

• 误差分析

• 选择不同的（更接近最先进的）模型架构

• 调整超参数

• 提前停止（不推荐）

• 删除特征（不推荐）

• 减小模型尺寸（不推荐）

解决 分布转换

• 分析测试-验证集错误并收集更多训练数据进行补偿
• 分析测试-验证集错误并综合更多训练数据进行补偿
• 将领域适应技术应用于训练

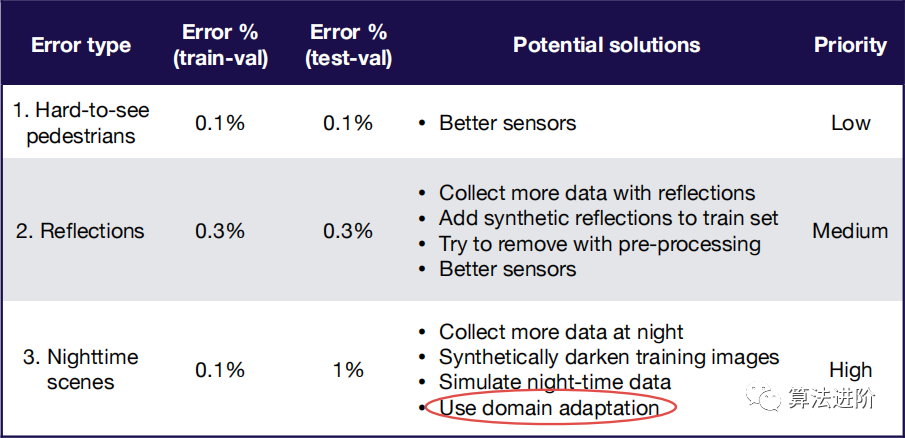误差分析示例如下： 领域适配 ：仅使用未标记数据或有限标记数据来训练“源”分布并推广到另一个“目标”的技术。当对测试分发中的标记数据的访问受到限制及可以获得大量相对相似的数据时要考虑领域适配。包括自监督领域适配和无监督领域适配。

重新 平衡数据集

• 如果 (test)-val 看起来明显比 test 好，则说明验证集过度拟合

• 这种情况发生在小验证集或大量超参数调整时

• 当它发生时，重新收集验证集数据

3.5  超参数优化 超参数优化面临如下问题：

网络：ResNet——多少层？如何参数初始化？卷积核大小？

优化器：Adam——batch size？学习率？beta1，beta 2？

正则化：用哪种正则化方式？

应该调整哪些超参数 ？ 首选 模型更敏感的参数；与选择的模型相关；经验法则；灵敏度与默认值相关。 有关超参数及其对模型的影响如下：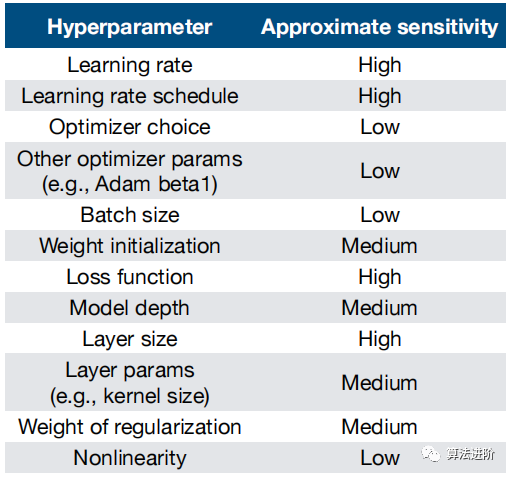

方法1  手动超参数优化

步骤： 了解算法（例如，更高的学习率意味着更快、更不稳定的训练）；训练和评估模型；猜测更好的超参数值并重新评估；可以与其他方法结合使用（例如，手动选择要优化的参数范围）。 优点： 对于经验丰富的人，只需要最少的计算就能获得良好的结果。 缺点： 需要对算法有深刻的见解且费时。

方法2  网格搜索

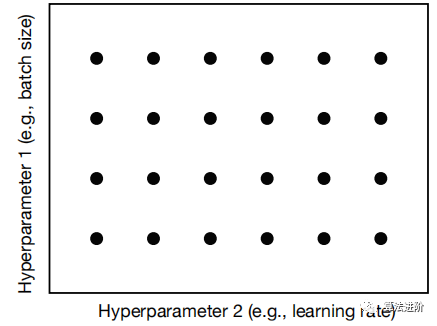优点： 实施起来超级简单；可以产生好的效果 缺点： 效率不高（需要对超参数的所有交叉组合进行训练）； 可能需要有关参数的先验知识才能获得良好的结果

方法3  随机搜索

优点：易于实施；通常会产生比网格搜索更好的结果

缺点：不太好解释；可能需要有关参数的先验知识才能获得良好的结果

方法4  由粗到细搜索

步骤： 定义一个大范围进行随机搜索，然后在结果池中找到N个最佳结果，并重复这个过程。 优点：可以缩小性能非常高的超参数范围；实践中最常用的方法 缺点：有点手动过程

方法5  贝叶斯超参数优化

步骤： 从参数分布的预先估计开始；维护超参数值与模型性能之间关系的概率模型；交替 使用最大化预期改进的超参数值进行训练并 根据训练结果来更新概率模型。 优点： 选择超参数最有效的  hands-of 方式。 缺点： 很难从头开始实施；可能很难与现成的工具集成。 总之，超参数方面应该从粗到细的随机搜索，随着项目代码完备后，再考虑贝叶斯等方法做更细致的超参数优化。

更多精彩内容请点击：AI领域文章精选！