笛卡尔坐标系这么简单,为什么姗姗来迟?
说起笛卡尔坐标系,可能会让你回想起中学里学习解析几何的美(tong)好(ku)时光。但不管怎样,应该都还记的平面直角坐标系以及空间直角坐标系。
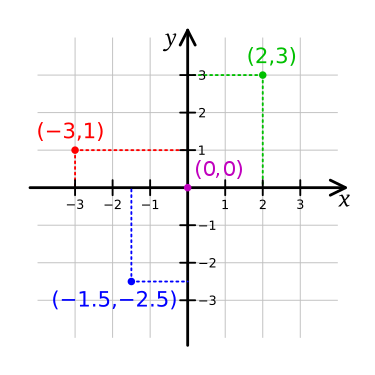

如果你进一步了解过,会发现笛卡尔坐标系可以包括笛卡尔直角(rectangular)坐标系以及笛卡尔斜角(oblique)坐标系。
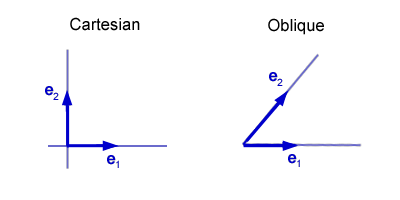
上图左边的直角坐标系貌似性质更好,它应该是首先被引入的,而右边的斜角坐标系可以看作直角坐标系的推广。但事实是否如此呢?
另外,坐标系并不复杂,聪明睿智的古希腊人没有想到吗?为什么到了十七世纪才提出来呢?我们来简单地回顾一下历史。
笛卡尔坐标系的由来
笛卡尔(Cartesian)一词源自于建立解析几何的哲学家兼数学家笛卡尔(Descartes)。但是,翻开笛卡尔的《几何》,你会发现,貌似找不到直角坐标系、坐标系这些概念,甚至连坐标这个术语都没有啊。
1637 年笛卡尔发表了他的名著《方法论》,而《几何》只是该书的三个附录之一。(插播一下,这个年份有点面熟啊。同年,明朝牛人宋应星的著作《天工开物》初刊。)
荷兰数学家 Frans van Schooten 是推动笛卡尔几何传播的主要人物之一。1649 年,他和学生将笛卡尔的《几何》翻译成拉丁文,在平面上明确引入了一对轴的概念,而笛卡尔在著作中并没有明确指定
《几何》的拉丁译本对传播笛卡尔著作中的思想发挥了重要作用。大神如牛顿也正是从读过的笛卡尔的《几何》中选了两个中心问题,即求曲线的切线和求曲线下的面积,也就是所谓的微分和积分问题。对于这两个问题,莱布尼茨在前面一批数学家的基础上也独立提出了他的方法。这个方法的核心是所谓的特征三角形(characteristic triangle),特征三角形的三条边就是函数某点处的

而坐标(coordinate)这个词是莱布尼兹在 1693 年左右引入的。1715 年约翰在与莱布尼兹的通信中引入了现在通用的由三个坐标平面建立空间坐标系的方法。至于阿基米德早在古希腊就有了微积分的思想,已经会用这种思想计算一些图形的面积了,但毕竟没有坐标系嘛,没有得出一般化的理论。
笛卡尔坐标(Cartesian coordinates)这个概念就更晚了,大概是在 1844 年才开始使用的。
在笛卡尔的基础上,后人还发展了许多其他坐标系,例如牛顿使用了平面极坐标,欧拉将其推广到三维空间等。
笛卡尔提出坐标系的思想也有一个类似牛顿与苹果的故事,那就是大家听过的蜘蛛网的故事。这个典故与牛顿的苹果类似,只是八卦,为枯燥的数学理论增加了一些谈资。

另外,还有关于那条心形曲线的美丽爱情故事,但讲这个故事时给出的曲线往往是用极坐标来表示的,而笛卡尔应该是不知道这个曲线的。
笛卡尔几何
我们都听说过笛卡尔在《几何》这个著作中提出了解析几何。但是,有个插曲,在笛卡儿的《方法论》发表前,另一位法国数学家费马也已经完成了用代数方程研究几何曲线的大作《平面和立体轨迹引论》,据说早在 1629 年就完稿了,但到了 1679 年才发表。因此,早于牛顿和莱布尼兹的微积分创建之争,解析几何的开创优先权之争落到了这两个大师身上,但后人乐于称笛卡儿和费马同为解析几何之父。

但当我们翻开书,发现找不到笛卡尔坐标。事实上,我们没有看到从它的方程中绘制出任何新的曲线。笛卡尔允许什么样的曲线呢?不是我们可能认为的任何具有方程的曲线。他只允许通过某种机械设备根据特定规则绘制曲线这种方式来构建的曲线。总之,我们没有找到解析几何这个术语,只是一种处理旧问题的革命性的新方法。
虽然笛卡尔并没有明确提出坐标系这一概念,但是后人还是给他冠名了。我们不禁要问,为什么呢?
古希腊的成就及问题
笛卡尔的思想是横空出世的吗?当然不是的,跟他的后辈牛顿等人一样,也是站住巨人的肩膀上的。
近代数学的发展自然离不开古希腊人的贡献,他们虽然超级厉害,但也是有缺憾的。我们简单回顾下古希腊在数量运算上的遗留问题。在这之前先来看一下他们取得的与笛卡尔的研究有关的成就。
我们知道古希腊毕达哥拉斯学派由于不可公度性而拒绝无理数,欧多克斯引入了量,建立了比例理论,部分化解了这次危机。数也许还存在问题,但研究几何量是没有问题的。比如勾股定理,古希腊称为毕达哥拉斯定理,用现在的符号表示为,
我们说这是勾股数啊,他们看来,这可以不关数,而是看成几何问题。这里一个量对应某个线段的长度,而它的平方自然是指面积了。欧几里得的证明也是从面积着手,可以看下图,证明三个正方形中相同颜色的面积等同即可。
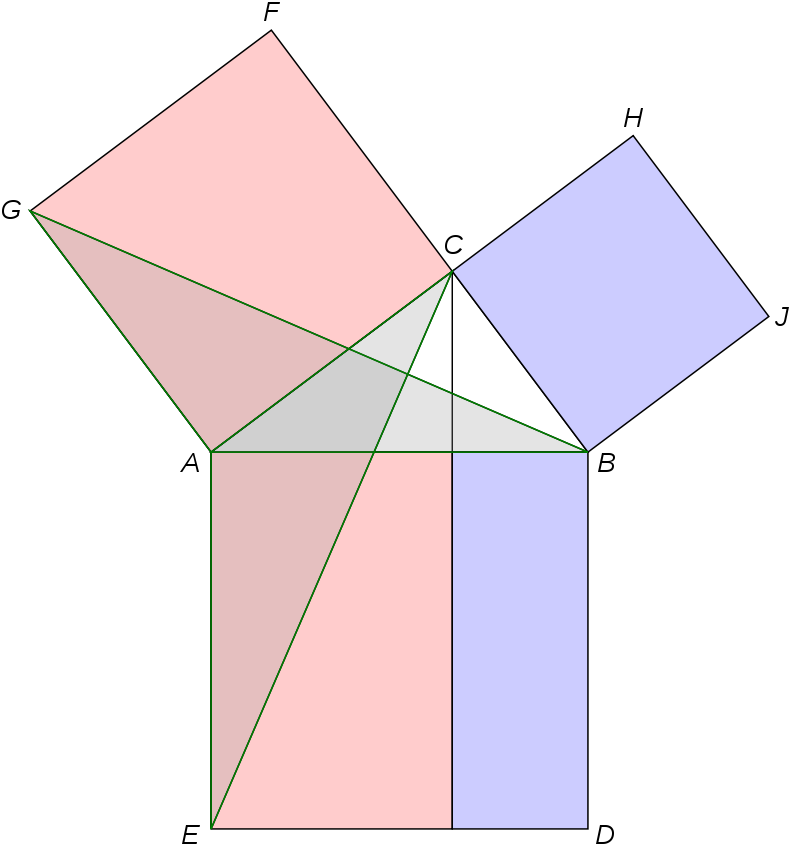
古希腊除了欧几里得,还有很多数学家值得提起,比如欧多克斯、梅内赫莫斯、阿基米德、阿波罗尼奥斯以及后期的代数学家丢番图等。
我们来看一下古希腊三大几何问题之一的倍立方体问题,用现在的符号来表达就是,给定
数学家希波克拉底(不是那个医生)表示,这个问题可以规约为在
然后,消掉
梅内赫莫斯在此基础上发现了另一个有趣的结论。如果我们只考虑公式的前两项,
可得
即
因此,倍立方体问题可以转化为找到抛物线和双曲线的交点的问题。其实还可以找出另一条曲线,用现在的坐标系来绘制这些曲线的话如下图所示。

正是这种归约促进了希腊人对圆锥曲线的研究兴趣。不过细细一想,这里貌似有个疑问。当初并没有坐标系啊,他怎么发现这些曲线的轨迹,还知道交于一点的呢?或者不妨假设他知道两个未知量的方程决定了一条曲线,并且已经引入坐标系来求解了,那岂不是已经建立解析几何了?
梅内赫莫斯也许使用了机械装置来绘制他的曲线。一般认为梅内赫莫斯使用平面切割圆锥的方法来研究圆锥曲线。阿波罗尼奥斯总结前人的成果,著有《圆锥曲线论》。
上过高中应该知道为什么叫圆锥曲线吧,我们来看一个动图回顾一下,
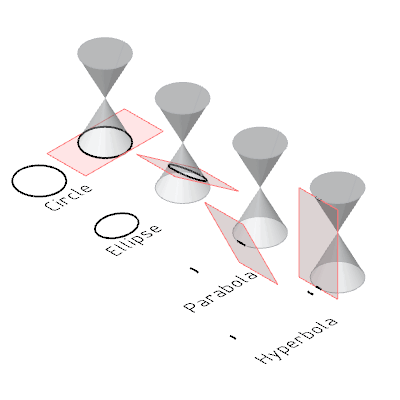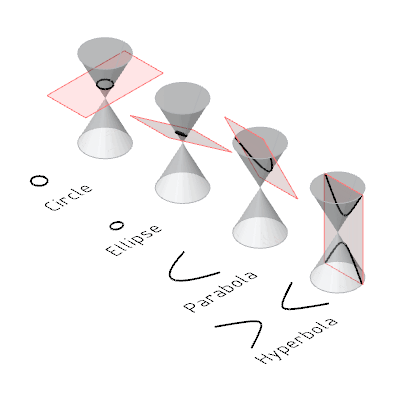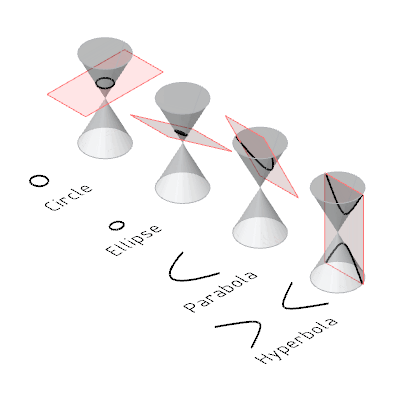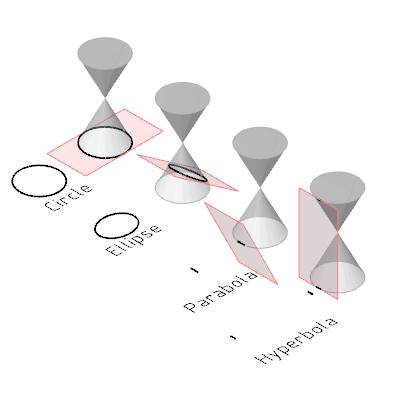
我们不禁要问,这曲线在现实中貌似属于很特殊的那一类啊,有什么用途呢?另外,既然想到切圆锥了,那随便切个西瓜、黄瓜或者别的他们那有的瓜不是可以得到更复杂的曲线吗?为什么只研究这么特殊的曲线呢?

有人说搞研究好比啃骨头,先啃软骨头,留下硬骨头给后人。这些曲线形式相对简单,可以用工具绘制。
不过你还别说,虽然简单,可能还挺有用。比如后来 16 世纪发生的两件事,将不接地气的曲线研究变成了揭示这个实现世界的工具。
是德国天文学家开普勒(Kepler)继承哥白尼的日心说,并进一步揭示出行星环绕太阳运行的轨道是一个椭圆。
意大利物理学家伽利略 (Galileo)得出物体斜抛运动的轨道是一条抛物线。
你说神不神奇,这自然界的物体运动轨迹竟然就是圆锥曲线。倍立方体问题跟这个现象貌似风马牛不相及啊,最后却惊人地联系在一起了。
古希腊数学家要是接地气一点,从事一下劳动之类的,比如抛个砖头什么的,或许老早就能发现抛物线之类的了啊。奇怪的是,他们却是从研究倍立方体这么相对抽象的问题中发现了圆锥曲线。
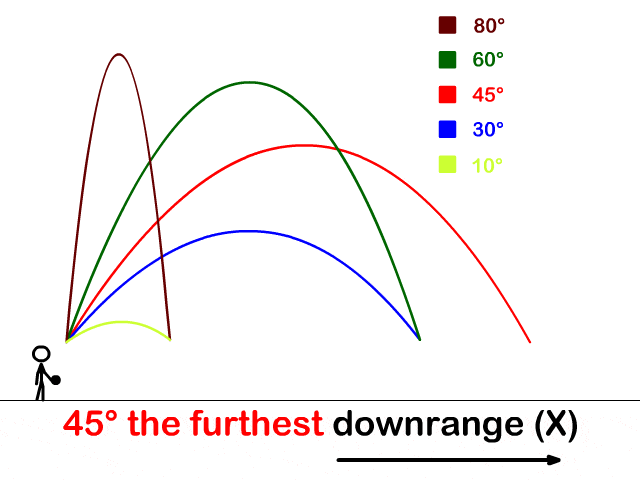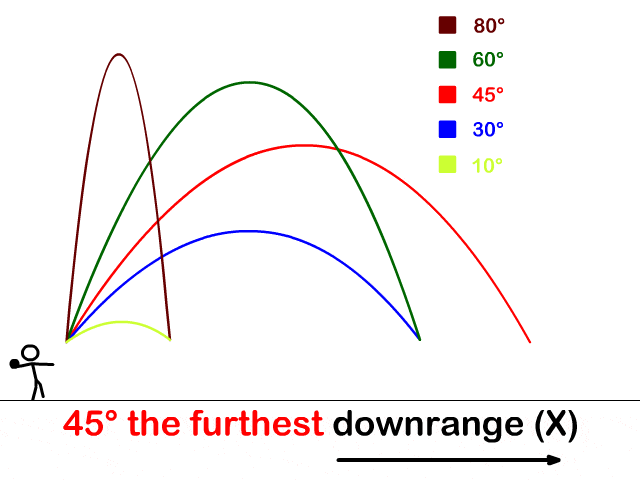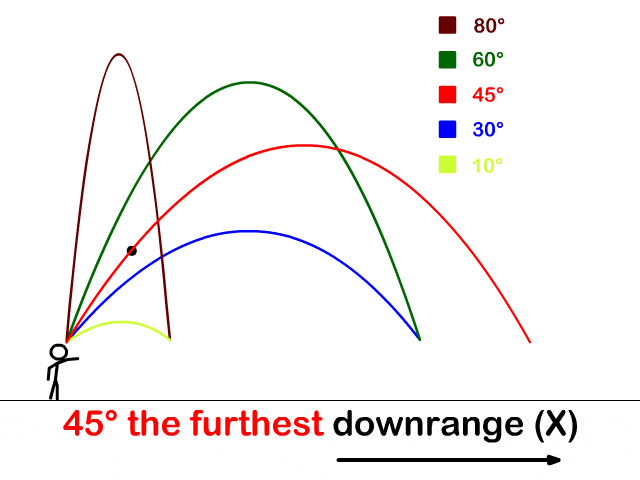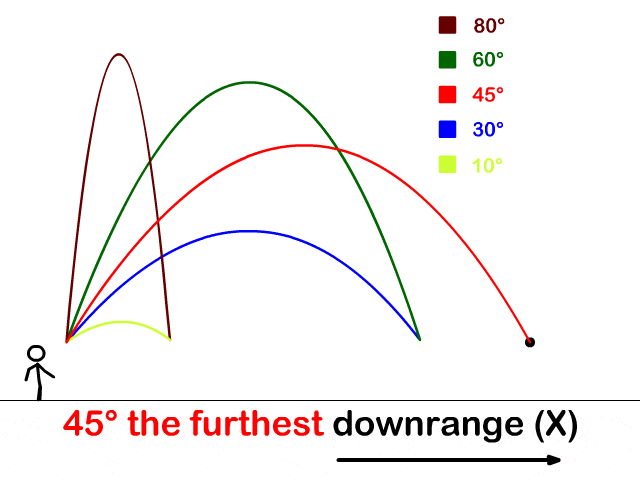
+问题
接着上面,既然通过数和量的式子发现了圆锥曲线,古希腊几何学家是不是已经认识到曲线与数量的代数运算之间的联系了呢?或者说,他们与笛卡尔的解析几何到底有什么区别呢?
问题可能还是出在他们的研究太不接地气了,过于讲究逻辑、严谨,一定程度上可以说是把自己的思维给禁锢了。比如据说柏拉图不赞成梅内赫莫斯使用机械设备来求解问题,他认为这会贬低几何学,因为在他看来几何学是人类思维的最高成就。
为了理清问题所在,我们来看一下阿基米德公理:除非一个量的若干倍可以超过另一个量,否则无法比较两个量。因此不允许一条线加上一个点,或者一个体积加上一个面积。比如,写出
在他们看来,两个数相加没什么问题,这是基本的算术运算,但一个量并不总是能加上另一个量。比如,我们用
再比如,三个量的乘积
也就是说,在他们看来只有相同类型的量才是可能相加的,而且还得对应几何量。这种对量的运算加以限制的思想,即便到了韦达那里仍然残留着。
笛卡尔的前辈,法国数学家韦达利用欧几里得的《几何原本》第一个提出了无穷等比级数的求和公式,发现了正切定律、正弦差公式、纯角球面三角形的余弦定理等,同时还发现了更加著名的韦达定理。韦达利用代数法分析几何问题的思想,正是后继者笛卡尔解析几何思想的出发点。
而笛卡尔通过引入单位 1,轻巧地打破了对量运算在思维上的限制。进而他引入了现在称为坐标系的思想来展示如何使用代数来解决几何问题。
关键一步
笛卡尔和很多前辈一样,将代数方程不是当作纯数的运算,而是指几何量的运算,用几何术语来解释所有代数运算。为了充分利用代数的力量,笛卡尔必须想出办法克服古希腊的思维限制,即在一定意义上必须与过去进行重大决裂。他为代数方程发明了一种新的几何解释,使代数学家摆脱了无法写出
他解放了自己,因此也解放了他的继任者,包括现在的我们。他选择了一条他称之为单位长度的线段,长度为
并且,还可以把长度
在这个例子中,给定一个单位线段
笛卡尔在他的著作《几何》中分析了当时的几何学与代数学各自的优缺点。他认为希腊人的几何过多地依赖于图形,而代数学却完全受法则和公式的限制,以至于阻碍了自由的思想和创造力。
他同时看到了几何的直观与推理的优势和代数机械化运算的力量。于是他为了体现存在感(吾思故吾在嘛),稍加思索创立了解析几何,并拉开了近代数学大发展的序幕。
笛卡尔的坐标系
下面我们来简单回顾下笛卡尔在他的《几何》中引入所谓坐标系的内容。其中之一个是对平面曲线的分类问题。
我们先想象有一系列曲线,其中每一类曲线都比它前面的复杂,首先认清如下事实是将所有这些曲线归并在一起并依次分类的最好办法:这些曲线上的所有的点,必定跟某个直线上的点具有一种确定的关系,而且这种关系必须用单个的方程来表示,
当方程不包含次数高于两个未知量所成的矩形或一个未知量的平方的项,则曲线属于第一类,它只包括圆、拋物线、双曲线和椭圆;
当方程包含未知量中的一个或两个的三次或四次的项,则曲线属于第二类;
当方程包含未知量中的一个或两个的五次或六次的项,则曲线属于第三类;
依此类推。
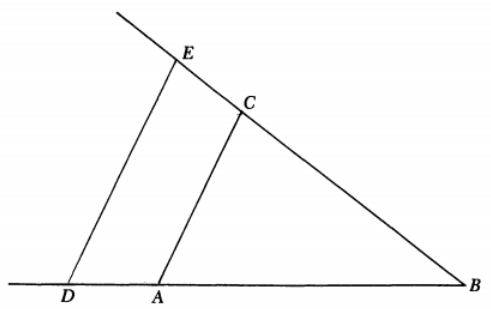
下面请看一个图,
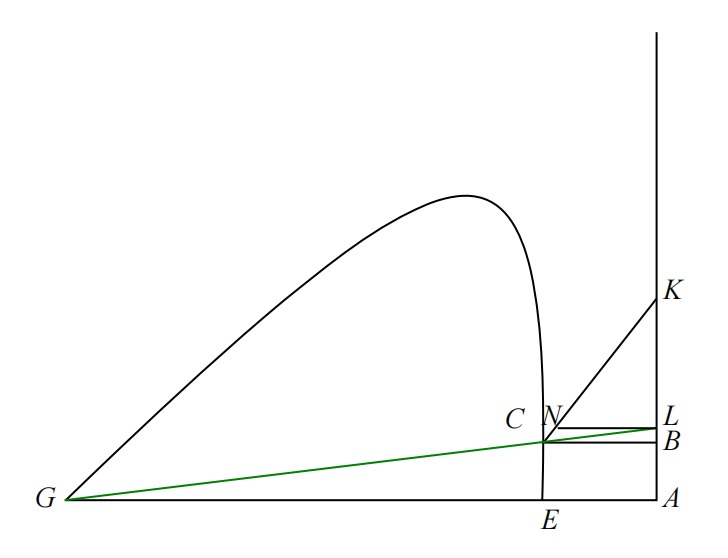
这里设
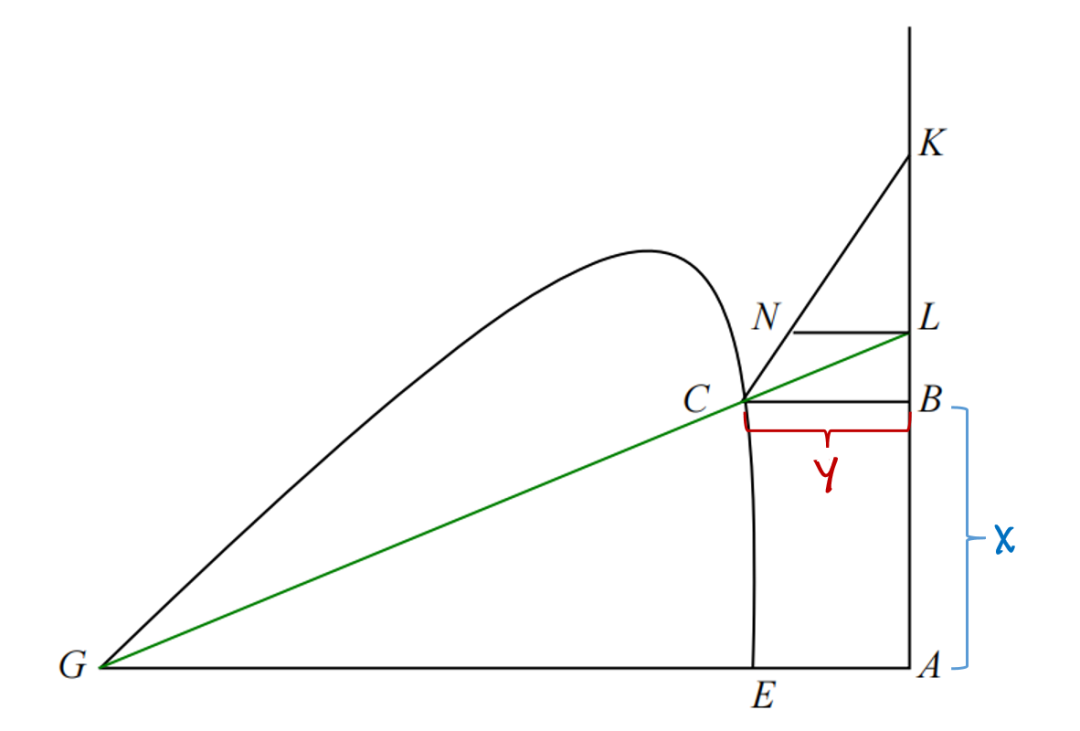
上图中
设
根据这个方程,我们知曲线
若将上述解析曲线的工具中的直线图形
注意,笛卡尔这里并没有采用直角坐标系,因为这里主要用到了相似三角形,并不需要两条线相互垂直,因此实际上任意选的直线构成的是斜角(oblique)坐标系。况且这里水平方向的距离设为 y,另一个直线上的距离设为 x。
笛卡尔借助两条直线(段),将曲线上的点与两个数构成的数对建立了对应关系,即数对中两个数满足一个方程式。在他的思想启发下,后人正式建立了坐标以及坐标系这些概念。
这里,曲线的类型与坐标系的形式(直角或斜角)以及具体坐标轴的选取没有关系,可以看成曲线固有的一个属性。当然,得到的
当然,《几何》里还有很多其他内容,但同样也没有直接引入坐标系。人家写的书叫《方法论》,几何只不过是附录之一。
+小结
笛卡儿的《几何》中虽然没有我们现在所称的笛卡儿坐标系,即平面上的直角坐标系,更没有传说中由蜘蛛网想到的三维坐标系。但他的思想和方法确实体现了解析几何的精髓,也提出了坐标系的雏形。
在笛卡尔眼中,几何问题不仅可归结成为代数形式,还可通过代数变换来揭示几何性质。
数形结合,以形辅数,以数助形!
最后引用一句话来简单评价一下笛卡尔。《古今数学思想》的作者,数学史家克莱因评价说:笛卡尔是近代第一位杰出的哲学家,是近代生物学的奠基人,是第一流的物理学家,但只偶然是个数学家。
偶尔为之,但却将之前几千年人类发展出来的几何和代数巧妙地结合起来,并一举点燃了近代数学迸发的导火索。
相关阅读
