风控算法最常见的知识WOE讲解!
想起刚入门风控时,天天对变量进行WOE变换,很多书籍和文章都讲得很详细,公式和例子都有,但他们很少直接回答:
为啥要用WOE? 不用WOE不行吗? WOE有啥神奇功效? 本文试图根据自己理解回答。
在风控用到的数据里,我们会用到两种变量:
Numerical Variable,数值变量。例如逾期金额,天数。 Categorical Variable,类别变量。例如客户职业。
在制作评分卡过程中,我们还需要把数值变量变成类别变量,例如客户年龄段,我们可以划分为[20及以下],[21-30],[31-40],[41-50],[51-60],[61-70],[70以上]七个类别,这时候我们就把数值变成了类别。这种把数值变成类别的技巧叫做分箱(binning)。
但是当把所有变量都变成类别后,这时候你也许有这个疑惑:怎么去训练一个模型呢?例如逻辑回归,只能用数值作为特征输入。怎么把类别变成数值呢?
你此刻想到的可能是one-hot encoding,但还是有问题,对于逻辑回归来说,one-hot encoding输出的矩阵太稀疏了,很难让逻辑回归有很好的效果。
这时候,我们可以试试把类别或者分箱转化成响应的数值(怎么又转回数值了?等下解答你)。这个分数必须和必须有这个特性:分数越大,代表这个变量给bad label的贡献度越大,这个贡献度,视运算符号不同,可以是正向,也可以是负向,但我们期望它们之间有个线性关系。
我们需要引入WOE编码。
一、什么是WOE
我相信在看到这篇文章时,你已经看过很多关于WOE的讲解,但为了照顾第一次研究WOE的朋友,我还是详细解释下。
WOE全称是Weight of Evidence,即证据权重,也叫作自变量的一种编码。
WOE的公式定义如下:
其中i为某个特征的第i个分箱。Bad_i为在i个分箱的bad label数量,Bad_T为总共的bad label数量。例如下面举个例子, 计算可以得到
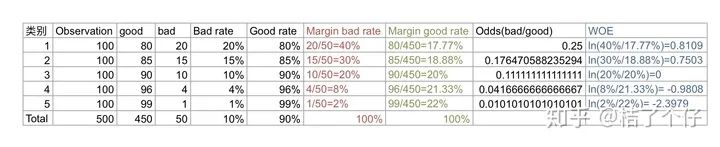
现在我们观察bad rate 和 WOE的关系,WOE越大,bad rate越高,也就是说,通过WOE变换,特征值不仅仅代表一个分类,还代表了这个分类的权重。这就回答了问题”WOE编码为啥有效“。
二、什么情况下用WOE
当然,你会有疑问:“类别变量我能理解要WOE,但对于连续变量,通过分箱变成类别变量,又通过WOE去“模拟”连续变量,这不是舍近求远吗?那我为啥不直接用原始的数值变量?
哈哈哈很聪明嘛,没被我绕进去。答案是当然可以,而且很多情况下并不会比WOE效果差。但binning+WOE能解决一个问题,就是可以把非线性的特征转化为线性。
例如在风控场景里,我们可能用到客户的年龄做特征。我们知道肯定不是年龄越大风险越高,或者年龄越大风险越低,一定是有个年龄段的风险是比其他年龄段高些。我们拿Give Me Some Credit(https://link.zhihu.com/?target=https%3A//www.kaggle.com/c/GiveMeSomeCredit/data)的数据做个分析,在数据里有个年龄字段,我们来看看年龄(age)和违约率(SeriousDlqin2yrs)的关系
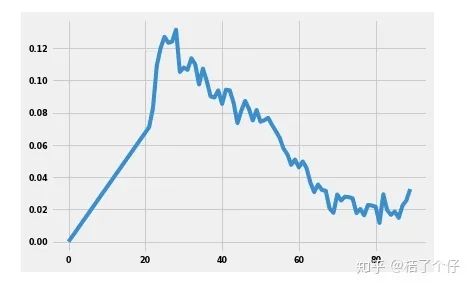
可以看到年龄和违约率并不是线性相关的。我们知道,逻辑回归的方程是:
逻辑回归拿年龄做变量,例如是年龄,训练后是固定权重值,如果是正值,那么年龄越高,的值越大,最后分数值也越大,但从上图可以看出实际不是这样的。
为了解决这个非线性的问题,我们用WOE代替年龄段,根据WOE的计算过程,我们可以知道WOE值越高的分类,违约率越高,这样就可以把非线性映射转换成线性映射。下图已经把年龄换成了WOE,可以看到WOE和违约率是线性。
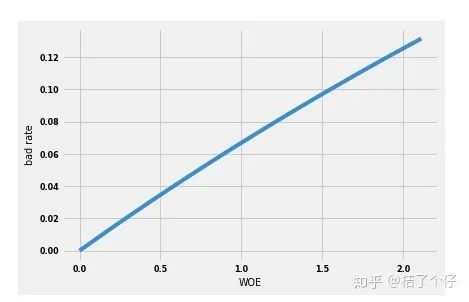
总结:WOE可以把相对于bad rate显现非线性的特征转换为线性的,这对于广义线性模型(Generalized linear model、简称GLM,我们用的线性回归,逻辑回归都算GLM)来说非常有必要。
三、WOE还有什么好处
除了可以把非线性的特征转换成线性的,WOE好处还有:
对波动不敏感。遇到异常数据亦能平稳表现。例如有个人年龄为20,不小心按键盘时按成了200,也不会产生10倍的波动。 容易操作。这是对业务人员说的,用模型计算出评分卡后,给任何不懂技术的人都能算出一个客户的风险值。
其他问题:
Q:特征有null值怎么办?
A:两种策略。1.预先fillna。2.null值单独一箱
四、总结
WOE越大,bad rate越高,也就是说,通过WOE变换,特征值不仅仅代表一个分类,还代表了这个分类的权重。这就回答了问题”WOE编码为啥有效“。 WOE可以把相对于bad rate显现非线性的特征转换为线性的,这对于广义线性模型(Generalized linear model、简称GLM,我们用的线性回归,逻辑回归都算GLM)来说非常有必要。
