风控ML[5] | WOE前的分箱一定要单调吗

今天分享的WOE单调性讨论，也是我们在建模过程中选择特征进行模型前需要考虑的一个细节问题。关于WOE，可以参考一下前面的文章回顾一下哈，《风控ML[3] | 风控建模的WOE与IV》。今天的分享主要从下面的顺序来展开。

• ✍️ 背景交代
• 🎥 WOE回顾
• 🤔 LR模型的入参一定要WOE吗？
• 🤔 WOE不单调可以进LR模型吗？
• 针对不同类型的变量
• 为什么需要WOE具备单调性
• 🏆 结论复盘

01 背景交代

相信在金融风控领域做过模型的同学，或多或少对分箱满足badrate单调性有一定的认知，特别是在用逻辑回归做A卡的时候，老司机们会经常对我们说变量要满足单调性，当变量单调了，再进行WOE转换，然后作为LR的入参喂给模型，简单训练一下就收工。但作为一个合格的风控建模大师，仅仅知道这些套路还是不够的，我们需要进一步去思考一下当中的原理，或者说是更进一步去追问一下自己：

• LR模型的入参一定要WOE吗？
• WOE转化前的变量分箱结果的badrate一定需要满足单调性吗？
• 连续变量一定要分箱？难道就不可以直接进LR模型吗？

02 WOE回顾

在我们开始拆解问题前，有一个知识点需要回顾一下，那就是WOE。

WOE是weight of evidence的缩写，是一种编码形式，首先我们要知道WOE是针对类别变量而言的，所以连续性变量需要提前做好分组（这里也是一个很好的考点，也有会说分箱、离散化的，变量优化也可以从这个角度出发）。

先给出数学计算公式，对于第i组的WOE可以这么计算：

从公式上可以看出，第i组的WOE值等于这个组的响应客户占所有响应客户的比例与未响应客户占所有未响应客户的比例的比值取对数。对于上面的公式我们还可以 简单做一下转化：

所以，WOE主要就是体现组内的好坏占比与整体的差异化程度大小，WOE越大，差异越大。

03 LR模型的入参一定要WOE吗？

The answer is no！并非所有LR的入参都需要WOE的，也可以是直接原始值入模型的。但存在即合理，为什么大家都在说要对变量进行WOE编码呢？我们可以引出下面两个问题：

• 什么情况下用WOE比较合适？
• 以及用WOE有什么好处？

我们知道，在风控领域的变量可以大致分为两类，就是数值型变量以及类别型变量，前者就是类似于年龄、逾期天数等，后者就是职业类别、行业类别等。

针对类别型变量，我们很容易可以想到使用one-hot编码来，但是这种编码方式有一定的缺陷，那就是对于枚举值特别多的变量，独热编码之后十分稀疏从而特征空间很大，另外如果丢弃一部分维度则会造成信息丢失，指不定这些是关键的信息。以上的信息说明了放入LR中很难有很好的效果。

而针对数值型变量，很多同学则会有更大的疑问，那就是为什么要分箱然后又进行WOE转换这么麻烦，反正都可以直接入模型的，何必多此一举？

当然了！这个想法也是没错的，在本小节开头也已经说明了，并非要求所有的变量都要进行WOE编码然后进入模型。而什么情况下十分适合WOE转换呢，那就是变量本身与y值并非存在直接线性关系的时候。

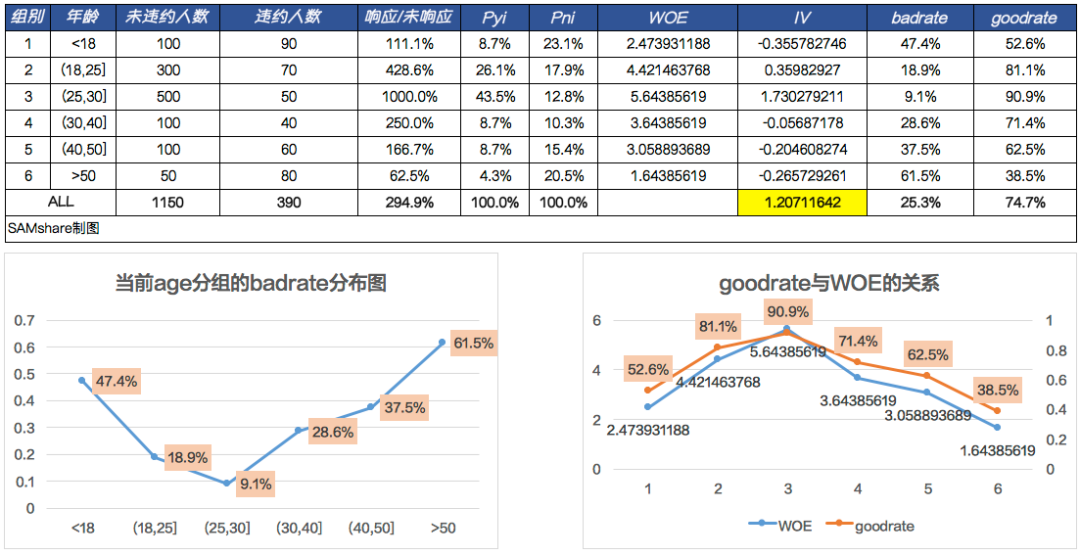
我们看上面的图，“年龄”这个字段经常性地会出现在我们的A卡模型里，作为预测一个客户信用水平的衡量指标。我们可以清楚知道，age这个变量的badrate分布，经常性会呈现“U型”，业务解释就是：年轻人和老年人的还款能力会比中年人的要低，风险也因此更高。从统计角度看，年龄与违约率，便不是一个线性关系！

我们回忆一下LR模型（Logistic Regression），从本质上讲，LR就是经过对训练集的学习，得到一组权值w，当有新的一组数据x输入时，根据公式计算出结果，然后经过Sigmoid函数判断这个数据所属的类别。

假如我们的年龄就是上面的x1，并且模型只有一个变量，那么随着x1的变大，的值也会不断变大，而不是像上图一样呈现“U型”，说明了这是一个非线性的问题，但如果我们对年龄进行WOE转换，就可以看到如右图所示的那样，随着WOE的增大，goodrate也增大这种线性关系（badrate=1-goodrate，因此和badrate也是线形关系）。

以上也是使用WOE编码的一个最大好处，也就是把badrate呈现非线性的变量转换为线形，便于理解也便于后续模型求解。此外，WOE编码还有一个好处，那就是具有“容错性”，因为WOE编码其实也可以理解为需要预先分箱，那么对于异常值没那么敏感，对于单个变量的异常波动不会有太大反应。

04 WOE不单调可以进LR模型吗？

那么我们回到最初的问题，那就是如标题所说的：WOE前的分箱一定要单调吗？结论是不一定需要单调。要深入了解这答案，我们可以看看下面两个讨论：

0401 针对不同类型的变量

1）针对类别变量😋

类别变量可以分有序和无序变量。

针对有序类别变量，比如像学历，我们分箱的时候要保证原始顺序的前提下，进行不同原始组别的合并，完成分箱，然后需要看分箱的badrate单调性，最后才来看WOE单调性情况。

针对无序类别变量，无序类别变量又可以根据枚举值的多少拆分为两类：多枚举无序类别变量和少枚举无序类别变量。无论是哪一种，我们都可以根据对每个枚举值的badrate统计得到其量化指标，然后根据badrate进行适当的类别合并，完成分箱操作，这时候的分箱结果，天然单调！而针对少枚举无序类别变量，我们还可以根据业务认识，进行类别的合并，比如像中国大区字段（华南、华北等），WOE编码后，也不做严格的单调性要求。

2）针对数值变量😆

进行合适的分箱算法进行分箱后的bin，需要满足badrate单调性，然后才进行WOE编码。不过呢，这个也不是严格要求的。

0402 为什么需要WOE具备单调性

WOE不一定都需要是单调的，只要从业务角度可以解释得通，那就没有问题！就好像上面的那个栗子，年龄字段，WOE就不是单调的，但从业务上可以解释得通，那就没有问题！

如果从业务上解释是需要单调性，但分组后的WOE并没有单调，那么这时候有两条路可以选择，一是重新分组然后重新计算WOE，二是放弃这个变量。

最后提一下，如果不单调的变量不进行WOE编码直接进入LR模型，一般都是很难求解的，因为很难找到一个线性公式来描述关系。

05 结论复盘🏆

1）LR模型的入参不一定都要WOE转换，直接进行模型也是可以的，只是遇上不单调的变量会比较难求解罢了，可选择丢弃。

2）使用WOE编码的一个最大好处是把badrate呈现非线性的变量转换为线形，便于理解也便于后续模型求解，进行了WOE编码的模型对于异常值没那么敏感，单个变量的异常波动不会对模型造成很大反应。

3）WOE并不一定都需要是单调的，只要从业务角度可以解释得通即可。