Ising 模型及马尔科夫链蒙特卡罗方法-技术圈

这个月刚出炉的诺贝尔物理学奖让大家重新认识了一个主题，复杂系统。乔治·帕里西（Giorgio Parisi）于上世纪 80 年代对自旋玻璃作了深入研究，发现了随机现象背后的隐藏规则，被认为是对复杂系统理论最重要的贡献之一。

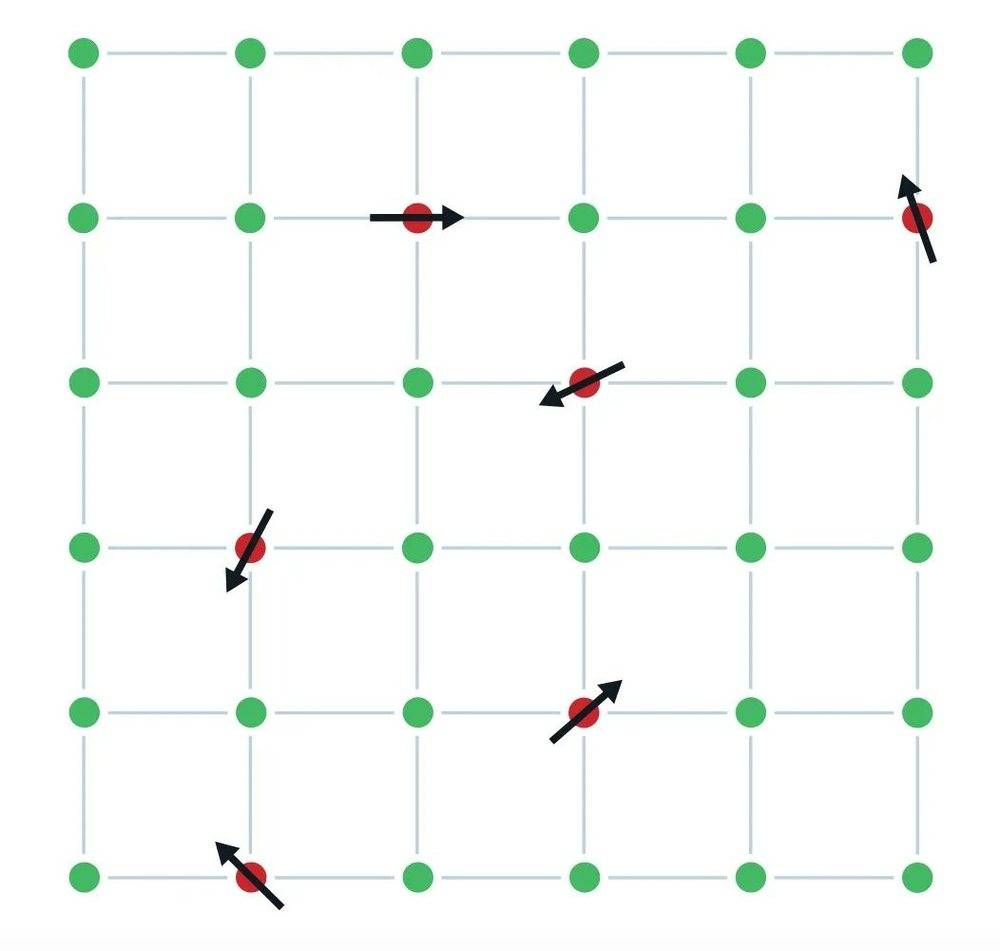
自旋玻璃是一种特殊类型的金属合金，其中铁原子随机混合进铜原子网格。每一个铁原子的行为都像一个小磁铁（或者说自旋），受到邻近铁原子的影响。在普通磁铁中，所有自旋都指向同一方向，但在自旋玻璃中，一些自旋对想要指向同一方向，而另一些自旋对想要指向相反方向。那么，它们如何趋于平衡呢？

自旋玻璃的奇特性质为复杂系统提供了一个模型，在这些系统中，各个部分必须在各种反作用力间达到平衡。帕里西对自旋玻璃结构的基本发现非常深刻，使人们能够理解和描述许多不同的、显然完全随机的材料和现象，不仅可用于物理学领域，而且在数学、生物学、神经科学和机器学习等领域也大显身手。

帕里西还研究了许多其他现象，如：为什么冰河期会周期性地重复出现？对于混沌和湍流系统，是否存在更具一般性的数学描述？数千只椋鸟的咕哝声是如何形成特定模式的？这些问题看上去似乎与自旋玻璃相去甚远。但帕里西说，他的大部分研究都关注简单行为如何导致复杂的整体行为，无论对自旋玻璃还是对椋鸟群都同样适用。

为了对所谓的复杂系统有所了解，我们来看一个这次拿下诺贝尔奖的自旋玻璃模型的简化版本，即经典的 Ising 模型。

1Ising 模型简史

Ising 模型的提出是为了解释铁磁物质的相变，即磁铁在加热到一定临界温度以上会出现磁性消失的现象，而降温到临界温度以下又会表现出磁性。这种有磁性、无磁性两相之间的转变，是一种连续相变。

Ising 模型假设铁磁物质是由一堆规则排列的小磁针构成，每个磁针只有上下两个方向（自旋）。相邻的小磁针之间通过能量约束发生相互作用，同时又会由于环境热噪声的干扰而发生磁性的随机转变。

涨落的大小由关键的温度参数决定，温度越高，随机涨落干扰越强，小磁针越容易发生无序而剧烈地状态转变，从而让上下两个方向的磁性相互抵消，整个系统消失磁性。

如果温度很低，则小磁针相对宁静，系统处于能量约束高的状态,大量的小磁针方向一致,铁磁系统展现出磁性。而当系统处于临界温度的时候，Ising 模型表现出一系列幂律行为和自相似现象。

由于 Ising 模型的高度抽象，人们可以很容易地将它应用到其他领域之中。

例如，人们将每个小磁针比喻为某个村落中的村民，而将小磁针上、下的两种状态比喻成个体所具备的两种政治观点（例如对 A,B 两个不同候选人的选举），相邻小磁针之间的相互作用比喻成村民之间观点的影响。环境的温度比喻成每个村民对自己意见不坚持的程度。这样，整个 Ising 模型就可以建模该村落中不同政治见解的动态演化（即观点动力学 opinion dynamics）。在社会科学中，人们已经将 Ising 模型应用于股票市场、种族隔离、政治选择等不同的问题。
另一方面，如果将小磁针比喻成神经元细胞，向上向下的状态比喻成神经元的激活与抑制，小磁针的相互作用比喻成神经元之间的信号传导，那么，Ising 模型的变种还可以用来建模神经网络系统，从而搭建可适应环境、不断学习的机器，如 Hopfield 网络和 Boltzmann 机之类。

Ising 模型不仅仅是一个统计物理模型，它更是一个建模各种复杂系统模型的典范。

2模型参数

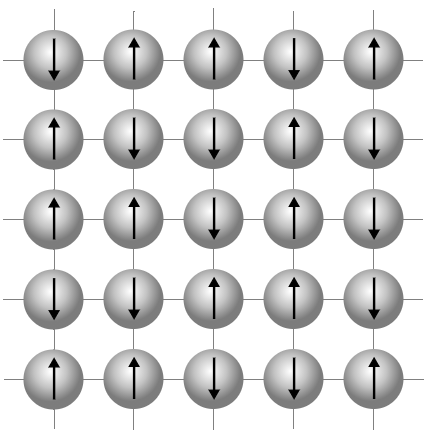
假设第个节点是一个小磁针（或者一个村民），每个小磁针有上下两种状态（村民有上,下两种意见），我们用来表示这个状态，并且

\displaystyle{ s_i=\left\{\begin{array}{ll} +1 & \\ -1 & \end{array}\right. }

表示磁针朝上或者朝下。网格上相邻的两个小磁针可以发生耦合作用。

+几股势力

用于统摄所有小磁针的一个磁场，表示整体的影响或约束，本文姑且称它为正能量（这里的正不是 +，是以它的方向为正统）。
相邻小磁针的相互影响，表示局部的影响或约束，本文姑且称为耦合能量。
外界的干扰势力，比如外界温度越高，个体小磁针越亢奋，正能量和耦合能量对它的统摄和约束能力就越小。

一个系统在这三股势力的综合影响下趋于平衡，那么怎么将这三股势力统一用公式表达出来呢？

+总能量

我们先看前两股势力：

如果小磁针方向与正能量方向一致，则总能量降低；
如果两个相邻小磁针的状态一致，则系统的总能量减个单位，否则就增个单位。

综合这两点，将总能量定义为，

\displaystyle{E_{\{s_i\}} = - J\sum_{\langle i,j \rangle }{s_is_j} - H\sum_{i}^N{s_i}}

其中，

为一个能量耦合常数，表示系统处于状态组合下的总能量。对于边，如果，则总能量减少。
参数表示正能量，某个小磁针的方向如果与正能量一致，则总能量减少。

我们看个例子，假设系统中只有个小磁针，两两相连形成一个三角形，如下图所示。

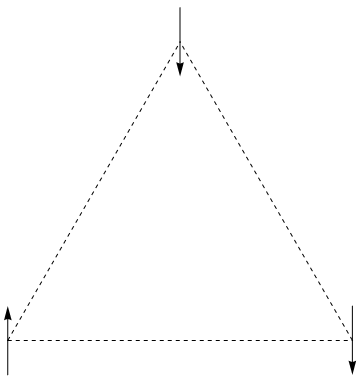
每个小磁针有两种可能状态，那么所有的状态组合就包括：

\displaystyle{ \{s_i\}=\{\\+1+1+1,\\+1+1-1,\\+1-1+1,\\+1-1-1,\\-1-1+1,\\-1+1+1,\\-1+1-1,\\-1-1-1 \} }

那么这种状态组合，对应个能量值，分别为：

\begin{aligned} E_{\{+1+1+1\}}&=-3J-3H,\\ E_{\{+1+1-1\}}&=J-H, \\ E_{\{+1-1+1\}}&=J-H, \\ E_{\{+1-1-1\}}&=J+H, \\ E_{\{-1+1+1\}}&=J-H, \\ E_{\{-1+1-1\}}&=J+H, \\ E_{\{-1-1+1\}}&=J+H, \\ E_{\{-1-1-1\}}&=-3J+3H \end{aligned}

由能量项可知，小磁针相互之间以及与方向一致的话，系统的能量就低。上面例子中，假设是正的，那么是能量最小的状态。

沿用村民的比喻来说，系统的能量相当于村民观点存在的冲突的数量。如果两个相邻的村民意见不一致，总冲突数就，否则就减。而外场建模了观点的媒体宣传效应，如果村民的观点与舆论宣传一致，则能量越低，因此也越和谐。

+外部干扰

但是，系统的演化并不完全由总能量决定。由于小磁针暴露于外部环境中，热涨落又会引起小磁针的状态随机反转。可以用温度来衡量这种环境影响的随机性，即越高小磁针表现得越随机。

于是，每个小磁针就挣扎于这两种不同的势力之间：

假如外部干扰势力温度趋于，则每个小磁针都会与外场相一致，那么，最终系统将处于全是或者全是的状态。
假如特别高，而和又特别小，则邻居间的作用可以忽略，每个小磁针都将趋于随机取值。

因此，整个 Ising 模型就有两个参数和来设定环境温度和磁场强度。在村民的比喻中，温度相当于村民进行观点选择的自由程度，温度越高，村民选择观点越独立随机，越不受周边邻居的影响。

3统一建模

Ising 模型中并没有针对每个小磁针设定其状态转变的规则，而是先让每个小磁针的状态发生随机变化，再根据能量来依概率接受这种状态变化。在 Ising 模型中，小磁针的自旋状态分布取决于温度，并遵循 Boltzmann 分布：

状态频率 \; \propto \; \exp\left(-\frac{E}{kT}\right)

其中是玻尔兹曼常数，是环境温度，是磁化的总能量。当没有上文中提及地外部磁场时，给定耦合参数，磁化能量为：

E=-J \sum_{\text {小磁针}_i} \sum_{\text {相邻小磁针}_j}\left(s_{\text {i}} \cdot s_{\text {j}}\right)

简写为，

E=-J \sum_{\langle i, j\rangle} s_{i} s_{j}

通过在不同温度下多次运行 MCMC 分析来确定作为温度函数的平均磁化强度。可以通过迭代每个可能的状态，计算给定磁化强度的能量，然后根据其频率再作加权平均，相当于暴力计算系统的平衡磁化强度。但是，这样做往往不现实，因为需要太多的计算。即使网格非常小，比如，它也有 100 个位置，因此总共有种不同状态。

+随机选状态

因此，与其遍历所有可能的状态，不如随机选择一组状态并按其频率加权计算平均值。这样做的问题是效率低下。玻尔兹曼分布并不均匀：它偏向于较低的能量。理想情况下，对于更频繁出现的状态，我们希望用一种方法来更频繁地找出它的自旋状态。

4Metropolis-Hastings

而这正是核物理学家 Nicholas Metropolis 和他的合作者的贡献。该方法最初发表于 1953 年。他们在曼哈顿项目的工作中率先引入了蒙特卡罗方法和马尔可夫链蒙特卡罗方法。

他们使用他们新创建的技术在状态空间中随机游走，更频繁地访问更频繁出现的自旋状态，并大大加快计算速度。用他们的话来说：

我们不是随机选择状态，然后用对其进行加权；
而是以概率随机地选择状态，然后均匀加权。

不过，他们并没有解释为什么这样做可行。至于被命名为 Metropolis-Hastings 的原因，算法名字中加入 Hastings 意味着是承认统计学家 W. K. Hastings 在 1970 年的贡献，他使得该技术背后的理论最终得到解释和概括。从具有密度的分布中采样的方法的主要特征是：

计算依赖于的地方仅仅是以这样的比率形式，其中和是样本点。因此，不需要知道归一化常数，不需要对进行因式分解，并且这些方法很容易在计算机上实现。
通过模拟马尔可夫链获得样本序列。因此，产生的样本是相关的，对标准差的估计和对误差的估计可能需要比独立样本更加小心。

这个想法用到 Ising 模型上涉及到的物理学是自旋状态遵循玻尔兹曼分布，即

状态频率 \; \propto \; \exp (-E / k T)

具体取值如下，

：小磁针晶格的状态
：状态的频率分布
：无量纲温度
：所有相邻自旋的总和

用上面这些符号更新公式，

p(x) \propto \exp \left(-\frac{H(x)}{\widetilde{T}}\right)=\exp \left(-\frac{1}{\widetilde{T}} \sum_{\langle i, j\rangle} s_{i} s_{j}\right)

这里只能说它们之间是成正比的，而要像知道某个特定自旋状态发生的概率，需要将它除以所有可能的状态，以便概率加起来为，即

p(x)=\frac{\exp (-H(x) / \widetilde{T})}{\sum_{\text {all } x} \exp (-H(x) / \widetilde{T})}

但问题是我们并不知道分母，这也是最初困扰贝叶斯统计学家之处。幸运的是，我们可以使用 MCMC。正如 Hastings 所说，

计算仅仅以这个比率形式依赖于，其中和是样本点。因此，不需要知道归一化常数，不需要对进行因式分解，并且这些方法很容易在计算机上实现，

+具体实现

对于 Ising 模型，Metropolis-Hasting 算法遵循以下步骤：

1、选择一个起始自旋状态。

2、选择一个新的自旋状态。

3、根据新状态与旧状态的相对概率，随机地决定采用新状态还是保留旧状态。

4、重复步骤 2 和 3，直到收敛。实际上这里往往是设定一个步。

其中，关于的概率质量函数是，

p(x)=\frac{\exp (-H(x) / \widetilde{T})}{\sum_{\text {all } x} \exp (-H(x) / \widetilde{T})}

这意味着对于第 3 步，似然比是

\frac{p\left(x^{\prime}\right)}{p(x)}=\left.{ \frac{\exp \left(-H\left(x^{\prime}\right) / \widetilde{T}\right)}{\sum_{\text {all } x} \exp (-H(x) / \widetilde{T})}} \middle/ \frac{\exp (-H(x) / \widetilde{T})}{\sum_{\operatorname{all} x} \exp (-H(x) / \widetilde{T})} \right.

这是一个比值，因此避免了对所有状态求和

\frac{p\left(x^{\prime}\right)}{p(x)}=\frac{\exp \left(-H\left(x^{\prime}\right) / \widetilde{T}\right)}{\exp (-H(x) / \widetilde{T})}

得到似然比为，

\frac{p\left(x^{\prime}\right)}{p(x)}=\exp \left(-\frac{H\left(x^{\prime}\right)-H(x)}{\widetilde{T}}\right)

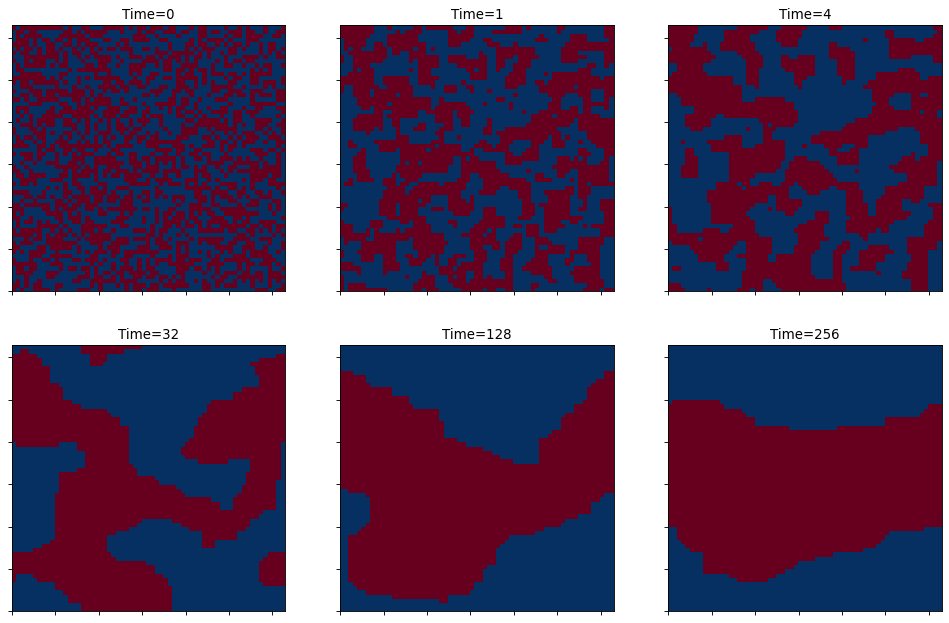
算法按照上述比率来选择新旧状态和，从而以适当的加权概率游走马尔可夫链。Hastings 在文献中描述了几种方案，但表示 Metropolis 他们的选择是最有效的。算法中是以如下概率从转移到，

p\left(\right. x 变更到 \left.x^{\prime}\right)=\left\{\begin{array}{cc}1 & \text { 如 } H\left(x^{\prime}\right)-H(x)<0 & \text { (能量变低) } \\ \exp \left(-\frac{H\left(x^{\prime}\right)-H(x)}{\widetilde{T}}\right) & \text { 如 } H\left(x^{\prime}\right)-H(x) \geq 0 & \text { (能量变高) }\end{array}\right.

5简单实现

针对 Ising 模型的简单模拟网上 Python 代码很多，比如 https://rajeshrinet.github.io/blog/2014/ising-model/。

import numpy as np
from numpy.random import rand
import matplotlib.pyplot as plt

%matplotlib inline
# Simulating the Ising model

class Ising():
    ''' Simulating the Ising model '''    
    
    ## monte carlo moves
    def mcmove(self, config, N, beta):
        ''' This is to execute the monte carlo moves using 
        Metropolis algorithm such that detailed
        balance condition is satisified'''
        for i in range(N):
            for j in range(N):            
                    a = np.random.randint(0, N)
                    b = np.random.randint(0, N)
                    s =  config[a, b]
                    nb = config[(a+1)%N,b] + config[a,(b+1)%N] + config[(a-1)%N,b] + config[a,(b-1)%N]
                    cost = 2  s  nb
                    if cost < 0:
                        s *= -1
                    elif rand() < np.exp(-cost*beta):
                        s *= -1
                    config[a, b] = s
        return config
    
    def simulate(self):   
        ''' This module simulates the Ising model'''
        N, temp     = 64, .4        # Initialse the lattice
        config = 2*np.random.randint(2, size=(N,N))-1
        f = plt.figure(figsize=(15, 15), dpi=80);    
        self.configPlot(f, config, 0, N, 1);
        
        msrmnt = 1001
        for i in range(msrmnt):
            self.mcmove(config, N, 1.0/temp)
            if i == 1:       self.configPlot(f, config, i, N, 2);
            if i == 4:       self.configPlot(f, config, i, N, 3);
            if i == 32:      self.configPlot(f, config, i, N, 4);
            if i == 128:     self.configPlot(f, config, i, N, 5);
            if i == 256:    self.configPlot(f, config, i, N, 6);
                  
    def configPlot(self, f, config, i, N, n_):
        ''' This modules plts the configuration once passed to it along with time etc '''
        X, Y = np.meshgrid(range(N), range(N))
        sp =  f.add_subplot(3, 3, n_ )  
        plt.setp(sp.get_yticklabels(), visible=False)
        plt.setp(sp.get_xticklabels(), visible=False)      
        plt.pcolormesh(X, Y, config, cmap=plt.cm.RdBu);
        plt.title('Time=%d'%i); plt.axis('tight')    
    plt.show()

rm = Ising()
rm.simulate()

运行结果如下，