牛顿迭代法的可视化详解-技术圈

来源：DeepHub IMBA
本文约1800字，建议阅读10分钟
本文利用可视化方法，为你直观地解析牛顿迭代法。

牛顿迭代法（Newton's method）又称为牛顿-拉夫逊（拉弗森）方法（Newton-Raphson method），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。

以 Isaac Newton 和 Joseph Raphson 命名的 Newton-Raphson 方法在设计上是一种求根算法，这意味着它的目标是找到函数 f(x)=0 的值 x。在几何上可以将其视为 x 的值，这时函数与 x 轴相交。

Newton-Raphson 算法也可以用于一些简单的事情，例如在给定之前的连续评估成绩的情况下，找出预测需要在期末考试中获得 A 的分数。其实如果你曾经在 Microsoft Excel 中使用过求解器函数，那么就使用过像 Newton-Raphson 这样的求根算法。另外一个复杂用例是使用 Black-Scholes 公式反向求解金融期权合约的隐含波动率。

Newton-Raphson公式

虽然公式本身非常简单，但如果想知道它实际上在做什么就需要仔细查看。

首先，让我们回顾一下整体方法：

1. 初步猜测根可能在哪里？

2. 应用 Newton-Raphson 公式获得更新后的猜测，该猜测将比初始猜测更接近根。

3. 重复步骤 2，直到新的猜测足够接近真实值。

这样就足够了吗？Newton-Raphson 方法给出了根的近似值，尽管通常它对于任何合理的应用都足够接近！但是我们如何定义足够接近？什么时候停止迭代？

一般情况下Newton-Raphson 方法有两种处理何时停止的方法。1、如果猜测从一个步骤到下一步的变化不超过阈值，例如 0.00001，那么算法将停止并确认最新的猜测足够接近。2、如果我们达到一定数量的猜测但仍未达到阈值，那么我们就放弃继续猜测。

从公式中我们可以看到，每一个新的猜测都是我们之前的猜测被某个神秘的数量调整了🔮。如果我们通过一个例子来可视化这个过程，它很快就会清楚发生了什么!

作为一个例子，让我们考虑上面的函数，并做一个 x=10 的初始猜测（注意这里实际的根在 x=4）。Newton-Raphson 算法的前几个猜测在下面的 GIF 中可视化👇

我们最初的猜测是 x=10。为了计算我们的下一个猜测，我们需要评估函数本身及其在 x=10 处的导数。在 10 处求值的函数的导数只是简单地给出了该点切线曲线的斜率。该切线在 GIF 中绘制为 Tangent 0。

看下一个猜测相对于前一个切线出现的位置，你注意到什么了吗？下一个猜测出现在前一个切线与 x 轴相交的位置。这就是 Newton-Raphson 方法的亮点！

事实上， f(x)/f'(x) 只是给出了我们当前猜测与切线穿过 x 轴的点之间的距离（在 x 方向上）。正是这个距离告诉我们每次更新的猜测是多少，正如我们在 GIF 中看到的那样，随着我们接近根本身，更新变得越来越小。

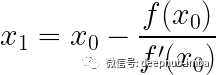
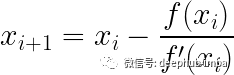
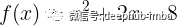
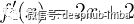
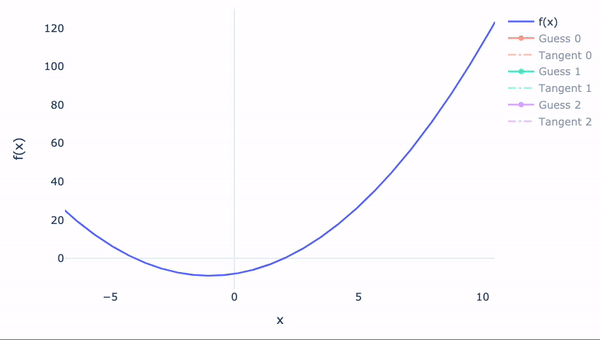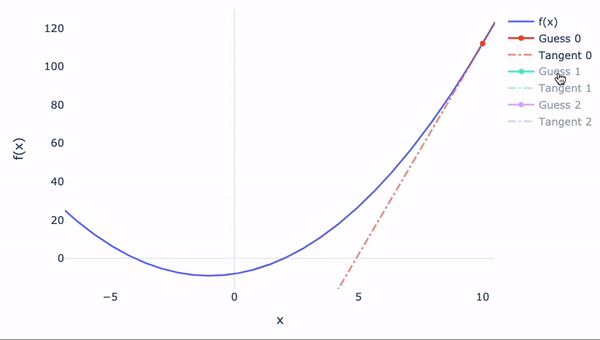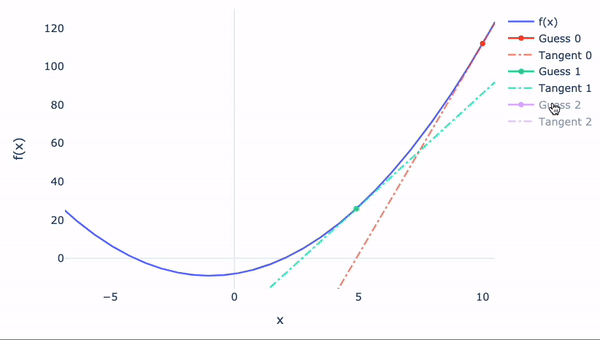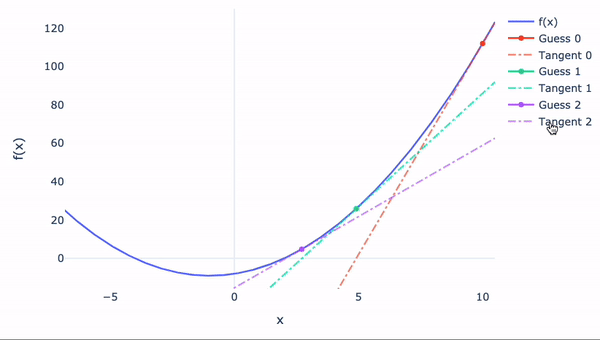
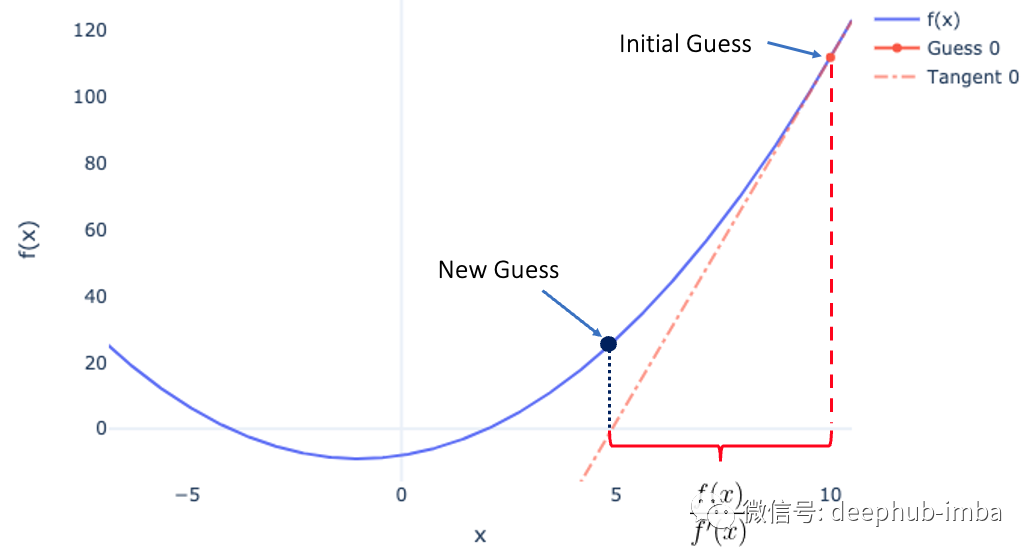
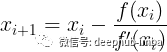
如果函数无法手动微分怎么办？

上面的例子中是一个很容易用手微分的函数，这意味着我们可以毫无困难地计算 f'(x)。然而，实际情况可能并非如此，并且有一些有用的技巧可以在不需要知道其解析解的情况下逼近导数。

这些导数逼近方法超出了本文的范围，可以查找有关有限差分方法的更多信息。

问题

敏锐的读者可能已经从上面的示例中发现了一个问题，示例函数有两个根（x=-2 和 x=4），Newton-Raphson 方法也只能识别一个根。牛顿迭代会根据初值的选择向某个值收敛，所以只能求出一个值来。如果需要别的值，是要把当前求的根带入后将方程降次，然后求第二个根。这当然是一个问题，并不是这种方法的唯一缺点：

牛顿法是一种迭代算法，每一步都需要求解目标函数的Hessian矩阵的逆矩阵，计算比较复杂。
牛顿法收敛速度为二阶，对于正定二次函数一步迭代即达最优解。
牛顿法是局部收敛的，当初始点选择不当时，往往导致不收敛；
二阶Hessian矩阵必须可逆，否则算法进行困难。

与梯度下降法的对比

梯度下降法和牛顿法都是迭代求解，不过梯度下降法是梯度求解，而牛顿法/拟牛顿法是用二阶的Hessian矩阵的逆矩阵或伪逆矩阵求解。从本质上去看，牛顿法是二阶收敛，梯度下降是一阶收敛，所以牛顿法就更快。如果更通俗地说的话，比如你想找一条最短的路径走到一个盆地的最底部，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。（牛顿法目光更加长远，所以少走弯路；相对而言，梯度下降法只考虑了局部的最优，没有全局思想）。

那为什么不用牛顿法替代梯度下降呢？

牛顿法使用的是目标函数的二阶导数，在高维情况下这个矩阵非常大，计算和存储都是问题。
在小批量的情况下，牛顿法对于二阶导数的估计噪声太大。
目标函数非凸的时候，牛顿法容易受到鞍点或者最大值点的吸引。

实际上目前深度神经网络算法的收敛性本身就是没有很好的理论保证的，用深度神经网络只是因为它在实际应用上有较好的效果，但在深度神经网络上用梯度下降法是不是能收敛，收敛到的是不是全局最优点目前还都是无法确认的。并且二阶方法可以获得更高精度的解，但是对于神经网络这种参数精度要求不高的情况下反而成了问题，深层模型下如果参数精度太高，模型的泛化性就会降低，反而会提高模型过拟合的风险。

作者：Rian Dolphin

编辑：黄继彦