牛顿口中的巨人都有哪些人?
牛顿和胡克（身材矮小）之间因发现万有引力定律的优先权闹得不愉快，在他们貌似绅士谦逊但暗藏讥讽的通信中牛顿说过一句话：
如果我比别人看得更远，那是因为我站在巨人的肩膀上。
这话显然在讥讽胡克，但的确也是事实。比如在物理上，牛顿的成就建立在伽利略、开普勒等巨人的研究上。
而本文想说的是在数学上，也就是在构建微积分这个大杀器方面牛顿也不是从头干起，那么这里头是不是也有巨人呢？
回答是肯定的。
牛顿在读大学那会儿，数学上很大程度是靠自学的。他学习了欧几里得的《原本》、笛卡儿的《几何》、沃利斯的《无穷算术》、巴罗的《数学讲义》等许多数学家的著作。而牛顿自己说过对他影响巨大的要数笛卡儿的《几何》和沃利斯的《无穷算术》。因为，正是它们将牛顿引导到当时的前沿数学，解析几何和几何算术化。
我们不禁要问，从《原本》到《几何》，历经近两千年，这是数学知识积累后的突破，还是思想上的突破？
1 古希腊为什么没有坐标几何？
我们知道，古希腊的几何很厉害，但他们擅长于演绎逻辑，建立了公理化体系，为人类数学和科学建立了不世之功。
然鹅，他们的几何为什么不包括坐标几何（解析几何）呢？
坐标几何的基本思想是用方程来表示曲线，希腊人则是利用曲线来研究代数，例如梅内克缪斯受希波克拉底处理倍立方体问题的启发，利用抛物线和双曲线的交点得到 。
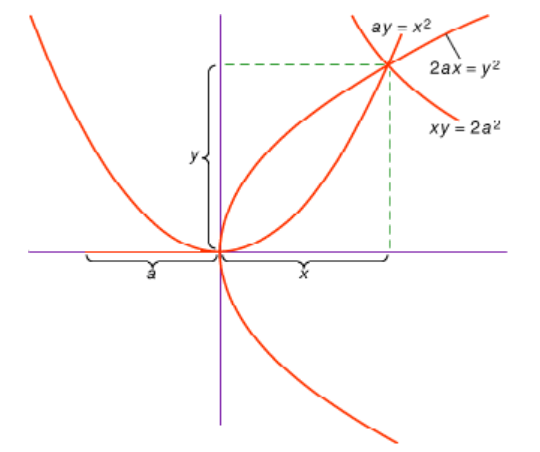
信仰万物皆数的毕达哥拉斯强调数的比例论，然而由于不可公度的发现，他们的理论遭受危机。
这也导致数的理论与几何空间的理论之间的分裂，古希腊转向几何学。特别是在欧多克索斯提出以几何量为基础的比例理论后，在古希腊人看来，几何比代数的逻辑基础更加牢固。
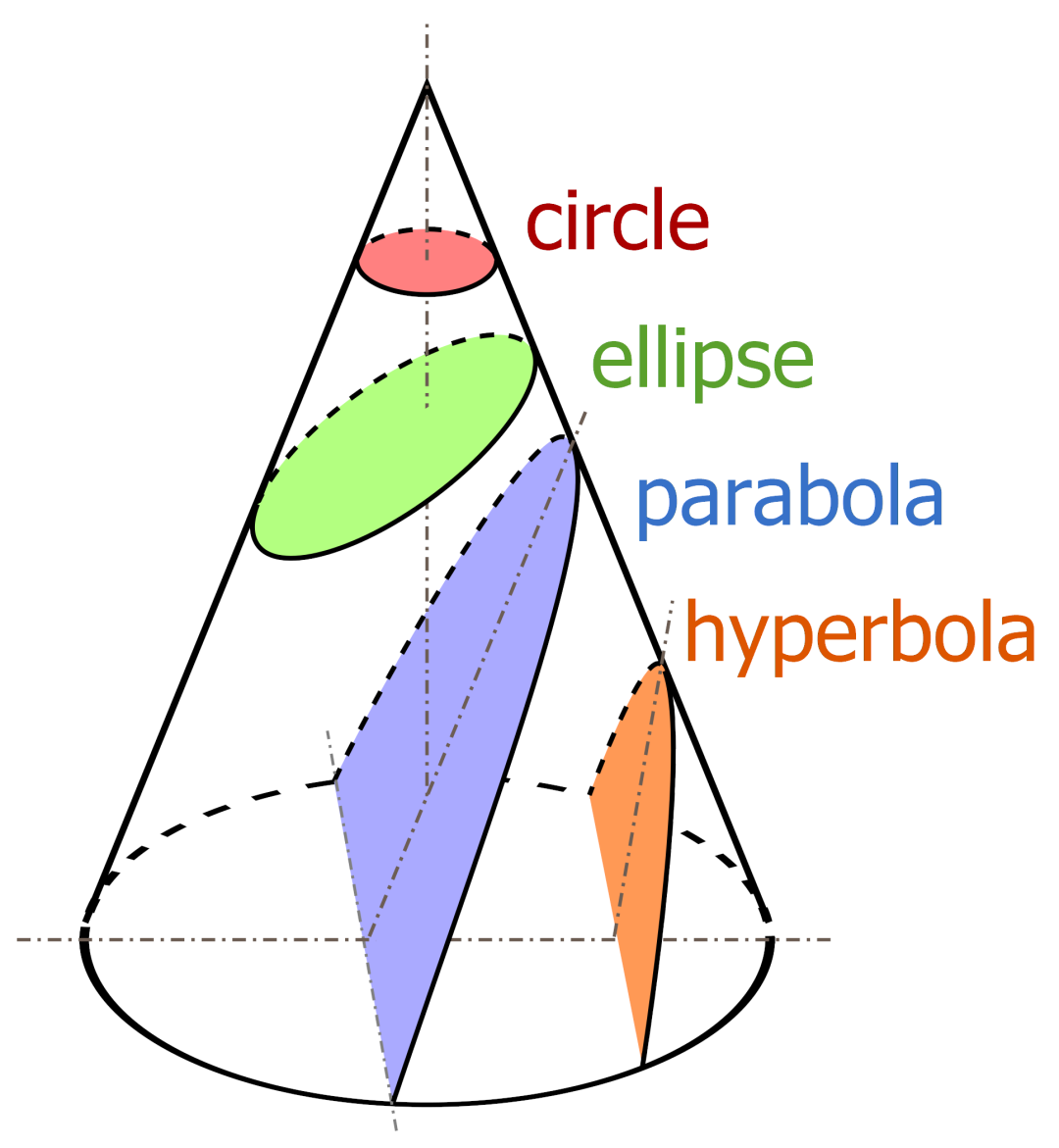
那么古希腊数学家在没有坐标的情况下是怎么研究圆锥曲线的？
希腊人偶然利用曲线来研究代数，例如梅内克缪斯受希波克拉底处理倍立方体问题的启发，发现圆锥曲线，并利用抛物线和双曲线的交点得到 。后来，阿波罗尼奥斯在总结前人成果的基础上完成了著名的大作《圆锥曲线论》。通过几何量的比例，如长度的比例、面积的比例等来分析截线的几何性质。不是通过坐标以及距离来计算的，因为他们排斥代数。虽然可以认为本质上是一致的，只是他们不使用数，而是使用几何量的比例，两者之间被割裂。
2 笛卡尔的坐标几何
公元前 146 年，罗马吞并希腊，几百年后罗马分裂成东、西两个。
不知道咋肥事，数学的事情仿佛被按了暂停键。此时数学，特别是代数在东方仍有发展，这对西欧数学会有一定影响。
直到 16 世纪，力学方面的研究开始驱使数学家研究诸如重心之类的问题，才又开始恢复进展。
荷兰工程师斯蒂文（Simon Stevin，1548 - 1620），在计算三角形重心的过程中改进了古希腊人的穷竭法，放弃归谬法，使用极限思想；《静力学原理》一书中，使用了平行四边形法则。
意大利数学家瓦莱里奥（Valerio，1552 - 1618)，运用阿基米德法求各种旋转体的重心和体积，重新燃起了人们对古希腊数学的热情。
德国天文学家开普勒（Kepler，1571 - 1630）支持日心说，并从大量天文观察数据中发现了行星运动三大定律。
我们来欣赏一下从地球上看到的各大行星在天球上的优美舞姿（轨迹图）。
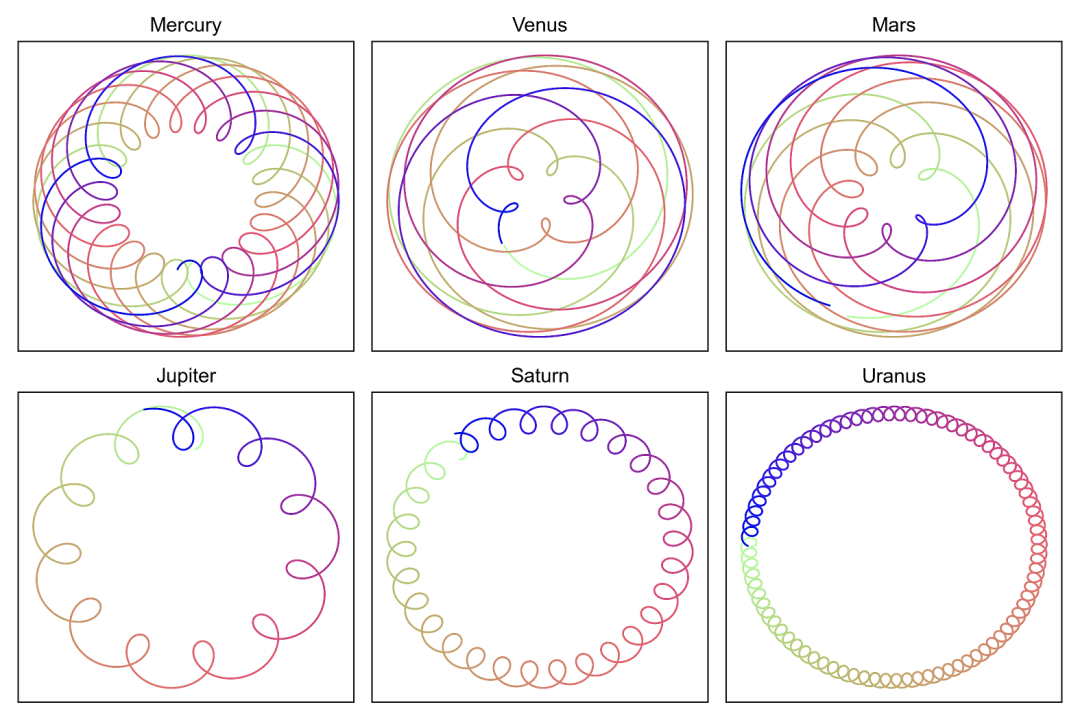
开普勒是幸运的，前有日心说，又有前辈弟谷二十多年的高质量观测数据。开普勒内心坚信日心说，但又以数据说话，并不是拍脑袋认为行星是圆周运动。他从这些复杂的运行轨迹中挖掘出了行星的轨道图形。
对的，开普勒配得上是最早一代数据挖掘大师。
他的第一定律就是椭圆轨道，第二定律是单位时间轨迹扫过面积恒定。在他关于行星运动的工作中，将椭圆的扇形面积视为线的总和，但这充其量算作一种朴素的、粗略的积分形式，开普勒并没有像希腊人那样作严谨思考。
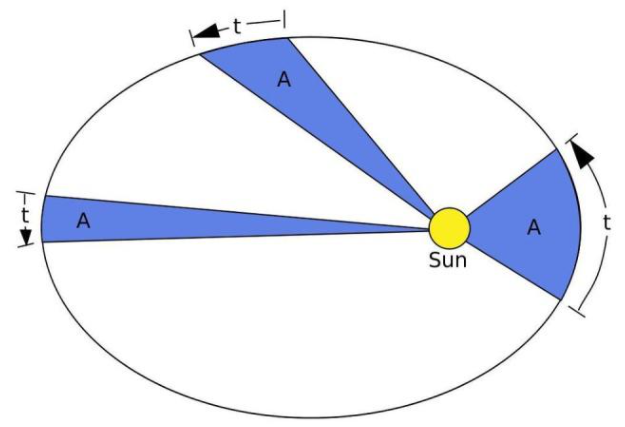
除了开普勒发现椭圆轨道外，意大利科学家伽利略（Galileo）也发现投掷物体会沿着抛物线运动。
这些在天文和力学方面的研究成果，进一步激发了人们对曲线研究的热情，代数学在这一阶段得到了极大发展。通过代数方法寻求几何问题的解决方案，成为研究曲线运动新的途径。这在一定程度上也催生了坐标几何的登场。
¸ 坐标几何
在古希腊人看来，两个数相加没什么问题，这是基本的算术运算，但一个量并不总是能加上另一个量。比如，一条线加上一个点，或者一个体积加上一个面积，是没有意义的，也就是说不该有像 这样的式子。
比如，我们用 和 分别表示两条线段的长度，那么 表示的是一个面积，此时式子 是什么意思呢? 两条线段怎么能和一个面积相加呢? 再比如，三个量的乘积 可以被称为体积，但是五个量的乘积 对应什么几何量呢?
也就是说，在他们看来只有相同类型的量才是可能相加的，而且还得对应几何量。这种对量的运算加以限制的思想，即便到了韦达那里仍然残留着。
笛卡尔的前辈，法国数学家韦达利用欧几里得的《原本》第一个提出了无穷等比数列的求和公式，发现了正切定律、正弦差公式、纯角球面三角形的余弦定理等，同时还发现了著名的韦达定理。韦达利用代数法分析几何问题的思想，正是后继者笛卡尔解析几何思想的出发点。
在笛卡尔的墓碑上刻着这样一句话：笛卡儿，欧洲文艺复兴以来，第一个为人类争取并保证理性权利的人。
为什么这么说呢？作为理性主义的代表人物，有别于经验主义者，笛卡尔坚信可以用数学撬开宇宙奥秘。在这点上，他迈出了重要的一步。
简而言之，笛卡尔通过引入单位 1，轻巧地打破了对量运算在思维上的限制。进而他引入了现在称为坐标系的思想来展示如何使用代数来解决几何问题。
笛卡尔和很多前辈一样，将代数方程不是当作纯数的运算，而是指几何量的运算，用几何术语来解释所有代数运算。
为了充分利用代数的力量，笛卡尔必须想出办法克服古希腊的思维限制，即在一定意义上必须与过去进行重大决裂。他为代数方程发明了一种新的几何解释，使代数学家摆脱了无法写出 或 等严重限制。他解放了自己，因此也解放了他的继任者，包括现在的我们。
笛卡尔选择了一条他称之为单位长度的线段，长度为 ，可以任意选择。这让他将符号 解释为一个矩形的面积，其中一条边的长度为 ，另一条边的长度为 。这样，他就可以放心地写出 ，因为它可以被认为是两个面积的总和。
更重要的是，他将乘积解释为线的长度，因此他可以将任意幂解释为线的长度。也就是说，笛卡尔的线段 和 的乘积不一定是面积 ，但可以是另一个长度，例如
并且，还可以把长度 构造出来，如下图所示。
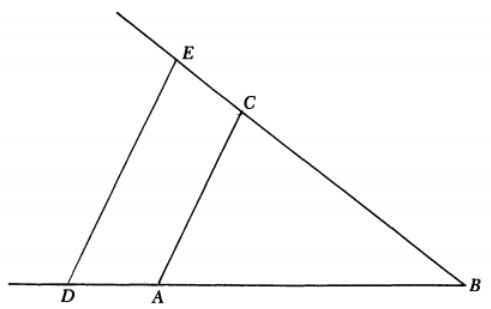
在这个例子中，给定一个单位线段 ，构造 和 的乘积。让线段 和 在起始于 的同一条线上下线，让线段 延伸并构造平行于 的 ，从而产生比例 (因为 )。因此 就是要的乘积 。
当然这是一个简单的构造，但他必须明确给出。笛卡尔的几何哲学并没有让他仅仅断言一条线段长度等于两条线段长度的乘积，他还需要构建它。
笛卡尔在他的著作《几何》中分析了当时的几何学与代数学各自的优缺点。他认为希腊人的几何过多地依赖于图形，而代数学却完全受法则和公式的限制，以至于阻碍了自由的思想和创造力。
但是，笛卡尔在《几何》中使用的潜在的坐标系中都仅有一个坐标轴是明确的。在 1649 年 Frans van Schooten 及其学生将《几何》译成拉丁文时，为阐释其中的一些想法而引入了一些概念，包括第二个坐标轴。
题外 使用字母 来表示末知量据说源于一个巧合事件。《几何》在排版时，打字员发现字母表的最后几个字母不够用了。他问笛卡儿，书中诸多方程中使用字母 还是 是否有关系。笛卡儿回答说，用哪个字母表示末知量都行。于是这个打字员就选择 ，因为字母 和 在法语中的使用频车要高于 。
3 曲线下的面积
前面说了，开普勒进一步激发了大家对曲线下的面积的计算热情。在这个问题上，三位年龄相仿的数学家相继发力，他们是意大利数学家卡瓦列里（Cavalieri，1598 - 1647）、法国业余数学家费马（Fermat，1601 - 1665）和法国数学家罗伯瓦尔（Roberval，1602 - 1675）。
开普勒对积分的尝试启发了卡瓦列里，他展示了 从 到 的积分是 ，通过计算多个 值的结果后推断出一般结果。
卡瓦列里最大的贡献是建立了祖暅原理(又名等幂等积定理，西方称为卡瓦列里原理)，依靠这个原理，他求得相当于曲线 下的面积。
此处插播一个作业，那就是需要计算如下级数，
阿拉伯数学家 Al-Haytham（965 - 1040）发现了 时的求和公式，并用它来计算抛物面的体积。
而卡瓦列里将公式推广到 ，然后猜想更一般的情况同样成立。
该公式可以用于计算某些立体的体积，甚至超越了阿基米德和开普勒的成绩。
由此还引发了以面积计算体积的方法并成为了积分发展的一个重要步骤。
罗伯瓦尔考虑了相同类型的问题，但比卡瓦列里要严格得多。
罗伯瓦尔认为曲线和直线围成的面积是由无数个无限窄的矩形条组成的。
他将这个想法应用于 ，计算从 到 的积分，声称得到近似值，
罗伯瓦尔然后断言当 趋向于无穷大时上式趋向于 ，由此算得面积。
有兴趣的不妨用下面公式验证一下上面罗伯瓦尔的结论。
比如 ，上式两边同时除以 ，得
当 取值越大，矩形就越多，它们的面积之和就越接近曲线围成的面积。
因此，当 趋向于无穷大时，上式等于 ，直觉告诉我们这就是这些矩形的面积之和，它应该也等于曲线围成的面积。
而费马的方法相对而言更加严谨一些，但同样地也没有给出相应证明。
他还推广了抛物线和双曲线，
- 从抛物线 推广到，
- 从双曲线 推广到，
¸ 切线和极值
费马不仅对解析几何有贡献，更是一位热衷于无穷小分析的好手，他大概是为了求极大、极小值问题引入了后来称为导数的概念。他写信给笛卡尔，给出了今天使用的方法，即通过计算函数的导数何时为 来找到极大值和极小值。
他认为他的求切线方法是他的求极值方法的一个应用。下图是他对抛物线上的点 求切线的做法。他令 趋于无穷小时得到切线方程。
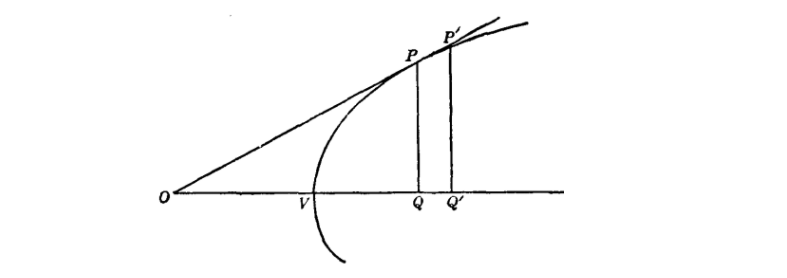
除了导数，费马也触摸到了微分与积分之间的关系，这主要源自对于曲线求长度的问题。
大概在 1660 年前不久，出现了一些曲线求长度的方法，一般是用多边形去逼近曲线，然后应用无穷小量或极限来处理的。费尔马得知这些方法以后，自己搞了一个求半立方抛物线长度的方法。他的这一做法是他的一般方法的典型，并很好地表示出他的工作中各方面的内在联系。
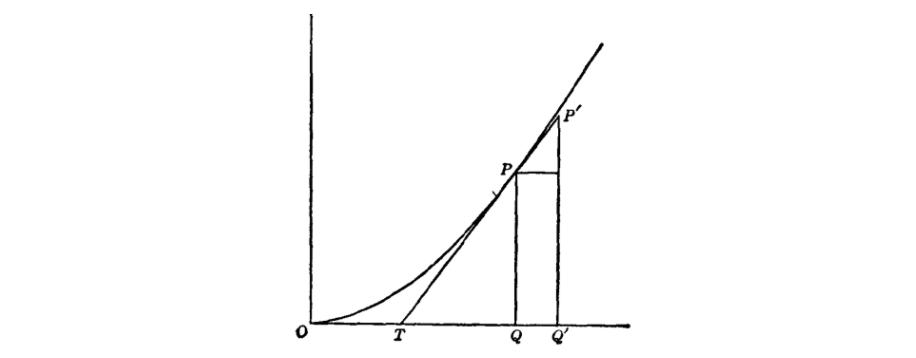
对曲线上横坐标 、纵坐标 的任一点，次切线 可以用他的切线方法求得为 。于是在离纵坐标 距离 处取切线的纵坐标 ，则线段 可以用 和 来表达。
举个具体例子，对曲线 来说，有 ，即曲线长度的增量，这个相当于后来记为 的东西。在费马看来，当 很小时， 可以看作不但在切线上，而且也在曲线上，所以曲线的长度可以视为 的线段的和。这里需要发挥一下洞察力，这些线段的和又可以作为曲线 围成的面积，用现在的写法就是，
由于这个面积已经能够求出，因此曲线长度自然也可以求得。
奇怪的是，费马用他的极大极小值方法来求重心，他将与切线有关的曲线求长问题化为一个求面积的问题，他从几何和解析的角度在各种问题上应用了无限小量，竟然会象帕斯卡一样，没有看到这两类问题之间的基本联系。
费马在这些问题中用过一些示图。这些示图和帕斯卡所用的，非常相象，这就是后来莱布尼茨感到对他的微分三角形深有启发的那张图，可是费马还没有觉察到它们的深远意义。
只要费马能对他的抛物线和双曲线求切线和求面积的结果更仔细地考察一下，他是可能会发现微积分的基本定理，并如他有时被不恰当地称呼的那样，成为微积分的真正的发明者。
费马当然在某种意义下理解到这两类问题有一个互逆关系。他之所以没有作进一步的考虑，可能是由于他以为他的工作只是求几何问题的解，而不是代表一种本身就很有意义的推理过程。
他的极大、极小值方法，切线方法以及求面积方法，在他看来是为解决这些问题而特有的方法，不是新的分析学。
此外，它们在应用上显然是有局限性的。费马只知道怎样应用它们到有理式的情况，而牛顿和莱布尼兹通过无穷级数的应用，认识到这些方法的普遍性。然而，除了巴罗以外，可能没有数学家如费马这样接近地酝酿微积分的发明。拉格朗日甚至认为费马是微积分的发明者。
4 沃利斯与《无穷算术》
笛卡尔引入坐标思想，将数和形之间被割裂的关系重新弥合起来。但他主要是打通两者，便于用代数去研究几何，并没有想将几何建立在代数的基础上。
而几何算术化的思想可以说是英国数学家沃利斯首先引入的，他用笛卡尔的坐标思想，从古希腊的截圆锥给出的定义导出方程，然后反过来用这些方程导出曲线的性质，之后完全摆脱对圆锥的依赖了。
沃利斯（Wallis，1616 - 1703）是一位对牛顿影响非常大的英国数学家。
由于他与后面牛顿等人的工作有直接关系，我们此处简述一下沃利斯的主要成就。
一般来说，沃利斯是最早把圆锥曲线当作二次曲线加以讨论的人，从此摆脱了过去将圆锥曲线视为圆锥截线的纯几何观念。
沃利斯在笛卡尔的基础上大胆引进了负的坐标值，实现圆锥曲线的算术化，对完善和传播坐标几何的思想起了重要作用。
他的《无穷算术》一书，本质上是以算术的方式大大扩展了卡瓦列里的不可分原理。
在这本书中他甚至还提出了极限的初步概念：变量的极限，是变量能如此逼近的一个常数，使它们之间的差能够小于任何给定的量。
这个定义虽然还不够严密，但却向极限的精确定义迈进了重要的一步。
牛顿曾说：大约在我的数学生涯初期，那时我们杰出的同胞沃利斯博士的著作刚刚落入我的手里，他考虑到级数，用级数插入法求出了圆与双曲线的面积。
因此，美国数学史家波耶（Boyer）说：
牛顿承认他在分析和流数方面的第一次发现，是受沃利斯的《无穷算术》的启发。
说了一堆文字，我们来看点算术化涉及到的实实在在的式子。
沃利斯推广了整数幂的运算，将指数的定义从正整数扩充至有理数，即包括 、负数以及分数。
-
，，，
-
为 的开方， 的开立方，
-
为 的开 次方。
-
为 的开 次方。
他首次引进了沿用至今的无穷大记号 。
-
沃利斯首先发表了提出抛物线、椭圆和双曲线的代数公式的工作，这是笛卡尔开创性工作的重大进展。
-
沃利斯将圆锥曲线从圆锥中解放出来的目的之一是为了寻找一种计算曲线下面积的通用方法。
他在《无穷算术》中具体讨论了这种方法。
他用代数方法计算了 的积分，即曲线 下的面积，证明这个面积是等高等底的平行四边形（未规定使用直角坐标系）的面积的 。
可以理解，他的一些结果跟别人已得出的结果是等价的。
例如，对正整数 ，可以证明当 时，有
从而得出，
沃利斯认为代数方法的简明并不逊于几何的直观，因此他更喜欢使用代数方法，并且使代数摆脱对几何的依赖。
然后更进一步，他给出了处理分数次幂的新途径，他直接去求 ，而不再像费马做过的那样去考虑曲线 。
他首先求出了 ，，，办法是考虑跟 ，， 曲线下面积互补的面积，然后通过跟已得结果得出其它分数次幂的结果。
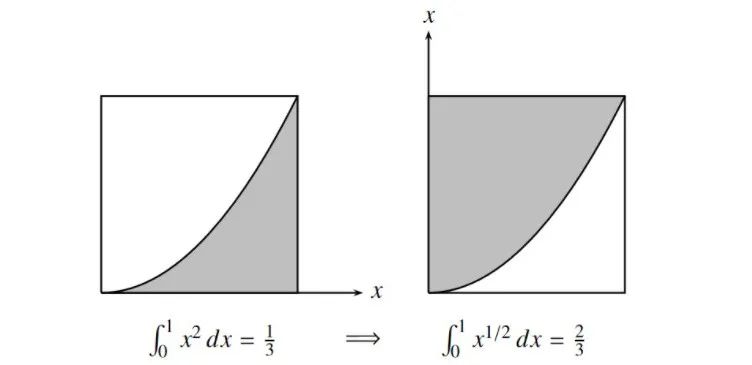
然而，有一点不得不说：沃利斯的推理按今天的标准来看，是极端不严谨的。
例如，他会根据对 观察到的一种模式，便根据归纳法宣布一个对所有正整数 均成立的公式，甚至根据插值法宣布对 为分数时也成立。
他的大胆有个好处，就是可以导出一些了不起的公式，例如他著名的无限乘积公式。
沃利斯虽然引进了分数次幂，并且计算了一些某些幂次曲线的面积，但有一条大家熟悉的曲线的面积难住了他。
那就是圆的面积，其方程为 ，因为他无法将其展开为 的幂级数。然而，他制定了插值原理。
沃利斯试图将他的方法用来计算圆的面积，即四分之一圆对应的曲线，
此时指数是分数，这其实要用到广义二项式定理，但他似乎没有考虑这个问题，因此在计算圆面积这个问题上碰到了麻烦。
然而，他发现圆 的纵坐标是曲线 和 的纵坐标的几何平均值。
这时，他想到了插值法，将 半圆的面积取为 和 的两个积分值的几何平均值，当然这只是作为近似值。
即 和 的几何平均值；这相当于将 作为 的值。
当然，沃利斯显然不满足于这样的结果。
他继续琢磨，终于想到一个法子。
牛顿极有很可能是受此方法的启发而发现了广义二项式定理，因此，我们有必要来看一看沃利斯的这个方法。
首先，沃利斯把问题统一成如下形式，
其中， 和 都是整数。
沃利斯发现上述积分总是某个整数的倒数，即 ，
例如， 和 时，有
沃利斯为了找出规律，便计算各种 的组合，并将它们的 值制成一个表。
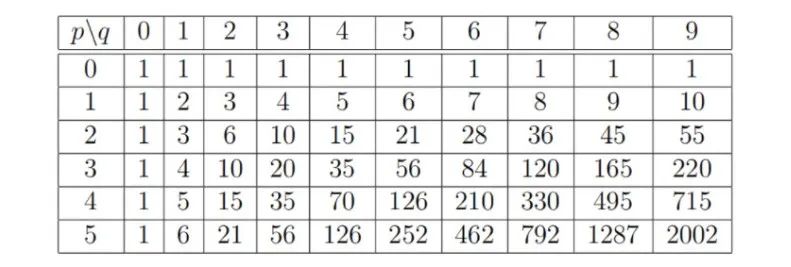
实际上，沃利斯计算了比上面更多的情况，因为他希望通过这张表发现一个用 和 表示的通用公式。
另外，他想着如果当 和 不是整数时，这个公式仍然成立的话，他可以代入 ，那岂不是可以计算想要的答案了，
理想是美好的，现实也还凑合。
他也确实发现了一些规律，那就是，
例如，在第 2 行中的值为，
以及第 3 行，
问题是沃利斯想要计算的是 ，代入前面已经发现的公式，得
这什么东东，分数的阶乘！？沃利斯那年代还没有这个玩意儿。
但作为数学家，岂能被这点事情难倒？
沃利斯自然是不畏缩的，他继续想办法制表。
什么办法呢？其实就是根据已知去猜未知，这可是有学名的，叫插值法。
我们来看看这个表，
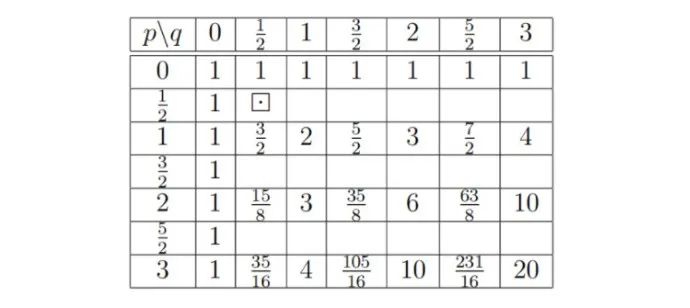
这个时候他不管三七二十一，假设 为整数，将 设为分数代入前面的式子，比如，
沃利斯在这里纯粹是试探性的，他不确定当 或 不是整数时，上述公式是否仍然对应相应的积分值。
幸运的是，他竟然猜对了，然后他得到了公式，即
简单总结就是：能算的把它们算出来，找出规律得到公式，算不了的就强行代入这个公式去算，这就算插值！
上面是一个递归公式，但至少两边对于任何数字 都是有意义的。
同样，沃利斯只知道这个公式在整数的情况下是成立的，然后他假设对于非整数也是正确的。
这样子，他就可以大胆地在任意行中向右填充。例如，在 行中，他得到
像这样继续下去，他最终完成了 那一行的值，具体如下所示,
其中，，也就是，
还记得前文说过表中这些值是积分的倒数吗？随着 的增加，积分会变小，因此这些值会变大。
于是由上面表中的最后三项可得，
将 代入，得
两边夹逼之下，随着 的增大，这个连乘积将收敛。
通过这种方式，沃利斯得到了如下令人超级吃惊的连乘公式，
好了，沃利斯的插值实验到此告一段落。
为什么要说这个事情呢？对微积分的诞生很重要吗？
也不算是，但是，可能对牛顿的影响比较大：一方面是处理分数次幂，另一方面可能也教会了牛顿去大胆地猜。
我们很快会看到，牛顿貌似也确实学到了这一招。
这么做不是简单地猜，或者说归纳。背后有我的想法，那就是对连续性的信念。自然数不是孤立的，有分数、负数，甚至有复数，我接受这些数的合法地位，因此我相信它们可以遵循同一个规律，所以我敢将它们代入同一个公式。
¸ 椭圆
最后，不知道大家有没有想过，古人是如何定义椭圆的？
首先，遗憾的是，我国古代一直没有认识到椭圆曲线。而古希腊人我们已经说过是通过截取圆锥得到的椭圆。但是椭圆轨迹的方程呢？是怎么来的呢？
我们来看一下沃利斯对椭圆的定义：
沃利斯首次采用代数语言将椭圆定义为具有性质 的平面图形，其中 为直径， 为通径（过焦点且垂直于长轴的弦长）， 为椭圆上任意一点的坐标。沃利斯的定义并没有为后人直接采用，而他为椭圆标准方程的确立开了一个头。
早在古希腊，椭圆的原始定义建立在立体图形上，需要一定的空间想象。而椭圆的平面性质，如焦半径性质已经为阿波罗尼斯所发现，但直到 17 世纪，人们才逐渐摒弃椭圆的原始定义，历史同样惊人地跨越了漫长的两千年！
尽管古希腊人已经将圆锥曲线看作轨迹，但在坐标几何诞生之前，将曲线看成轨迹并不是研究曲线性质的前提，人们似乎并不需要采用新定义。只有在坐标几何诞生之后，需要将曲线看作动点的轨迹以建立其方程，或根据方程研究曲线的性质，而不再依赖几何语言和几何方法。
最后再提一下，在当时以及包括后来的牛顿莱布尼兹时代，对数学（特别是分析）的论证远没有那么严谨。我们将很快见识到牛顿沿着沃利斯的步法叩开微积分大门。
休息一下，未完待续