机器学习最全知识点汇总
点击下方卡片,关注“新机器视觉”公众号
重磅干货,第一时间送达

1.列举常用的最优化方法
梯度下降法
牛顿法,
拟牛顿法
坐标下降法
梯度下降法的改进型如AdaDelta,AdaGrad,Adam,NAG等。
2.梯度下降法的关键点
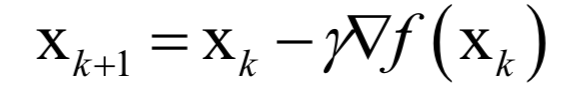
3.牛顿法的关键点
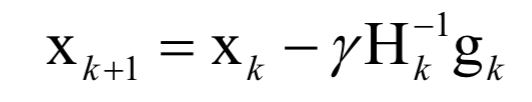
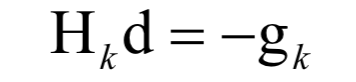
4.拉格朗日乘数法
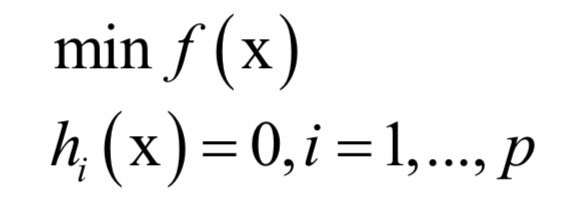

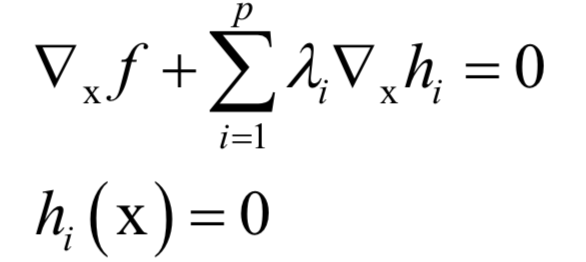
主成分分析
线性判别分析
流形学习中的拉普拉斯特征映射
隐马尔科夫模型
5.凸优化
优化变量的可行域是一个凸集
目标函数是一个凸函数
线性回归
岭回归
LASSO回归
Logistic回归
支持向量机
Softamx回归
6.拉格朗日对偶
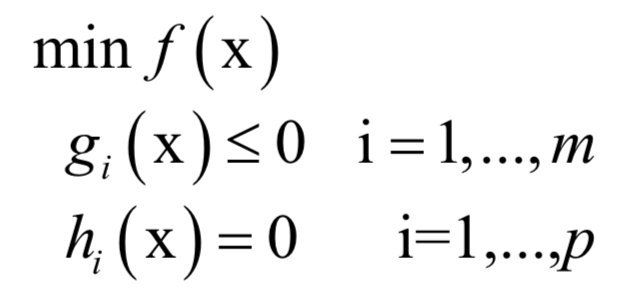
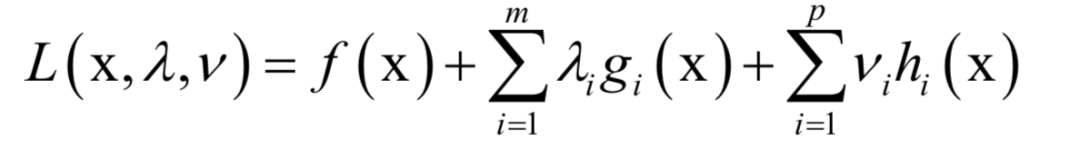
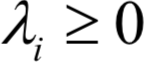 的约束。原问题为:
的约束。原问题为: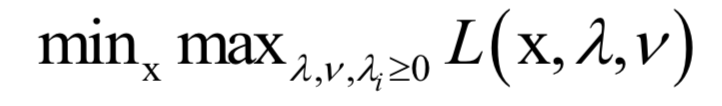
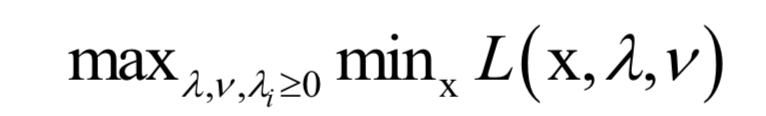
7.KKT条件
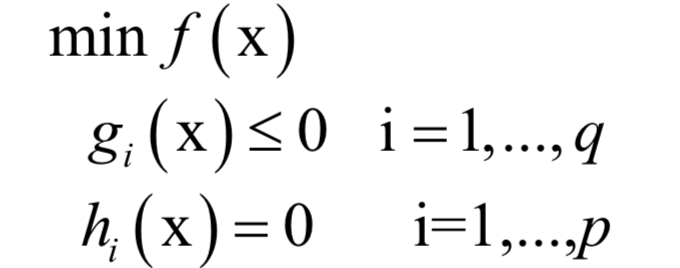

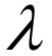 和
和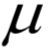 称为KKT乘子。在最优解处
称为KKT乘子。在最优解处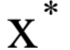 应该满足如下条件:
应该满足如下条件:
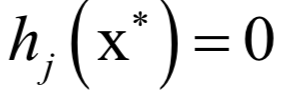
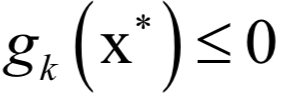
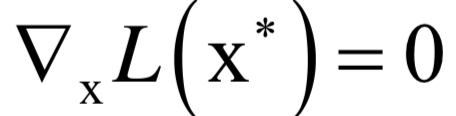 和之前的拉格朗日乘数法一样。唯一多了关于gi (x)的条件:
和之前的拉格朗日乘数法一样。唯一多了关于gi (x)的条件: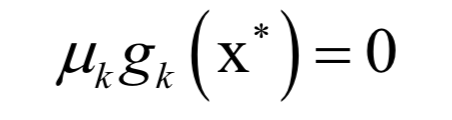
8.特征值与特征向量
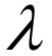 和一个非0向量X,满足:
和一个非0向量X,满足: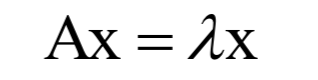
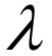 为矩阵A的特征值,X为该特征值对应的特征向量。根据上面的定义有下面线性方程组
为矩阵A的特征值,X为该特征值对应的特征向量。根据上面的定义有下面线性方程组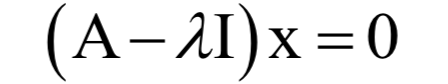
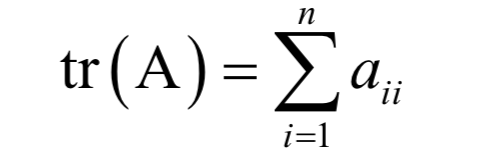
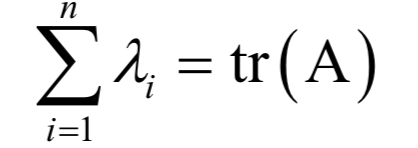
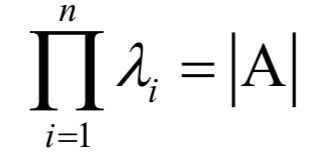
9.奇异值分解
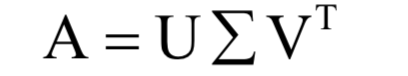
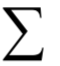 为m x n的对角矩阵,除了主对角线
为m x n的对角矩阵,除了主对角线10.最大似然估计
 ,确定这些参数常用的一种方法是最大似然估计。
,确定这些参数常用的一种方法是最大似然估计。 。最大似然估计的直观解释是,寻求一组参数,使得给定的样本集出现的概率最大。
。最大似然估计的直观解释是,寻求一组参数,使得给定的样本集出现的概率最大。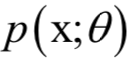 ,其中X为随机变量,
,其中X为随机变量, 为要估计的参数。给定一组样本xi,i =1,...,l,它们都服从这种分布,并且相互独立。最大似然估计构造如下似然函数:
为要估计的参数。给定一组样本xi,i =1,...,l,它们都服从这种分布,并且相互独立。最大似然估计构造如下似然函数: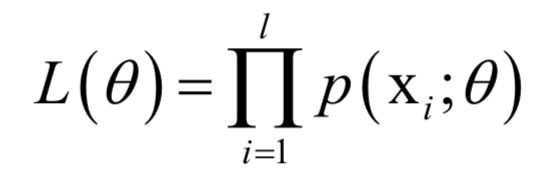
 的函数,我们要让该函数的值最大化,这样做的依据是这组样本发生了,因此应该最大化它们发生的概率,即似然函数。这就是求解如下最优化问题:
的函数,我们要让该函数的值最大化,这样做的依据是这组样本发生了,因此应该最大化它们发生的概率,即似然函数。这就是求解如下最优化问题:
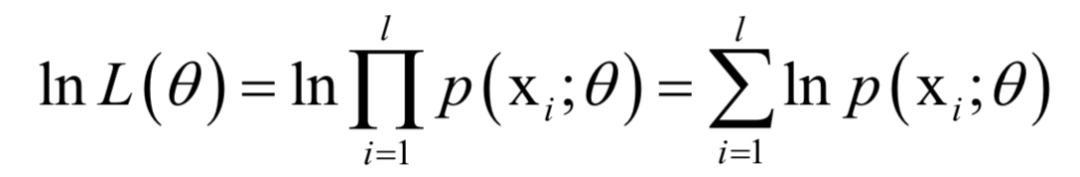
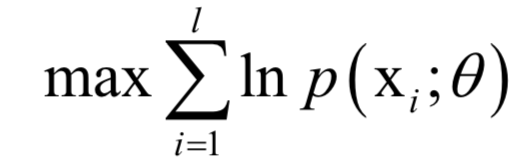
基本概念
1.有监督学习与无监督学习
2.分类问题与回归问题
3.生成模型与判别模型
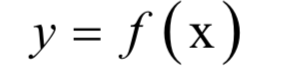
4.交叉验证
5.过拟合与欠拟合
6.偏差与方差分解
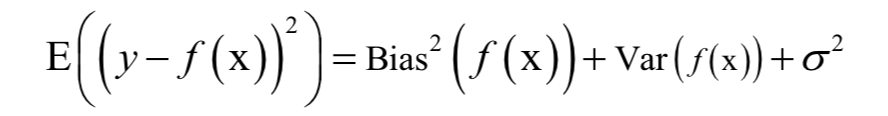
7.正则化
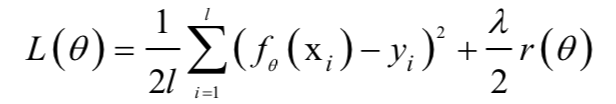
8.维数灾难
贝叶斯分类器
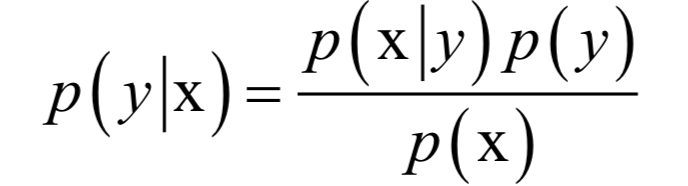
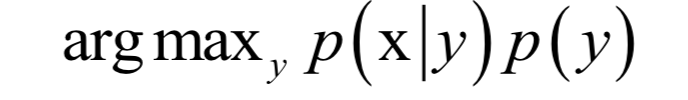
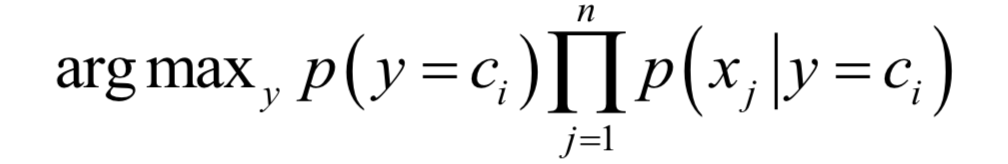
决策树
1.用样本集D建立根节点,找到一个判定规则,将样本集分裂成D1和D2两部分,同时为根节点设置判定规则。
2.用样本集D1递归建立左子树。
3.用样本集D2递归建立右子树。
4.如果不能再进行分裂,则把节点标记为叶子节点,同时为它赋值。
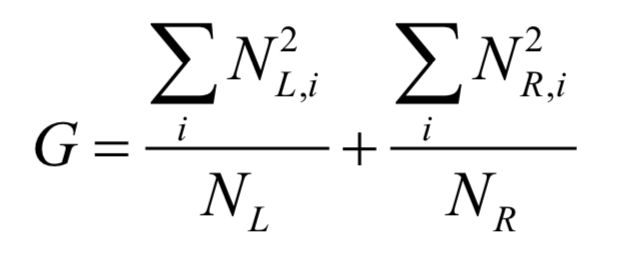
随机森林
AdaBoost算法
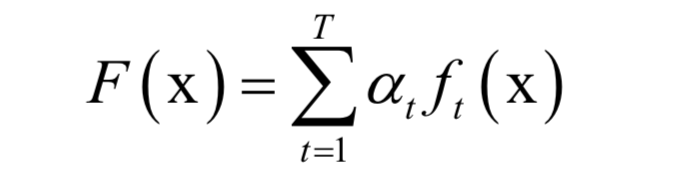


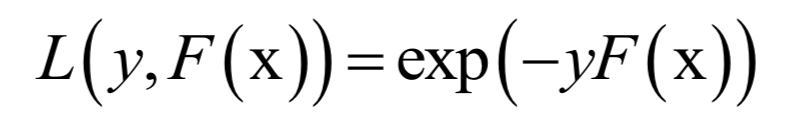
主成分分析

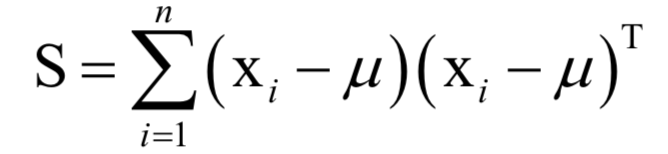
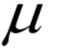 为所有样本的均值向量。则上面的重构误差最小化等价于求解如下问题:
为所有样本的均值向量。则上面的重构误差最小化等价于求解如下问题: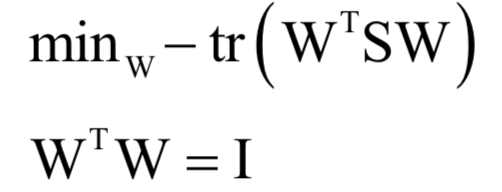
线性判别分析
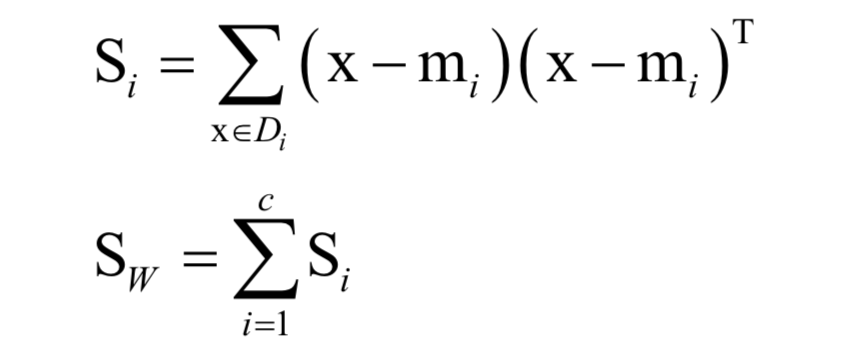
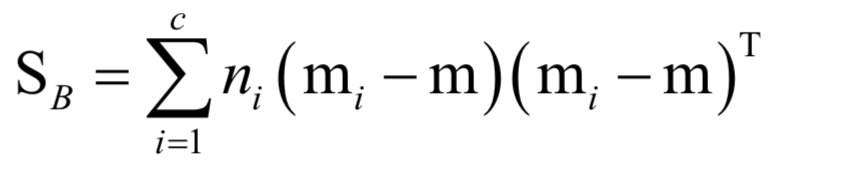
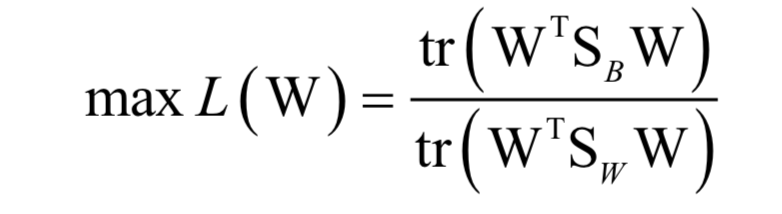
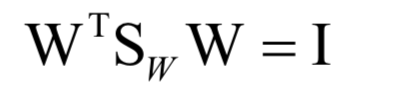
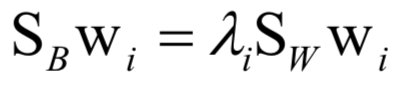
kNN算法
人工神经网络

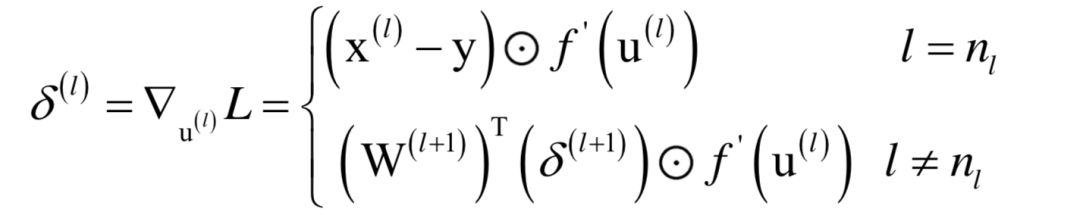
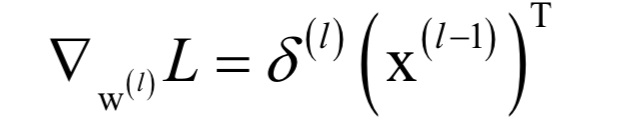
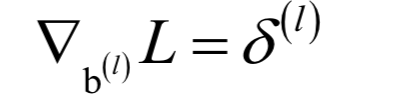
支持向量机


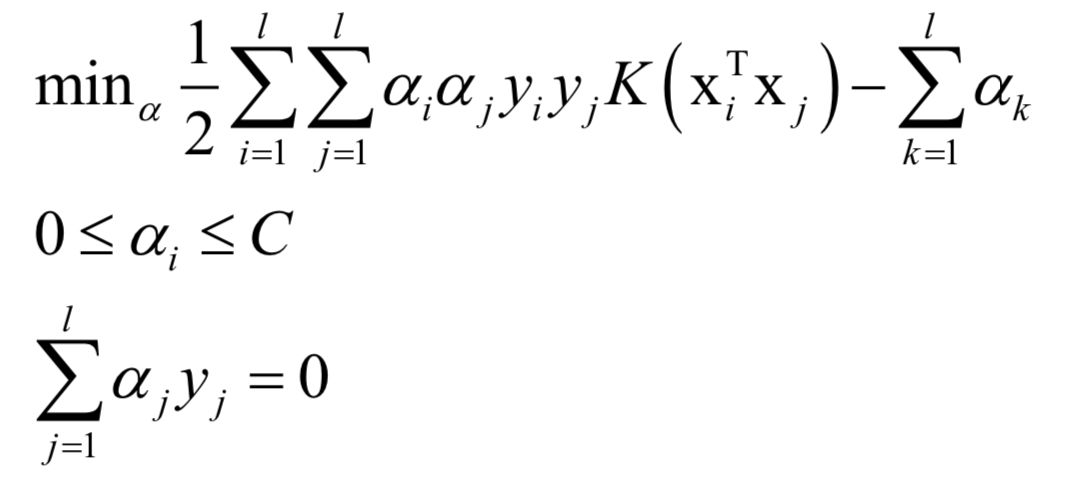

logistic回归
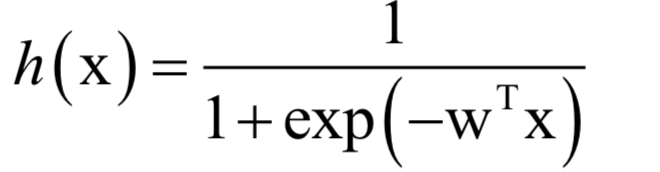
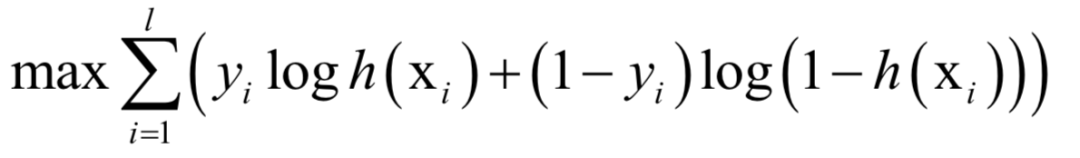
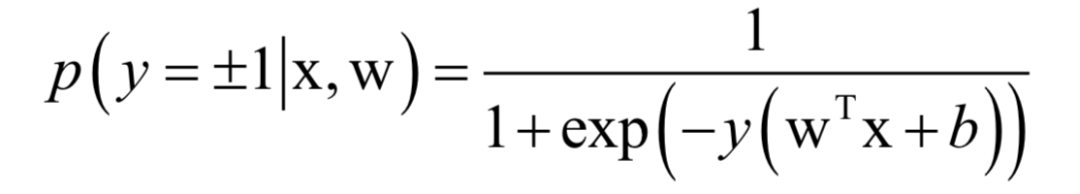

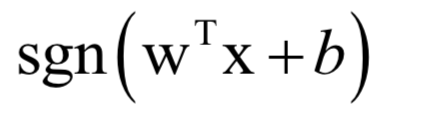
K均值算法
卷积神经网络
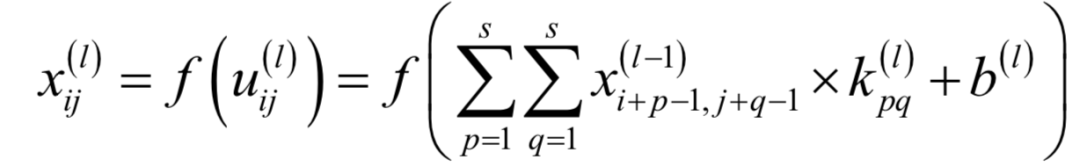
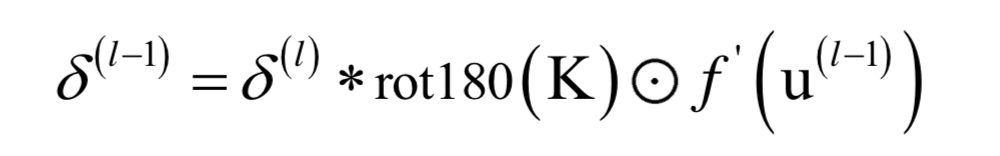
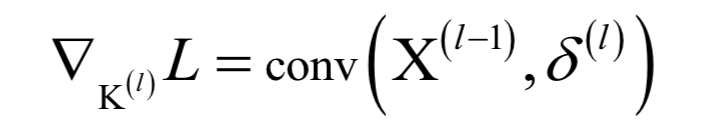
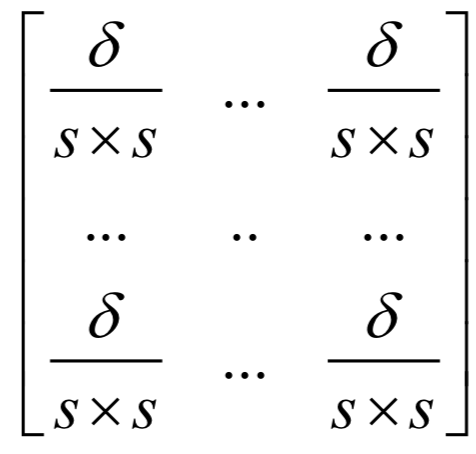
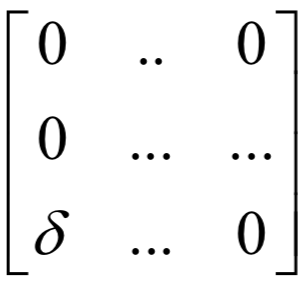
循环神经网络
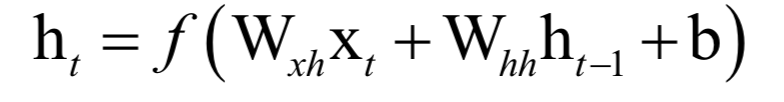
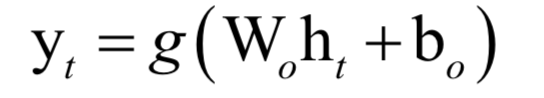
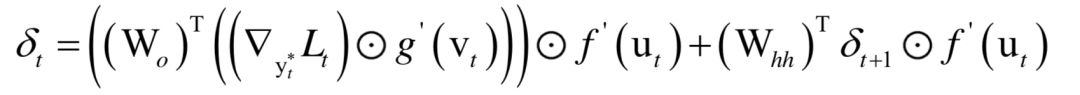
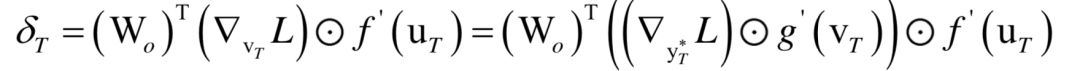
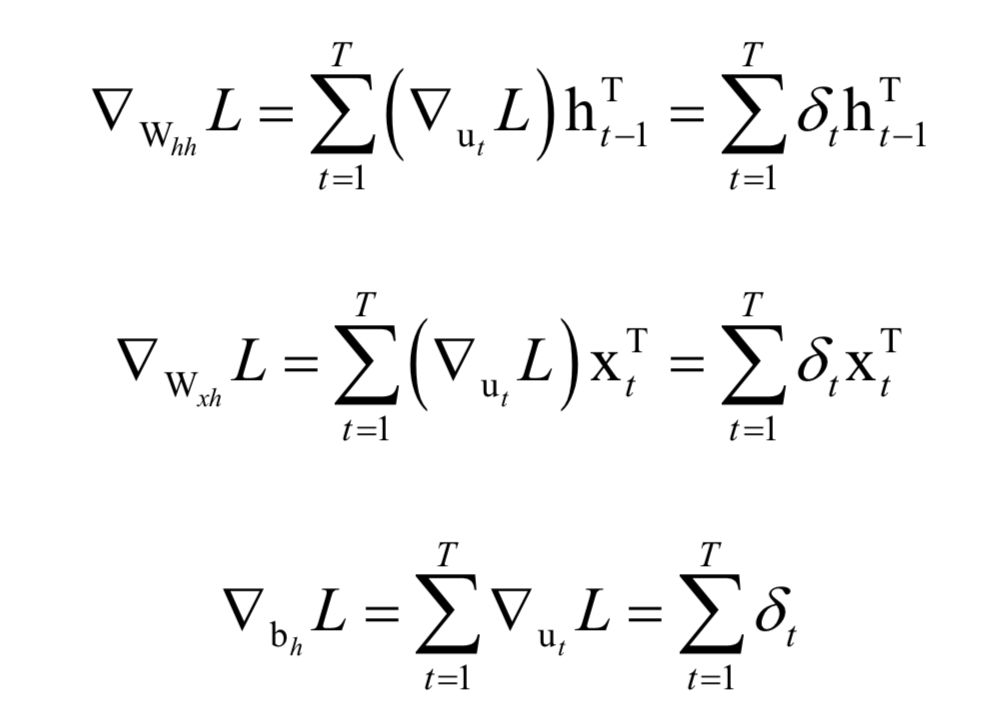
高斯混合模型
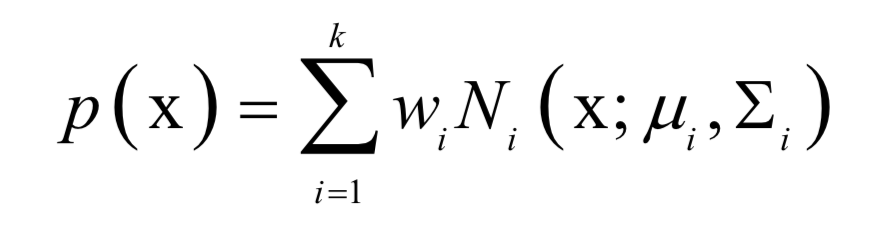
 为高斯分布的均值向量,
为高斯分布的均值向量,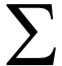 为协方差矩阵。所有权重之和为1,即:
为协方差矩阵。所有权重之和为1,即: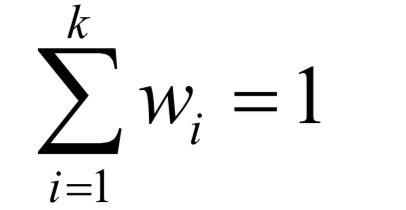
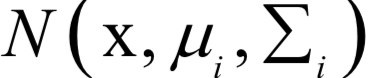 产生出这个样本数据x。高斯混合模型可以逼近任何一个连续的概率分布,因此它可以看做是连续性概率分布的万能逼近器。之所有要保证权重的和为1,是因为概率密度函数必须满足在
产生出这个样本数据x。高斯混合模型可以逼近任何一个连续的概率分布,因此它可以看做是连续性概率分布的万能逼近器。之所有要保证权重的和为1,是因为概率密度函数必须满足在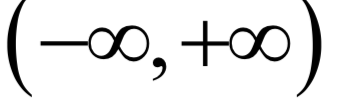 内的积分值为1。
内的积分值为1。EM算法
 的值,接下来循环迭代,每次迭代时分为两步:
的值,接下来循环迭代,每次迭代时分为两步: ,计算在给定x时对z的条件概率的数学期望:
,计算在给定x时对z的条件概率的数学期望:
 的值:
的值: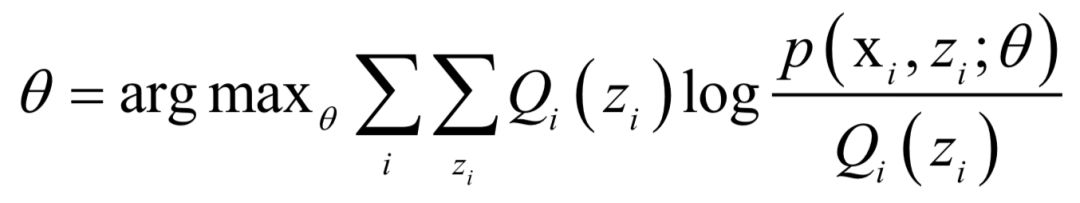

本文仅做学术分享,如有侵权,请联系删文。
评论
