机器学习所需要的线性代数学习知识攻略(内附机器学习路径图)

我为什么推荐这个专栏?
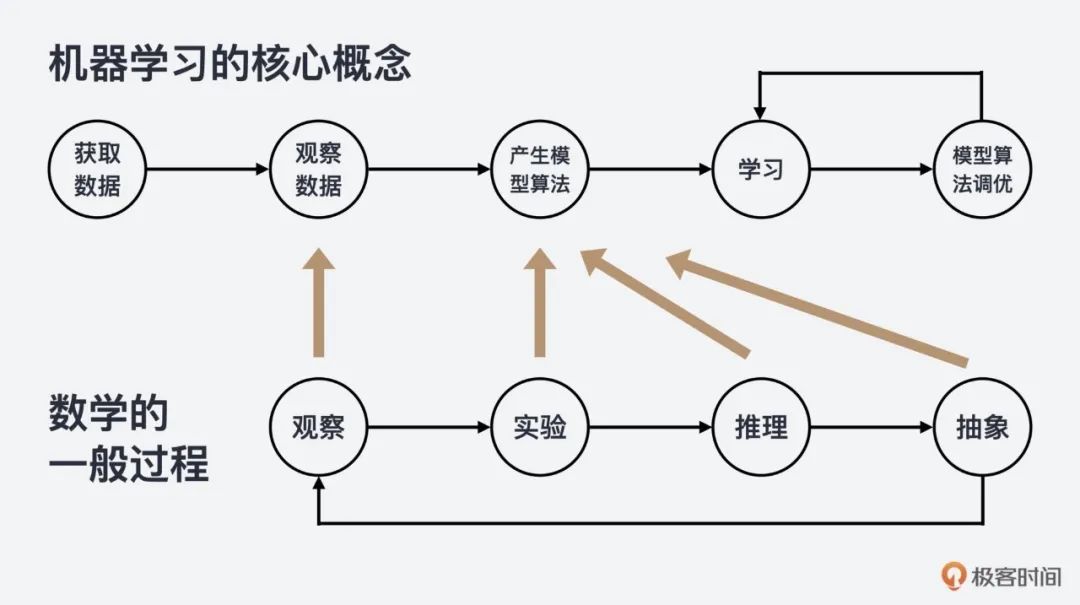
先从最简单的线性方程组说起,在这基础上引出向量和矩阵,并通过矩阵来解线性方程组的不同方法。
然后,在向量和矩阵的基础上讲线性空间,因为在实践中,更多的是对集合的操作,也就是对线性空间的操作。线性空间好比是容器,它包含了向量,以及向量的运算。
最后,介绍解析几何,是解析几何使得向量从抽象走向了具象,让向量具有了几何的含义,比如:计算向量的长度、之间的距离和角度,这在机器学习的主成分分析PCA中是非常有用的。
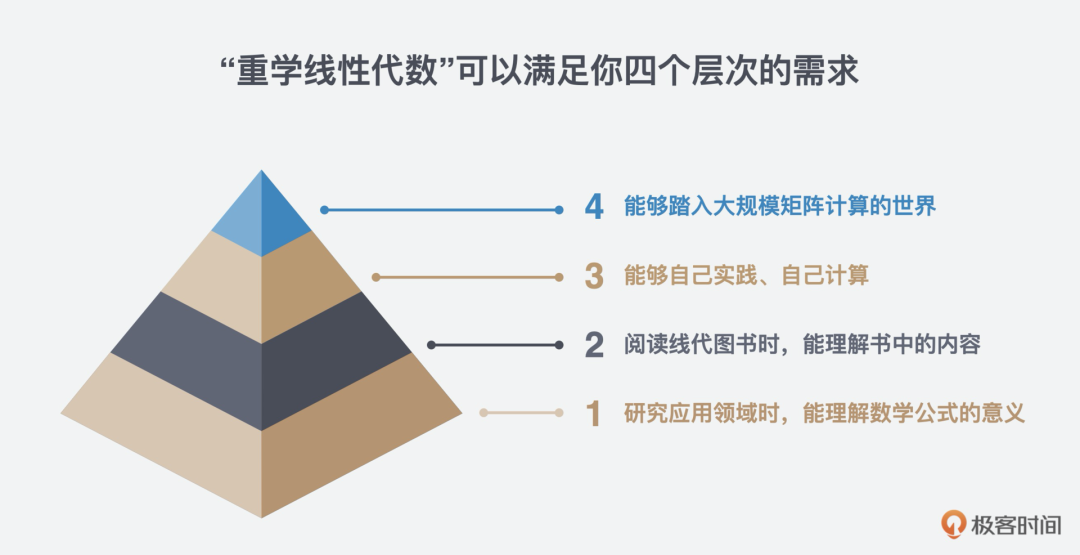
第一层次:在研究应用领域时,希望能够理解数学公式的意义。 第二层次:在阅读线性代数参考书时,希望理解书中的内容。 第三层次:能够自己实践、自己计算。 第四层次:能够踏入大规模矩阵计算的世界。

评论
