抛弃P值，选择更直观的A/B测试！

大家好，我是宝器！

在两个选项中做出选择，该如何选？一个简单而又智能的方法就是A/B。本篇文章将简要地解释A/B测试背后的动机，并概述其背后的逻辑，以及带来的问题：它使用的P值很容易被误解。

因此，本文用贝叶斯魔法来完善这种方法，讲讲什么是贝叶斯A/B测试，一个不需要P值的A/B测试。

A/B测试的动机

想象一下，你经营着一个比较成功的网上商店，每天有大约10,000名访客。在这一万人中，约有100人真正从你的商店买了东西——你所谓的转化率约为100/10,000=1%，这相当小。（大多数网上商店实现的转换率约为1-3%，亚马逊甚至超过10%）

由于很多人都到过你的商店，但其中只有极少数人成为顾客，因此你的结论是提高商店的转换率，因为这是提高收入的最大杠杆。

到底是什么让人们不买我的好产品呢？

你想不出一个好的解释，所以你向一些朋友寻求灵感。他们告诉你，他们不喜欢你的购买按钮的蓝色。也许红色会更吸引访客？可以用数据说话！

开始战斗吧! 其方法如下：

以50%的概率将新访客随机分配到蓝队或红队。蓝队的人将看到蓝色按钮，红队的人看到红色按钮。在这个过程运行一段时间后，你可以检查哪个团队的转换率更高。

说明：称蓝队为对照组，红队为测试组。对照组给你一个指示，如果你让一切保持原样会发生什么，测试组告诉你如果你做某种干预，例如改变按钮的颜色会发生什么。

请注意，如果你想轻松地评估实验，这种随机化很重要。你不应该做的事情包括：

• 将所有男性分配到红色团队，所有女性分配到蓝色团队。即使一个团队的转换率再高，你也无法知道这是否是由于按钮的颜色或仅仅是性别的原因。
• 这周把所有人分配到红色团队，下周分配到蓝色团队。即使一个团队的转换率高得多，你也无法知道这是否是由于按钮的颜色，或者人们只是在一周内买了更多的东西，不管是什么颜色。也许其中一个星期包括像黑色星期五或圣诞节这样的节日，或者其他更微妙的季节性模式。

为了提炼出按钮颜色效应，不应该有其他的混淆效应，能够解释两队的不同转换率也是如此。

准备A/B测试

不妨假设A/B测试已经进行了一天的适当的数据收集，最后得到了一些数据。你有正好10,000名访客，你将其随机分组为蓝色组（对照组）和红色组（测试组）。你记录了这个访客是否买了东西（编码为 1 ）或没有（编码为 0 ）。

我们可以用以下代码来模拟结果：

import numpy as np
np.random.seed(0)
blue_conversions = np.random.binomial(1, 0.01, size=4800)
red_conversions = np.random.binomial(1, 0.012, size=5200)

你可以看到，我把1%作为对照组的转换率，1.2%作为测试组的转换率。所以你已经知道，如果抽样没有做什么太奇怪的事情，红色按钮应该表现得更好！这就是为什么我们要把数据放在对照组中。但从现在开始，假设数据的产生是未知的，因为这就是我们在现实中一直面对的情况。

请注意：这些小组有不同的规模，这通常发生在随机分配中。他们大约是10,000/2=5,000人，但不太可能得到如此完美的50:50比例。

两个NumPy数组都由1和0组成，大部分元素为0。

print(blue_conversions)
# output: [0 0 0 ... 0 0 0]
print(red_conversions)
# output: [0 0 0 ... 0 0 0]

我们可以检查的下一件事是访问者（即购买某物的访问者）的份额。

print(f'Blue: {blue_conversions.mean():.3%}')
print(f'Red: {red_conversions.mean():.3%}')
# output: Blue: 0.854%, Red: 1.135%

这表明红色按钮的性能可能更好，但目前我们还不能确定。即使不同组的转化率完全相同，一个组最终的转化率也会高于另一组的转化率很高。

我们必须排除这仅仅是偶然发生的，而这正是 A/B 测试的目的。

进行A/B测试

现在让我们看看如何更好地解释正在发生的事情。蓝色按钮还是红色按钮更好？首先，我们将以传统的方式再现，之后，我们将以贝叶斯的方式进行。

传统方式

我不会在这里深入，因为有很多资源可以完美地解释如何进行正常的 A/B 测试。你想知道以下两个假设中的哪一个是正确的：

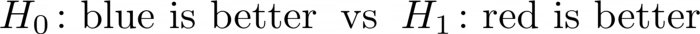
基本上，你计算某种测试统计数据，如Fisher's exact test或Welch's t-test 。然后计算一个 p 值并检查它是否在某个任意范围内，如5%。不妨选择Welch-t检验。

from scipy.stats import ttest_ind
print(f'p-value: {ttest_ind(blue_conversions, red_conversions, equal_var=False, alternative="less").pvalue:.1%}')
# output: p-value: 7.8%

因为有些人对P值很纠结，这里解读下它：

鉴于H₀是正确的，我们得到所观察到的或更极端的结果的机会最多是7.8%。

由于 7.8% > 5%，我们保留原假设。红色按钮是否明显好并不明确，所以我们只留下蓝色按钮。

我认为 p 值的定义相当不直观——每个误解 p 值的人都证明了这一点。最常见的误解如下：

蓝色更好的概率是 7.8%。（错误的！！！）

虽然没人说过要这么理解，但做出这么清晰而简洁的描述看起来也没什么毛病，不是吗？现在，贝叶斯来拯救 A/B 测试。

贝叶斯A/B测试的优点

贝叶斯 A/B 测试具有以下优点：

1. 它使你能够以一定的概率作出关于一个版本比另一个版本更好的声明。这正是我们想要的。
2. 你不需要知道所有的统计测试。你只需建立一个适当的生成模型并按下贝叶斯推断按钮。

假设你现在已经有一些关于使用PyMC3的知识，没有的话，请查看上面链接的文章。

为了更清楚地说明这些优点，让我们在PyMC3的帮助下用贝叶斯的方式分析我们的问题。首先，我们需要考虑需要推断哪些参数。这很容易，有两个未知参数：

• 蓝色按钮的转换率；
• 红色按钮的转换率。

我们现在需要决定两个参数的先验分布。由于转化率可能介于 0 和 1 之间，因此Beta分布是有意义的。Beta 分布有两个参数 a 和 b，可以通过改变它们来创建不同的分布。

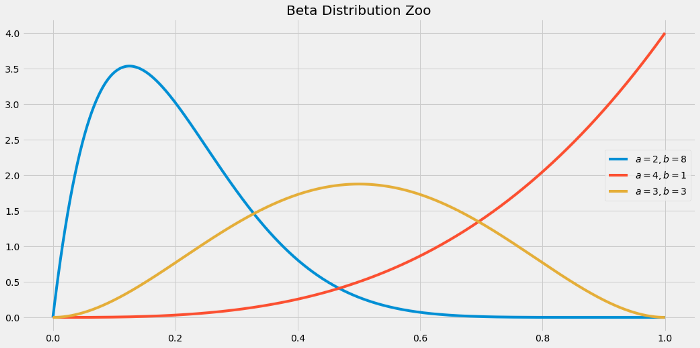
因为我们知道转化率相当小，所以它们的良好先验是 Beta(1, 99)。

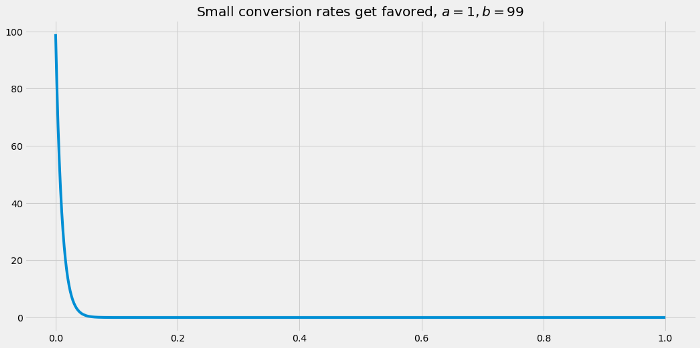
现在，我们必须考虑如何将观察到的结果（包含0和1的数组）与这些参数联系起来进行建模。直接的方法是使用伯努利变量（Bernoulli_distribution），因为它们可以只取0和1的值，并使用一个概率参数。

长话短说，我们可以编写以下程序：

import pymc3 as pm

with pm.Model():
    blue_rate = pm.Beta('blue_rate', 1, 99)
    red_rate = pm.Beta('red_rate', 1, 99)
    
    blue_obs = pm.Bernoulli('blue_obs', blue_rate, observed=blue_conversions)
    red_obs = pm.Bernoulli('red_obs', red_rate, observed=red_conversions)
    
    trace = pm.sample(return_inferencedata=True)

加上这些解释，这个程序对你来说应该是有意义的。在模型的前两行，我们定义了先验参数。之后，我们设计了模型的输出（伯努利变量），并使用 "observed "参数给它提供了A/B测试准备中的观察结果。最后一行是著名的贝叶斯推理按钮的PyMC3版本。

在trace对象的帮助下，你可以重建转换率的后验分布。

import arviz as az
az.plot_posterior(trace)

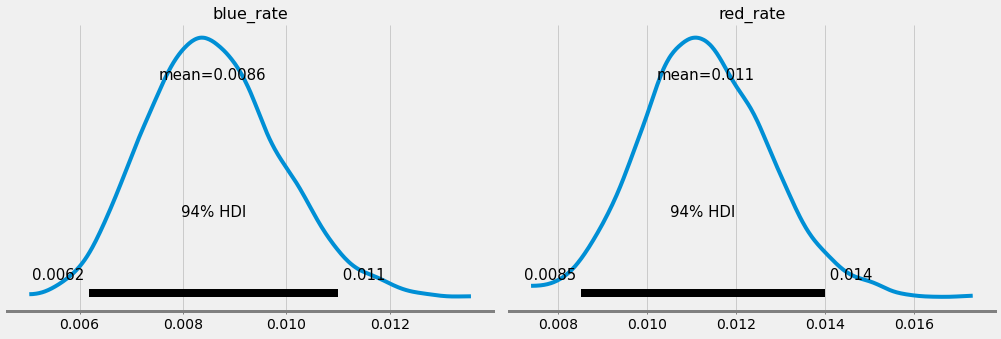
我们发现最大可能性估计转换率，蓝色约为0.854%，红色约为1.135%，甚至还有这些估计值的可信区间。例如，蓝色的比率在0.62%和1.1%之间，概率为94%。

很好，对吗？但这并没有回答我们的问题。红色按钮的转换率比蓝色按钮的转换率高的概率是多少？要回答这个问题，我们可以对两个后验分布进行抽样，看看红色比率比蓝色比率高的频率。幸运的是，这些样本已经存储在trace对象中。我们只需要看看红色比率样本比蓝色比率样本大的频率。

blue_rate_samples = trace.posterior['blue_rate'].values
red_rate_samples = trace.posterior['red_rate'].values

print(f'Probability that red is better: {(red_rate_samples > blue_rate_samples).mean():.1%}.')
# output (for me): Probability that red is better: 91.7%.

这是我们可以使用的东西！这对我们来说很容易，但其他人——我特别希望业务部门——都能理解。红色按钮更好，概率在 92% 左右？

“完美！”，可以选择店里的红色版本能够提高你的转化率！

现在想象一下：这只是一个有可能增加销售额的微小变化。可能还有其他各种更小和更大的东西可以修补，让你的商店变得更好。比赛才刚刚开始！

结论

有很多情况下，我们必须在两个选项中做出选择。这可以是一个按钮的颜色，也可以是网站上一个物体的位置，一个按钮或图片上的文字，任何有可能被改变的东西。

在两个版本中进行选择的一种方法是进行A/B测试。这个想法很简单。你可以把客户分成两组，这两组只在你想要更改的方面有所不同，即一个按钮的颜色。这样你就可以确定只有你改变的东西导致了结果的改变，而不是其他任何东西。不是人们的年龄或性别，也不是你收集数据的工作日。

通常情况下，人们使用经典的 A/B 测试，往往会使用 p 值。虽然这是统计学家熟悉的概念，但普通人经常会得到涉及 p 值的混淆陈述。这就是我们转向贝叶斯 A/B 测试的原因，它允许每个人都能轻松掌握结果。最后，我们甚至可以用 PyMC3 制定这样的结果，而不需要太多的代码。

原文链接🔗：

https://towardsdatascience.com/bayesian-a-b-testing-in-pymc3-54dceb87af74