经典算法回顾 - 快速 get 核-PCA 的要点

引言

在机器学习中，将数据点按行摆放，所有数据点就构成一个矩阵（也可以看成表格、二维数组）。矩阵的一行对应一个数据，矩阵的一列对应一个特征，因此也称为特征矩阵。如下图所示，用矩阵 表示一个具有 个数据和 个特征的数据集，

对于已经零中心化（即 ）的 个数据 （），其中每个数据都有 个特征，即 。而主成分分析（PCA）可以看作一种对协方差矩阵进行对角化的方法。那么有必要看一下协方差矩阵的定义。

上面矩阵的元素对应特征之间的协方差，这种定义形式简单也好理解。

以上是在原始特征空间中作主成分分析，但本篇的主题是核主成分分析。所谓核，则是为在更高维的特征空间作分析服务的。首先，假设我们通过以下方式将数据非线性映射到特征空间 中，

为什么要将数据映射到更高维空间中呢，不是增加了计算量吗？主要目的是想让数据在更高维空间中线性可分。因为拿一个超平面将数据一分为二是行走江湖的基本招术。记住，机器学习的一个基本招术 - 劈柴功。

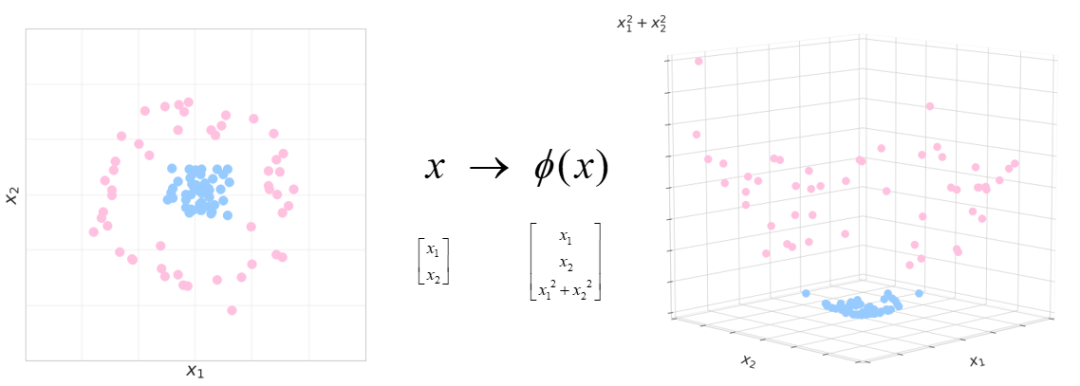
这个简单例子中，仅仅对数据增加一个维度即可，在三维空间中就可以施展劈柴大功将两类轻松分开。

我们回到核 PCA，可以证明，即使 具有任意大的维度，对于 的某些选择，我们仍然可以在 中执行 PCA。

但这里我们需要解决一个问题，那就是我们并不知道映射函数 ，那么如何在高维空间中执行 PCA 呢？这可以进一步分为两个问题，

• 一个是如何计算新特征的协方差矩阵；

• 另一个在高维空间中往新坐标轴投影得到新的坐标。

答案是，并不需要直接计算这些值，而是通过使用所谓的核技巧来实现的。下面就来看这是如何推导出来的。

核 PCA

假设将数据映射到新的特征空间中，并且 ，， 也已零中心化，即 。要在映射后的高维空间作 PCA 的话，先要求协方差矩阵，但我们会发现此时无法用式 (1) 来计算，因为我们并不知道 长啥样，从而也就不知道映射到高维空间后的新特征。

换句话说，我们只知道目标是将数据映射到更高维的空间中去，但并不给出怎么映射过去。那么问题来了，如何在高维空间中计算相应的协方差矩阵呢？类似于矩阵奇异值分解的秩-1 展开式，协方差矩阵也可以写为另一种形式，即展开为 个秩-1 矩阵之和，可以将式 (1) 改写为如下形式，

对照式 (1) 和式 (2)，会发现它们其实是同一个协方差矩阵的两种表示形式。回到核问题，此时将高维空间中的点代入，得

同样的，我们不知道映射函数 啊，怎么计算上式呢？其实呢，我们并不需要显式计算它，而最终只需要知道新特征的内积即可。我们先不纠结于此，继续往下看。

回顾一下 PCA（可以看这篇），我们需要找到满足 的特征值 和特征向量 。将式 (3) 代入，得

仔细一看，发现所有解 都位于新特征

张成的空间内。即存在系数 使得

从 PCA 方法那里可知，我们只需要知道上式中的系数就知道了所谓的主方向 PC。因此，问题转化为如何求解这些系数 。

我们可以考虑一个等价系统，即对于所有 ，计算

将式 (3) 和式 (4) 代入式 (5)，将出现我们真正需要计算的新特征间的内积，即 。

接下来，我们如下定义一个 矩阵 

由上面两式可得，

其中 表示 组成的列向量。为了求解式 (7)，我们计算如下方程的对应非零特征值的特征向量

显然，式 (8) 的所有解都满足式 (7)。

如果对解 施加向量归一化要求（即 ），可借助式子 (5)，(6) 和 (8)，因此转化为一个二次型

而对于投影到主成分，我们可以根据以下公式计算测试点 的映射 到 中的特征向量 的投影，

到此，第二个问题，即在高维空间中的投影问题也被搞定了。

注意，式 (6) 和式 (10) 都不需要提供映射函数 ，仅需内积即可。

因此，我们能够使用核函数来模拟这些内积，而无需给出实际的映射函数。常用的核函数有多项式核，

径向基核

以及 sigmoid 核

等等。可以证明，次数为 的多项式核对应于映射的 进入一个特征空间，该特征空间由输入模式的 项的所有乘积构成，例如，对于 ，有

小结

不知道映射函数 ，更不知道新特征 ，如何在高维特征空间中执行 PCA 呢？

仔细一想，在高维特征空间中计算协方差矩阵也好，投影到主成分也好，其实都是以内积的形式出现的。

因此，完全可以绕过对映射函数的依赖，直接用某些核函数来模拟高维空间中向量的内积来间接执行 PCA。当然，这个内积的效果好不好，也只有试了才知道。

附录

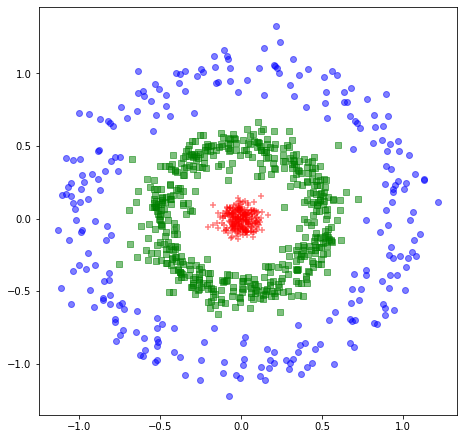
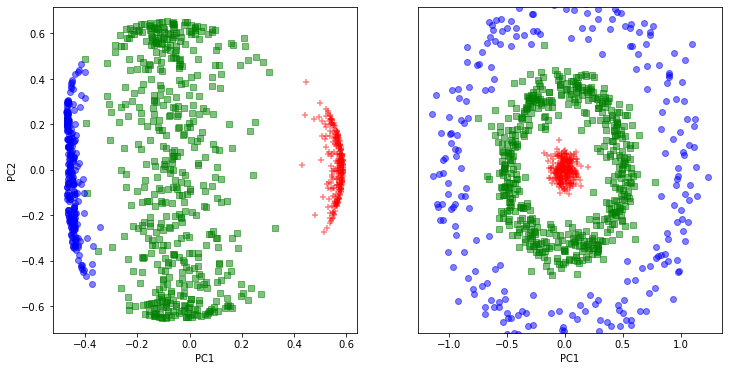
最后，来一个小例子快速实验一下，我们使用 sklearn.decomposition 实现好的版本分别采用 rbf 核和多项式核来对三个同心圆数据执行 KPCA，发现这个例子中 rbf 的效果优于多项式核。

X1, y1 = make_circles(n_samples=500, random_state=123, noise=0.1, factor=0.1)X1 = X1*0.5

X2, y2 = make_circles(n_samples=500, random_state=123, noise=0.1, factor=0.5)

X = np.r_[X1, X2]

y = np.r_[1-y1, 2-y2]

plt.figure(figsize=(7.5,7.5))plt.scatter(X[y==0, 0], X[y==0, 1], color='red', marker='+', alpha=0.5)plt.scatter(X[y==1, 0], X[y==1, 1], color='green', marker='s', alpha=0.5)plt.scatter(X[y==2, 0], X[y==2, 1], color='blue', marker='o', alpha=0.5)plt.show()

from sklearn.decomposition import KernelPCAkpca_0 = KernelPCA(kernel='rbf',fit_inverse_transform=True,gamma=3.5)X_kpca_0 = kpca_0.fit_transform(X)
kpca_1 = KernelPCA(kernel='poly',degree=1,fit_inverse_transform=True,gamma=1.0)X_kpca_1 = kpca_1.fit_transform(X)

fig, ax = plt.subplots(nrows=1,ncols=2, figsize=(12,6))ax[0].scatter(X_kpca_0[y==0, 0], X_kpca_0[y==0, 1],               color='red', marker='+', alpha=0.5)ax[0].scatter(X_kpca_0[y==1, 0], X_kpca_0[y==1, 1],              color='green', marker='s', alpha=0.5)ax[0].scatter(X_kpca_0[y==2, 0], X_kpca_0[y==2, 1],              color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_kpca_1[y==0, 0], X_kpca_1[y==0, 1],               color='red', marker='+', alpha=0.5)ax[1].scatter(X_kpca_1[y==1, 0], X_kpca_1[y==1, 1],              color='green', marker='s', alpha=0.5)ax[1].scatter(X_kpca_1[y==2, 0], X_kpca_1[y==2, 1],              color='blue', marker='o', alpha=0.5)ax[0].set_xlabel('PC1')ax[0].set_ylabel('PC2')ax[1].set_ylim([-1, 1])ax[1].set_yticks([])ax[1].set_xlabel('PC1')plt.show()

参考资料

.相关阅读