前端算法系统练习: 栈和队列篇

这是前端算法系统练习系列的第二篇——栈和队列篇。关于为什么要练习算法和数据结构,请见上一篇前端算法系统练习: 链表篇完结。我一直秉承学习这件事情一定要系统的观念,因此每次更新都是一个完整的专题,虽然比较长,但是看下来结构会很清晰,收获的是一块完整的知识和方法论。希望对你能有帮助!
栈&递归
有效括号
给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。左括号必须以正确的顺序闭合。注意空字符串可被认为是有效字符串。
示例:
输入: "()"
输出: true
来源: LeetCode第20题
代码实现
/**
* @param {string} s
* @return {boolean}
*/
var isValid = function(s) {
let stack = [];
for(let i = 0; i < s.length; i++) {
let ch = s.charAt(i);
if(ch == '(' || ch == '[' || ch == '{')
stack.push(ch);
if(!stack.length) return false;
if(ch == ')' && stack.pop() !== '(') return false;
if(ch == ']' && stack.pop() !== '[' ) return false;
if(ch == '}' && stack.pop() !== '{') return false;
}
return stack.length === 0;
};
多维数组 flatten
将多维数组转化为一维数组。
示例:
[1, [2, [3, [4, 5]]], 6] -> [1, 2, 3, 4, 5, 6]
代码实现
/**
* @constructor
* @param {NestedInteger[]} nestedList
* @return {Integer[]}
*/
let flatten = (nestedList) => {
let result = [];
let fn = function (target, ary) {
for (let i = 0; i < ary.length; i++) {
let item = ary[i];
if (Array.isArray(ary[i])) {
fn(target, item);
} else {
target.push(item);
}
}
}
fn(result, nestedList)
return result;
同时可采用 reduce 的方式, 一行就可以解决,非常简洁。
let flatten = (nestedList) => nestedList.reduce((pre, cur) => pre.concat(Array.isArray(cur) ? flatten(cur): cur), [])
二叉树层序遍历
二叉树的层序遍历本是下一章的内容,但是其中队列的性质又体现得太明显,因此就以这样一类问题来让大家练习队列的相关操作。这里会不仅仅涉及到普通的层序遍历, 而且涉及到变形问题,让大家彻底掌握。
普通的层次遍历
给定一个二叉树,返回其按层次遍历的节点值。(即逐层地,从左到右访问所有节点)。
示例:
3
/ \
9 20
/ \
15 7
结果应输出:
[
[3],
[9,20],
[15,7]
]
来源: LeetCode第102题
实现
/**
* @param {TreeNode} root
* @return {number[][]}
*/
var levelOrder = function(root) {
if(!root) return [];
let queue = [];
let res = [];
let level = 0;
queue.push(root);
let temp;
while(queue.length) {
res.push([]);
let size = queue.length;
// 注意一下: size -- 在层次遍历中是一个非常重要的技巧
while(size --) {
// 出队
let front = queue.shift();
res[level].push(front.val);
// 入队
if(front.left) queue.push(front.left);
if(front.right) queue.push(front.right);
}
level++;
}
return res;
};
二叉树的锯齿形层次遍历
给定一个二叉树,返回其节点值的锯齿形层次遍历。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
例如:
给定二叉树 [3,9,20,null,null,15,7], 输出应如下:
3
/ \
9 20
/ \
15 7
返回锯齿形层次遍历如下:
[
[3],
[20,9],
[15,7]
]
来源: LeetCode第103题
思路
这一题思路稍微不同,但如果把握住层次遍历的思路,就会非常简单。
代码实现
var zigzagLevelOrder = function(root) {
if(!root) return [];
let queue = [];
let res = [];
let level = 0;
queue.push(root);
let temp;
while(queue.length) {
res.push([]);
let size = queue.length;
while(size --) {
// 出队
let front = queue.shift();
res[level].push(front.val);
if(front.left) queue.push(front.left);
if(front.right) queue.push(front.right);
}
// 仅仅增加下面一行代码即可
if(level % 2) res[level].reverse();
level++;
}
return res;
};
二叉树的右视图
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例:
输入: [1,2,3,null,5,null,4]
输出: [1, 3, 4]
解释:
1 <---
/ \
2 3 <---
\ \
5 4 <---
来源: LeetCode第199题
思路
右视图?如果你以 DFS 即深度优先搜索的思路来想,你会感觉异常的痛苦。没错,当初我就是这样被坑的:)
但如果用广度优先搜索的思想,即用层序遍历的方式,求解这道题目也变得轻而易举。
代码实现
/**
* @param {TreeNode} root
* @return {number[]}
*/
var rightSideView = function(root) {
if(!root) return [];
let queue = [];
let res = [];
queue.push(root);
while(queue.length) {
res.push(queue[0].val);
let size = queue.length;
while(size --) {
// 一个size的循环就是一层的遍历,在这一层只拿最右边的结点
let front = queue.shift();
if(front.right) queue.push(front.right);
if(front.left) queue.push(front.left);
}
}
return res;
};
无权图 BFS 遍历
完全平方数
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, ...)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
示例:
输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.
来源: LeetCode第279题
思路
这一题其实最容易想到的思路是动态规划,我们放到后面专门来拆解。实际上用队列进行图的建模,也是可以顺利地用广度优先遍历的方式解决的。
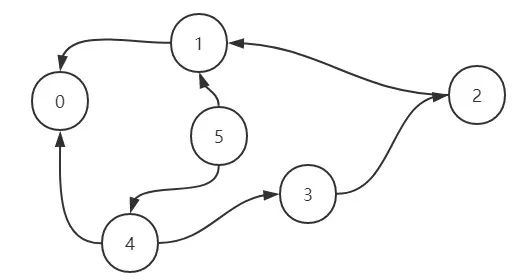
看到这个图,你可能会有点懵,我稍微解释一下你就明白了。
在这个无权图中,每一个点指向的都是它可能经过的上一个节点。举例来说,对 5 而言,可能是 4 加上了1的平方转换而来,也可能是1 加上了2的平方转换而来,因此跟1和2都有联系,依次类推。
那么我们现在要做了就是寻找到从 n 转换到 0 最短的连线数。
举个例子, n = 8 时,我们需要找到它的邻居节点4和7,此时到达 4 和到达 7 的步数都为 1, 然后分别从 4 和 7 出发,4 找到邻居节点3和0,达到 3 和 0 的步数都为 2,考虑到此时已经到达 0,遍历终止,返回到达 0 的步数 2 即可。
Talk is cheap, show me your code. 我们接下来来一步步实现这个寻找的过程。
实现
接下来我们来实现第一版的代码。
/**
* @param {number} n
* @return {number}
*/
var numSquares = function(n) {
let queue = [];
queue.push([n, 0]);
while(queue.length) {
let [num, step] = queue.shift();
for(let i = 1; ; i ++) {
let nextNum = num - i * i;
if(nextNum < 0) break;
// 还差最后一步就到了,直接返回 step + 1
if(nextNum == 0) return step + 1;
queue.push([nextNum, step + 1]);
}
}
// 最后是不需要返回另外的值的,因为 1 也是完全平方数,所有的数都能用 1 来组合
};
这个解法从功能上来讲是没有问题的,但是其中隐藏了巨大的性能问题,你可以去LeetCode去测试一下,基本是超时。
那为什么会出现这样的问题?
出就出在这样一行代码:
queue.push([nextNum, step + 1]);
只要是大于 0 的数,统统塞进队列。要知道 2 - 1 = 1, 5 - 4 = 1, 9 - 8 = 1 ......这样会重复非常多的 1, 依次类推,也会重复非常多的2,3等等等等。
这样大量的重复数字不仅仅消耗了更多的循环次数,同时也造成更加巨大的内存空间压力。
因此,我们需要对已经推入队列的数字进行标记,避免重复推入。改善代码如下:
var numSquares = function(n) {
let map = new Map();
let queue = [];
queue.push([n, 0]);
map.set(n, true);
while(queue.length) {
let [num, step] = queue.shift();
for(let i = 1; ; i++) {
let nextNum = num - i * i;
if(nextNum < 0) break;
if(nextNum == 0) return step + 1;
// nextNum 未被访问过
if(!map.get(nextNum)){
queue.push([nextNum, step + 1]);
// 标记已经访问过
map.set(nextNum, true);
}
}
}
};
单词接龙
给定两个单词(beginWord 和 endWord)和一个字典,找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则:
每次转换只能改变一个字母。 转换过程中的中间单词必须是字典中的单词。
说明:
如果不存在这样的转换序列,返回 0。 所有单词具有相同的长度。 所有单词只由小写字母组成。 字典中不存在重复的单词。 你可以假设 beginWord 和 endWord 是非空的,且二者不相同。
示例:
输入:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]
输出: 5
解释: 一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog",
返回它的长度 5。
来源: LeetCode第127题
思路
这一题是一个更加典型的用图建模的问题。如果每一个单词都是一个节点,那么只要和这个单词仅有一个字母不同,那么就是它的相邻节点。
这里我们可以通过 BFS 的方式来进行遍历。实现如下:
代码实现
/**
* @param {string} beginWord
* @param {string} endWord
* @param {string[]} wordList
* @return {number}
*/
var ladderLength = function(beginWord, endWord, wordList) {
// 两个单词在图中是否相邻
const isSimilar = (a, b) => {
let diff = 0
for(let i = 0; i < a.length; i++) {
if(a.charAt(i) !== b.charAt(i)) diff++;
if(diff > 1) return false;
}
return true;
}
let queue = [beginWord];
let index = wordList.indexOf(beginWord);
if(index !== -1) wordList.splice(index, 1);
let res = 2;
while(queue.length) {
let size = queue.length;
while(size --) {
let front = queue.shift();
for(let i = 0; i < wordList.length; i++) {
if(!isSimilar(front, wordList[i]))continue;
// 找到了
if(wordList[i] === endWord) {
return res;
}
else {
queue.push(wordList[i]);
}
// wordList[i]已经成功推入,现在不需要了,删除即可
// 这一步性能优化,相当关键,不然100%超时
wordList.splice(i, 1);
i --;
}
}
// 步数 +1
res += 1;
}
return 0;
};
实现优先队列
所谓优先队列,就是一种特殊的队列, 其底层使用堆的结构,使得每次添加或者删除,让队首元素始终是优先级最高的。关于优先级通过什么字段、按照什么样的比较方式来设定,可以由我们自己来决定。
要实现优先队列,首先来实现一个堆的结构。
关于堆的说明
可能你以前没有接触过堆这种数据结构,但是其实是很简单的一种结构,其本质就是一棵二叉树。但是这棵二叉树比较特殊,除了用数组来依次存储各个节点(节点对应的数组下标和层序遍历的序号一致)之外,它需要保证任何一个父节点的优先级大于子节点,这也是它最关键的性质,因为保证了根元素一定是优先级最高的。
举一个例子:
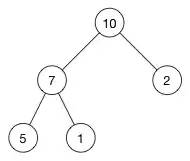
现在这个堆的数组就是: [10, 7, 2, 5, 1]
因此也会产生两个非常关键的操作——siftUp 和 siftDown。
对于siftUp操作,我们试想一下现在有一个正常的堆,满足任何父元素优先级大于子元素,这时候向这个堆的数组末尾又添加了一个元素,那现在可能就不符合堆的结构特点了。那么现在我将新增的节点和其父节点进行比较,如果父节点优先级小于它,则两者交换,不断向上比较直到根节点为止,这样就保证了堆的正确结构。而这样的操作就是siftUp。
siftDown是与其相反方向的操作,从上到下比较,原理相同,也是为了保证堆的正确结构。
实现一个最大堆
最大堆,即堆顶元素为优先级最高的元素。
// 以最大堆为例来实现一波
/**
* @param {number[]} nums
* @param {number} k
* @return {number[]}
*/
class MaxHeap {
constructor(arr = [], compare = null) {
this.data = arr;
this.size = arr.length;
this.compare = compare;
}
getSize() {
return this.size;
}
isEmpty() {
return this.size === 0;
}
// 增加元素
add(value) {
this.data.push(value);
this.size++;
// 增加的时候把添加的元素进行 siftUp
this._siftUp(this.getSize() - 1);
}
// 找到优先级最高的元素
findMax() {
if (this.getSize() === 0)
return;
return this.data[0];
}
// 让优先级最高的元素(即队首元素)出队
extractMax() {
// 1.保存队首元素
let ret = this.findMax();
// 2.让队首和队尾元素交换位置
this._swap(0, this.getSize() - 1);
// 3. 把队尾踢出去,size--
this.data.pop();
this.size--;
// 4. 新的队首 siftDown
this._siftDown(0);
return ret;
}
toString() {
console.log(this.data);
}
_swap(i, j) {
[this.data[i], this.data[j]] = [this.data[j], this.data[i]];
}
_parent(index) {
return Math.floor((index - 1) / 2);
}
_leftChild(index) {
return 2 * index + 1;
}
_rightChild(index) {
return 2 * index + 2;
}
_siftUp(k) {
// 上浮操作,只要子元素优先级比父节点大,父子交换位置,一直向上直到根节点
while (k > 0 && this.compare(this.data[k], this.data[this._parent(k)])) {
this._swap(k, this._parent(k));
k = this._parent(k);
}
}
_siftDown(k) {
// 存在左孩子的时候
while (this._leftChild(k) < this.size) {
let j = this._leftChild(k);
// 存在右孩子而且右孩子比左孩子大
if (this._rightChild(k) < this.size &&
this.compare(this.data[this._rightChild(k)], this.data[j])) {
j++;
}
if (this.compare(this.data[k], this.data[j]))
return;
// 父节点比子节点小,交换位置
this._swap(k, j);
// 继续下沉
k = j;
}
}
}
实现优先队列
有了最大堆作铺垫,实现优先队列就易如反掌,废话不多说,直接放上代码。
class PriorityQueue {
// max 为优先队列的容量
constructor(max, compare) {
this.max = max;
this.compare = compare;
this.maxHeap = new MaxHeap([], compare);
}
getSize() {
return this.maxHeap.getSize();
}
isEmpty() {
return this.maxHeap.isEmpty();
}
getFront() {
return this.maxHeap.findMax();
}
enqueue(e) {
// 比当前最高的优先级的还要高,直接不处理
if (this.getSize() === this.max) {
if (this.compare(e, this.getFront())) return;
this.dequeue();
}
return this.maxHeap.add(e);
}
dequeue() {
if (this.getSize() === 0) return null;
return this.maxHeap.extractMax();
}
}
怎么样,是不是非常简单?传说中的优先队列也不过如此。
且慢,可能会有人问: 你怎么保证这个优先队列是正确的呢?
我们不妨来做一下测试:
let pq = new PriorityQueue(3);
pq.enqueue(1);
pq.enqueue(333);
console.log(pq.dequeue());
console.log(pq.dequeue());
pq.enqueue(3);
pq.enqueue(6);
pq.enqueue(62);
console.log(pq.dequeue());
console.log(pq.dequeue());
console.log(pq.dequeue());
结果如下:
333
1
62
6
3
可见,这个优先队列的功能初步满足了我们的预期。后面,我们将通过实际的例子来运用这种数据结构来解决问题。
优先队列应用
前 K 个高频元素
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
示例:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
说明:
你可以假设给定的 k 总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。 你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
来源: LeetCode第347题
思路
首先要做的肯定是统计频率,那之后如何来选取频率前 K 个元素同时又保证时间复杂度小于 O(n log n)呢?
当然,这是一道典型的考察优先队列的题,利用容量为 K 的优先队列每次踢出不符合条件的值,那么最后剩下的即为所求。整个时间复杂度成为 O(n log K),明显是小于 O(n log n) 的。
既然是优先队列,就涉及到如何来定义优先级的问题。
倘若我们以高频率为高优先级,那么队首始终是高频率的元素,因此每次出队是踢出出现频率最高的元素,假设优先队列容量为 K,那照这么做,剩下的是频率最低的 K 个元素,显然不符合题意。
因此,我们需要的是每次出队时踢出频率最低的元素,这样最后剩下来的就是频率最高 K 个元素。
是不是我们为了踢出频率最低的元素,还要重新写一个小顶堆的实现呢?
完全不需要!就像我刚才所说的,合理地定义这个优先级的比较逻辑即可。接下来我们来具体实现一下。
代码实现
var topKFrequent = function(nums, k) {
let map = {};
let pq = new PriorityQueue(k, (a, b) => map[a] - map[b] < 0);
for(let i = 0; i < nums.length; i++) {
if(!map[nums[i]]) map[nums[i]] = 1;
else map[nums[i]] = map[[nums[i]]] + 1;
}
let arr = Array.from(new Set(nums));
for(let i = 0; i < arr.length; i++) {
pq.enqueue(arr[i]);
}
return pq.maxHeap.data;
};
合并 K 个排序链表
合并 k 个排序链表,返回合并后的排序链表。请分析和描述算法的复杂度。
示例:
输入:
[
1->4->5,
1->3->4,
2->6
]
输出: 1->1->2->3->4->4->5->6
这一题我们之前在链表篇实现过,殊不知,它也可以利用优先队列完美解决。
来源: LeetCode第23题
/**
* @param {ListNode[]} lists
* @return {ListNode}
*/
var mergeKLists = function(lists) {
let dummyHead = p = new ListNode();
// 定义优先级的函数,重要!
let pq = new PriorityQueue(lists.length, (a, b) => a.val <= b.val);
// 将头结点推入优先队列
for(let i = 0; i < lists.length; i++)
if(lists[i]) pq.enqueue(lists[i]);
// 取出值最小的节点,如果 next 不为空,继续推入队列
while(pq.getSize()) {
let min = pq.dequeue();
p.next = min;
p = p.next;
if(min.next) pq.enqueue(min.next);
}
return dummyHead.next;
};
怎么样,是不是被惊艳到!原来优先队列可以这样来使用!
双端队列及应用
什么是双端队列?
双端队列是一种特殊的队列,首尾都可以添加或者删除元素,是一种加强版的队列。
JS 中的数组就是一种典型的双端队列。push、pop 方法分别从尾部添加和删除元素,unshift、shift 方法分别从首部添加和删除元素。
滑动窗口最大值
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
要求: 时间复杂度应为线性。
来源: LeetCode第239题
思路
这是典型地使用双端队列求解的问题。
建立一个双端队列 window,每次 push 进来一个新的值,就将 window 中目前前面所有比它小的值都删除。利用双端队列的特性,可以从后往前遍历,遇到小的就删除之,否则停止。
这样可以保证队首始终是最大值,因此寻找最大值的时间复杂度可以降到 O(1)。由于 window 中会有越来越多的值被淘汰,因此整体的时间复杂度是线性的。
代码实现
代码非常的简洁,但是如果要写出 bug free 的代码还是有相当的难度的,希望你能自己独立实现一遍。
var maxSlidingWindow = function(nums, k) {
// 异常处理
if(nums.length === 0 || !k) return [];
let window = [], res = [];
for(let i = 0; i < nums.length; i++) {
// 先把滑动窗口之外的踢出
if(window[0] !== undefined && window[0] <= i - k) window.shift();
// 保证队首是最大的
while(nums[window[window.length - 1]] <= nums[i]) window.pop();
window.push(i);
if(i >= k - 1) res.push(nums[window[0]])
}
return res;
};
栈和队列的相互实现
栈实现队列
使用栈实现队列的下列操作:
push(x) -- 将一个元素放入队列的尾部。pop() -- 从队列首部移除元素。peek() -- 返回队列首部的元素。empty() -- 返回队列是否为空。
示例:
let queue = new MyQueue();
queue.push(1);
queue.push(2);
queue.peek(); // 返回 1
queue.pop(); // 返回 1
queue.empty(); // 返回 false
来源: LeetCode第232题
思路
既然栈是先进后出, 要想得到先进先出的效果,我们不妨用两个栈。
当进行push操作时,push 到 stack1,而进行pop和peek的操作时,我们通过stack2。
当然这其中有一个特殊情况,就是stack2是空,如何来进行pop和peek? 很简单,把stack1中的元素依次 pop 并推入stack2中,然后正常地操作 stack2即可,如下图所示:
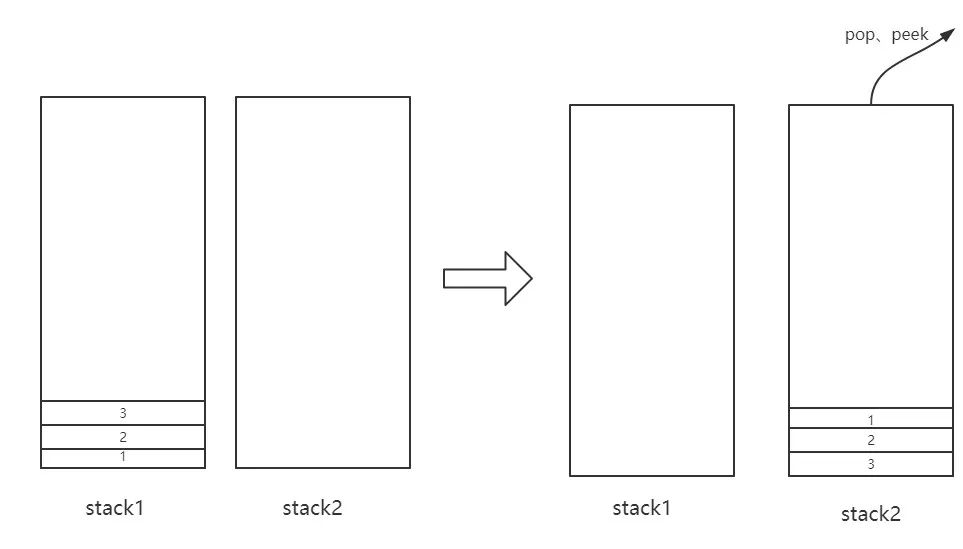
这就就能保证先入先出的效果了。
代码实现
var MyQueue = function() {
this.stack1 = [];
this.stack2 = [];
};
MyQueue.prototype.push = function(x) {
this.stack1.push(x);
};
// 将 stack1 的元素转移到 stack2
MyQueue.prototype.transform = function() {
while(this.stack1.length) {
this.stack2.push(this.stack1.pop());
}
}
MyQueue.prototype.pop = function() {
if(!this.stack2.length) this.transform();
return this.stack2.pop();
};
MyQueue.prototype.peek = function() {
if(!this.stack2.length) this.transform();
return this.stack2[this.stack2.length - 1];
};
MyQueue.prototype.empty = function() {
return !this.stack1.length && !this.stack2.length;
};
队列实现栈
和上一题的效果刚好相反,用队列先进先出的方式来实现先进后出的效果。
思路
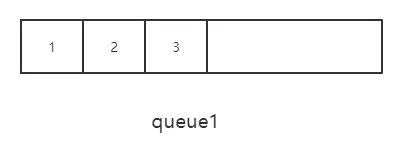
以上面的队列为例,push 操作好说,直接从在队列末尾推入。但 pop 和 peek 呢?
回到我们的目标,我们的目标是拿到队尾的值,也就是3。这就好办了,我们让前面的元素统统出队,只留队尾元素即可,剩下的元素让另外一个队列保存。
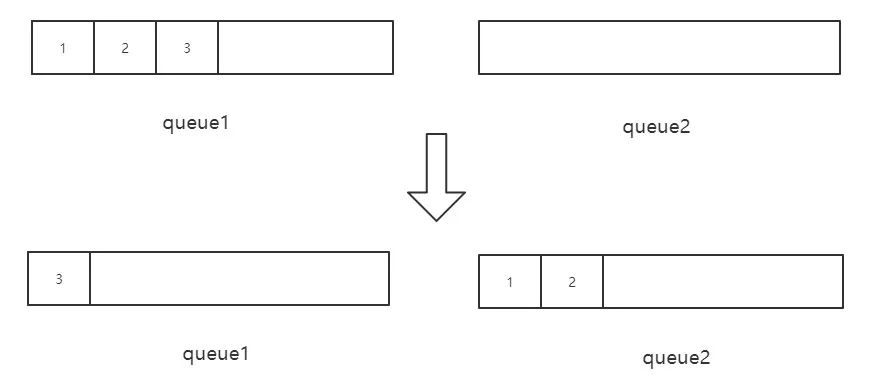
来源: LeetCode第225题
代码实现
实现过程中,值得注意的一点是,queue1 始终保存前面的元素,queue2 始终保存队尾元素(即栈顶元素 )。
但是当 push 的时候有一个陷阱,就是当queue2已经有元素的时候,不能将新值 push 到 queue1,因为此时的栈顶元素应该更新。此时对于新的值来说,应先 push 到 queue2, 然后将旧的栈顶从queue2出队,推入 queue1,这样就实现了更新栈顶的操作。
var MyStack = function() {
this.queue1 = [];
this.queue2 = [];
};
MyStack.prototype.push = function(x) {
if(!this.queue2.length) this.queue1.push(x);
else {
// queue2 已经有值
this.queue2.push(x);
// 旧的栈顶移到 queue1 中
this.queue1.push(this.queue2.shift());
}
};
MyStack.prototype.transform = function() {
while(this.queue1.length !== 1) {
this.queue2.push(this.queue1.shift())
}
// queue2 保存了前面的元素
// 让 queue1 和 queue2 交换
// 现在queue1 包含前面的元素,queue2 里面就只包含队尾的元素
let tmp = this.queue1;
this.queue1 = this.queue2;
this.queue2 = tmp;
}
MyStack.prototype.pop = function() {
if(!this.queue2.length) this.transform();
return this.queue2.shift();
};
MyStack.prototype.top = function() {
if(!this.queue2.length) this.transform();
return this.queue2[0];
};
MyStack.prototype.empty = function() {
return !this.queue1.length && !this.queue2.length;
};
