栈和队列-技术圈

本篇文章是视频课程《老汤 83 小时精讲：数据结构与算法【动画+手写代码】》中的《基础篇二：线性结构及其算法》栈和队列相关的文字总结

注意：文字讲解少了很多动态演示，也少了不少的代码演示，如果文章看得不是很明白的话，请看视频讲解

视频课程可以通过长按识别下面的二维码找到：

本篇文章的主要内容包括：

栈（Stack）

栈的应用一：方法的系统调用栈
栈的应用二：前进后退功能
栈的代码实现：分别使用数组和链表实现

队列（Queue）

使用数组实现队列
使用单向链表实现队列
优化单向链表实现的队列
优化数组实现的队列：循环队列

前面我们讲解了两种最基本的线性表结构：数组和链表，从这节课开始，我们再讲解两个使用比较广泛的线性表结构，那就是栈和队列。

栈（Stack）

我们知道不管是数组还是链表都允许从两端操作数据，比如都支持 addFirst、getFirst、addLast 以及 getLast 操作，如下图：

但是，我们今天要讲的栈就是操作受限的数据结构，对于一种线性表结构，如果我们只能对它的一端进行操作的话，那么这种数据结构就是栈了，如下图：

由于栈只能操作一端的数据，这就使得栈有一个最基本的特点：后进先出 (Last In First Out，简称 LIFO)。如下图：

可以看出：

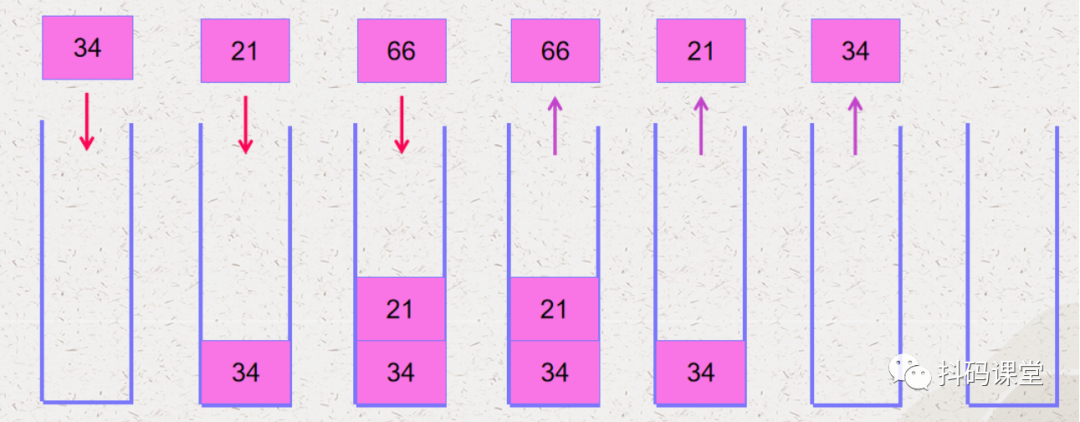
元素进栈的顺序是：34、21、66
元素出栈的顺序是：66、21、34

也就是说，后面进来的元素，优先出栈。这就是栈的特点：后进先出

对于栈，还有两个最基本的概念名词：

栈顶：可以操作数据的一端称为栈顶
栈底：不可以操作数据的一端称为栈底

你可能会问，这种操作受限的线性表数据结构到底有什么用呢？我们接下来举两个栈的使用场景的例子。

栈的应用一：方法的系统调用栈

在计算机的编程语言中，方法的调用是通过系统调用栈来实现的，我们看如下的代码：

public static void main(String[] args) {     a(10);}
public static int a(int x) {    int y = b(x, 1);    return y;}
public static int b(int x, int y) {    int sum = x + y;    c(sum);    return sum;}
public static void c(int x) {    System.out.println(x);}

以上 4 个方法的调用顺序是：main 方法 -> a 方法 -> b 方法 -> c 方法

在这里，被调用的方法执行结束的时候需要保证能正确回到调用方，比如：c 方法执行结束需要回到 b 方法，b 方法执行结束需要回到 a 方法，a 方法执行结束需要回到 main 方法，这个方法刚好和调用顺序相反，即 c 方法 -> b 方法 -> a 方法 -> main 方法

上面的方法调用实际上和栈的进栈出栈的操作是非常吻合的，符合后进先出的特点，所以我们可以使用栈来完成方法的调用

实际上，在方法调用前，JVM 会分配一个系统调用栈，方法的调用的顺序就是方法进栈的顺序，方法调用结束回到调用方的顺序就是出栈的顺序了。

栈的应用二：前进后退功能

对于编写代码的工具上的前进后退功能你肯定用过，比如 IDEA 上的前进后退功能：

我们在写代码的时候，会在 IDEA 中留下很多的操作痕迹，比如你在 IDEA 中打开了一个文件，然后依次做了一系列的操作：操作1 -> 操作2 -> 操作3 -> 操作4

这个时候，如果你想回到操作2，那么返回的顺序就是：操作4 -> 操作3 -> 操作2 。这个返回的顺序和之前操作的顺序是相反的，也符合后进先出的特点，所以我们可以使用栈来实现：

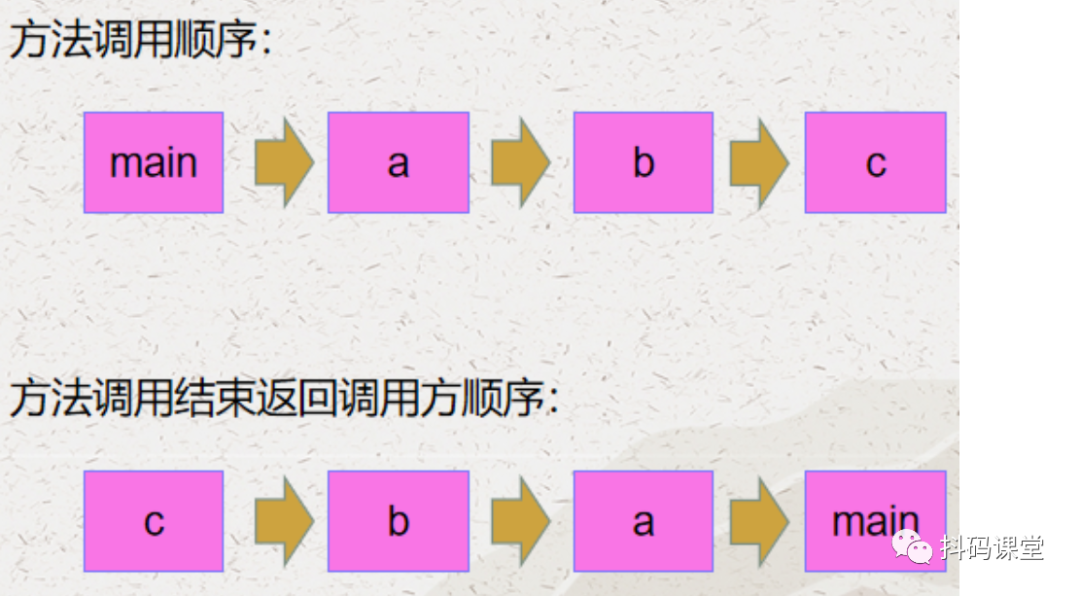
首先使用栈来记录每一个操作，用户每操作过一次就将操作压入栈中
等用户想返回的时候，只需要将操作出栈即可

到现在为止，我们实现了后退功能，还有一个前进功能呢？你会发现，前进功能要做的事情和后退功能一样，只是顺序刚好相反而已。我们可以使用第二个栈来实现前进功能。

用户的操作都压入到第一个栈中：

当用户需要后退的时候，将第一个栈中的栈顶操作出栈，然后将出栈的操作再次压入到第二个栈中
当用户需要前进的时候，将第二个栈中的栈顶操作出栈，然后将出栈的操作再次压入到第一个栈中

这样，我们就能完成后退前进功能。

栈的实现

栈最主要的两个操作是：

push 操作：向栈中压入元素
pop 操作：从栈中弹出栈顶元素

栈是一个操作受限的线性结构，也就是我们只能对一端进行操作，所以我们可以基于数组和链表分别来实现栈

在使用数组来实现栈的时候，我们只对数组的末端进行操作：

push 操作：向数组的末尾追加元素，这个操作的时间复杂度是 O(1)
pop 操作：将数组末尾的元素删除掉，注意，这里并不要真的删除末端元素，而是直接将 size-- 即可，这样可以实现常量级别的时间复杂度

在使用单向链表来实现栈的时候，我们只对链表的表头进行操作：

push 操作：向单向链表表头插入元素，这个操作是常量级别的时间复杂度
pop 操作：将单向链表的表头删除，这个操作也是常量级别的时间复杂度

可以看出，不管是使用数组还是单向链表实现栈，push 和 pop 的时间复杂度都是 O(1)

注意：代码实现请见视频讲解

队列 (Queue)

和栈一样，队列是操作受限的线性数据结构，但是和栈不一样的是，队列是一种先进先出的数据结构。

我们只能：

从一端将数据添加到队列中，这个过程我们称为入队 (enqueue)
从另一端将数据从队列中删除，这个过程我们称为出队 (dequeue)

一般而言，入队的一端我们称为队尾，出队的一端我们称为队首

和栈一样，队列可以使用数组、也可以使用链表来实现。

一、使用数组实现队列

使用数组来实现队列，我们需要先确定两个问题：

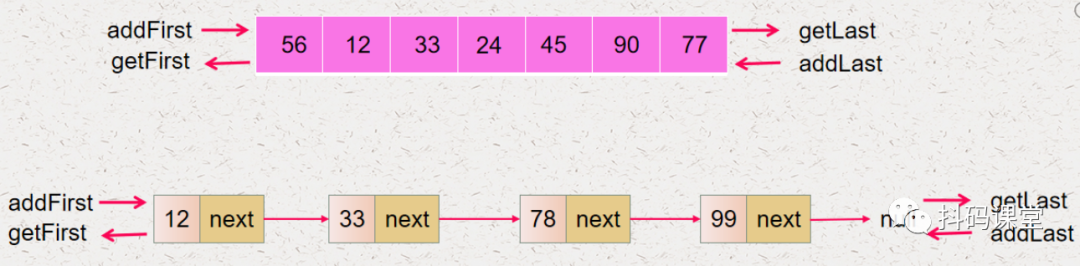
到底使用静态数组还是动态数组，这要看实现的队列是固定容量的还是动态容量的，我们这里先实现一个动态容量的队列，所以使用动态数组来实现
到底使用数组的哪一端作为队首，哪一端作为队尾，我们看下面的分析

如果选数组的尾作为队首的话，那么：

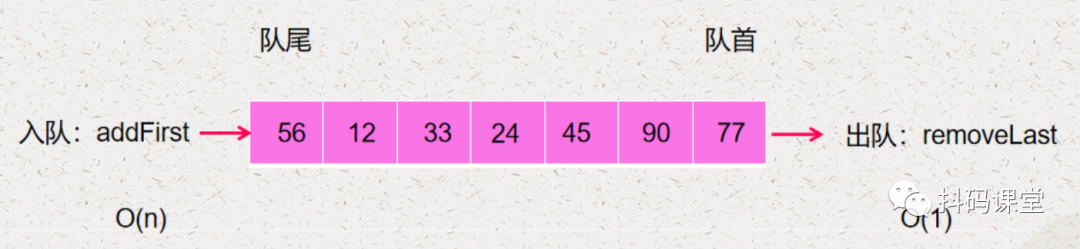
入队的操作就是 addFirst，它的时间复杂度是 O(n)
出队的操作就是 removeLast，它的时间复杂度是 O(1)

如果选数组的头作为队首的话，那么：

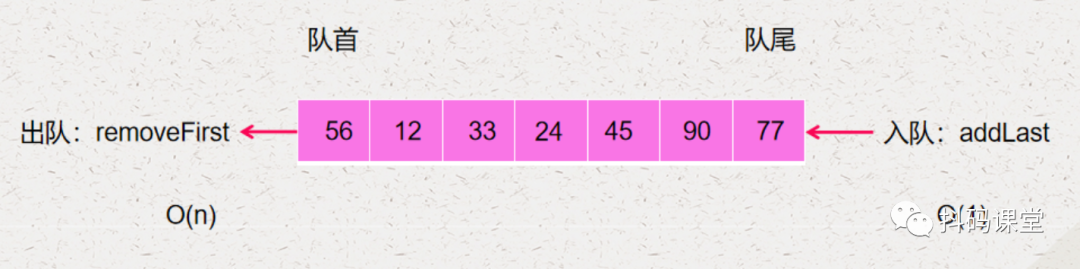
入队的操作就是 addLast，它的时间复杂度是 O(1)
出队的操作就是 removeFirst，它的时间复杂度是 O(n)

所以说。不管选哪个端作为队首，时间复杂度都是一样的，都会有一个操作是 O(n)，一个是 O(1)，所以选哪一端作为队首都一样

注意：代码实现请见视频讲解

二、使用单向链表实现队列

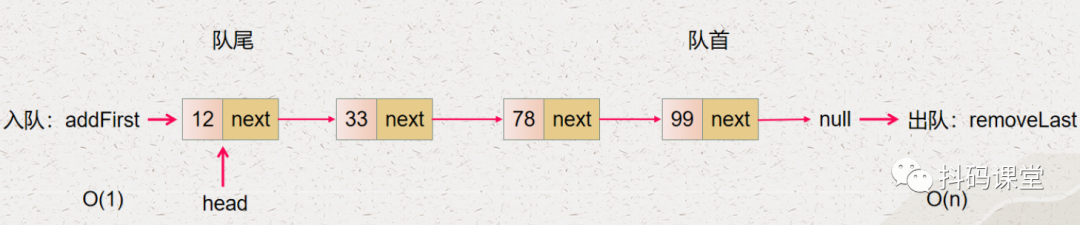
使用单向链表实现队列的话需要确定使用链表的哪一头作为队首，我们分别来讨论下

如果选单向链表的尾作为队首的话，那么：

入队的操作就是 addFirst，它的时间复杂度是 O(1)
出队的操作就是 removeLast，它的时间复杂度是 O(n)

如果选链表的头作为队首的话，那么：

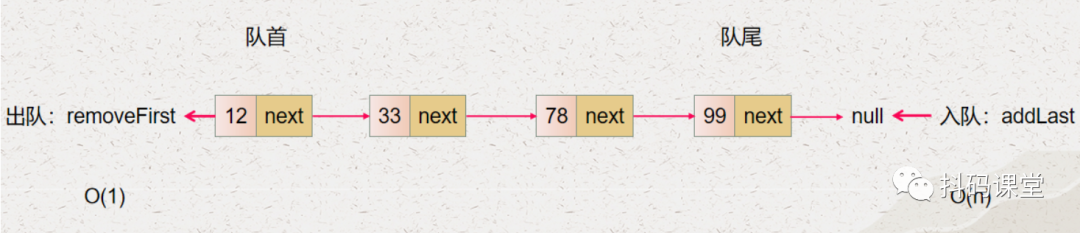
入队的操作就是 addLast，它的时间复杂度是 O(n)
出队的操作就是 removeFirst，它的时间复杂度是 O(1)

所以说。不管选哪个端作为队首，时间复杂度都是一样的，都会有一个操作是 O(n)，一个是 O(1)，所以选哪一端作为队首都一样

注意：代码实现请见视频讲解

三、优化单向链表实现的队列

我们使用单向链表实现了队列，不管是以链表的哪一端作为队首，队列中的出队和入队两个操作肯定会有一个操作的时间复杂度是 O(n)，我们能不能将这个时间复杂度降为 O(1) 呢？

我们要优化时间复杂度，先要找到导致时间复杂度高的原因，我们先看看下面的两张图：

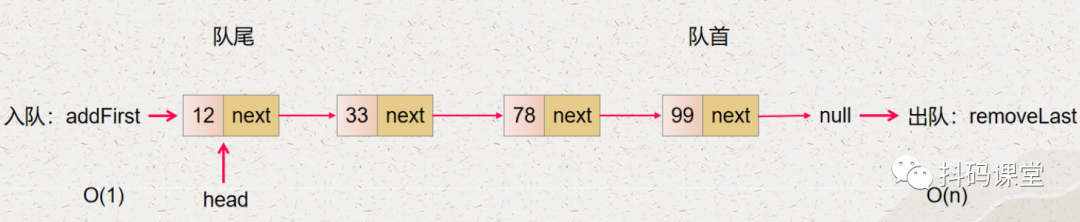
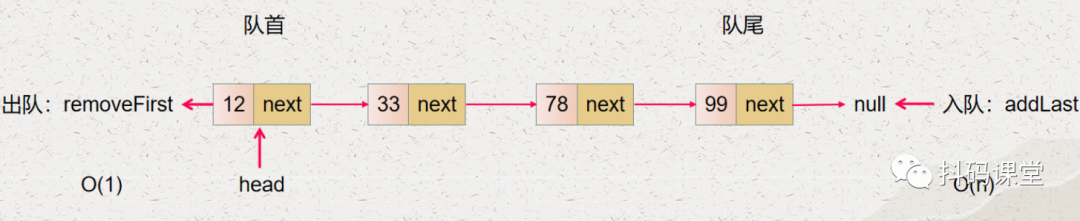
从图中就可以看出，导致时间复杂度为 O(n) 的原因就是我们对单向链表的最后一个节点的操作的时间复杂度都是 O(n)

之所以对最后一个节点的操作的时间复杂度是 O(n)，是因为每次操作最后一个节点，都需要从头节点往后遍历一遍单向链表

所以，我们要降低单向链表实现的队列出队入队的时间复杂度，那么就要降低对单向链表最后一个节点操作的时间复杂度。

我们现在回想下，为什么对单向链表的头不管是删除还是新增操作的时间复杂度是 O(1) 呢？答案就是我们通过一个变量 head 记住了链表头节点的位置，所以对头的操作的时间复杂度可以为常量级别

借助这个方法，我们也可以使用一个变量 tail 来记住单向链表的尾节点，看看能不能降低对尾节点的操作时间复杂度呢？

当我们使用一个变量 tail 来记住尾节点的位置的时候，对尾节点操作的时间复杂度确实发生了变化：

removeLast 操作的时间复杂度还是 O(n)，之所以时间复杂度没有变化，是因为要删除最后一个节点，就需要找到最后一个节点的前一个节点，然而对于单向链表，要找到最后一个节点的前一个节点需要从头节点开始遍历找到，所以时间复杂度还是 O(n)
addLast 操作的时间复杂度变成了 O(1)，这个是因为在最后一个节点后面新增一个节点，只需要知道最后一个节点的位置即可，然而我们已经使用 tail 变量记录了最后一个节点的位置了。

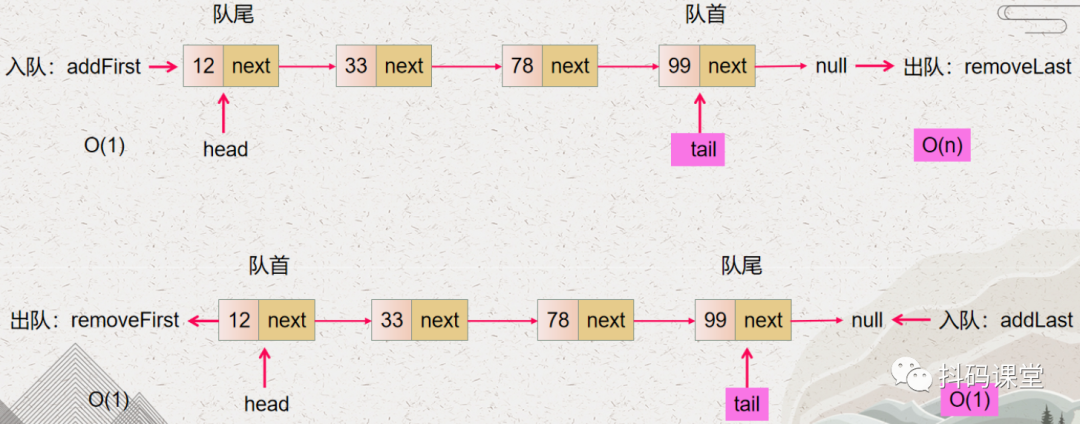
从上图，我们也可以得出一个结论：要使得单向链表实现的队列的出队和入队操作的时间复杂度都是 O(1) 的话，那么必须使用单向链表表头做队首。

以上，我们是使用单向链表 + 表头表尾两个指针来实现队列，而且实现的出队和入队的时间复杂度都是 O(1)

当然，你完全可以使用双向链表来实现队列，这样出队和入队的时间复杂度也是 O(1)

但是直接使用双向链表实现的队列，比使用单向链表 + 表头表尾两个指针实现的队列更加的耗费空间，因为双向链表的每个节点都多了一个前置指针

注意：代码实现请见视频讲解

四、循环队列

前面我们对使用单向链表实现的队列进行了优化，使得出队和入队的时间复杂度都是 O(1)

那么，我们能不能对数组实现的队列也进行优化呢？答案是可以的，那就是接下来要讲解的循环队列了

前面使用数组实现的队列，不管是以数组的哪一端作为队首，实现的队列的出队和入队两个操作总会有一个操作的时间复杂度是 O(n)，我们能不能将这个时间复杂度降为 O(1) 呢？

现在我们就来对前面的数组实现的队列进行优化。

我们要优化时间复杂度，先要找到导致时间复杂度高的原因，我们先看看下面的两张图：

从上图可以看出，用数组实现的队列之所以有时间复杂度为 O(n) 的操作，是因为我们对数组的第一个元素进行操作的时间复杂度都是 O(n)。

不管是删除第一个元素还是在第一个元素之前新增元素，都需要移动第一个元素后面所有的元素。

我们要是能在第一个元素出队的时候不移动后面的元素的话吗，那么就可以降低出队的时间复杂度。

要解决这个问题，我们可以引入两个变量，一个变量 head 来表示队列的头所在的数组的位置，另一个变量 tail 表示队尾下一个可以插入元素的位置，如下：

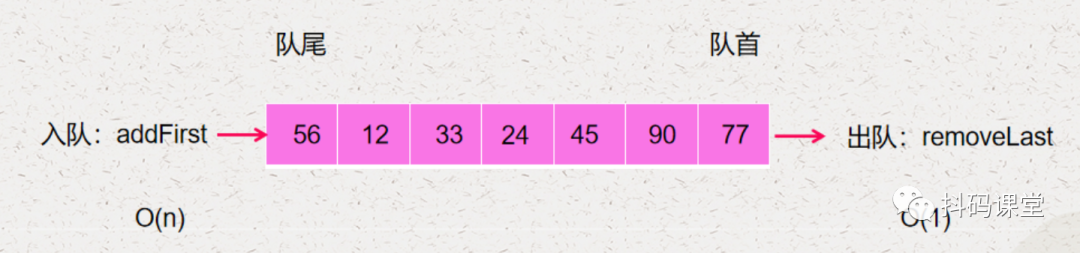
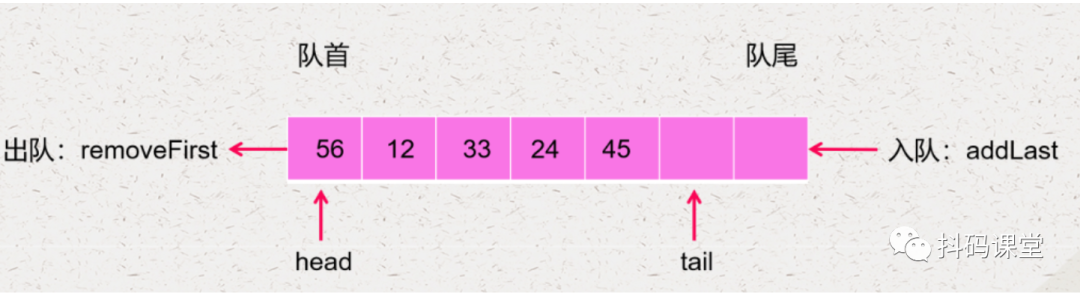
当第一个元素出队了，我们不需要移动剩下的元素，而是直接将 head 往后移动一位，如下：

当一个元素入队后，将 tail 往后移动一位即可，如下：

通过引用两个变量分别表示队首和队尾，从而消除了因为出队而引起的数据移动，所以这个时候的出队入队的时间复杂度就是 O(1) 了。

细心的同学可能会发现一个问题，就是当 tail 等于数组的长度，也就是 tail 到了数组的最末尾的话，那么这个时候如果有元素再想入队的话，该怎么办呢？

这个时候，如果数组前面还有空余的位置，那么元素就可以入队到数组的前面。这样我们实际上变成了一个循环数组了，我们通常叫这种队列为循环队列。

接下来，我们再解决两个问题：

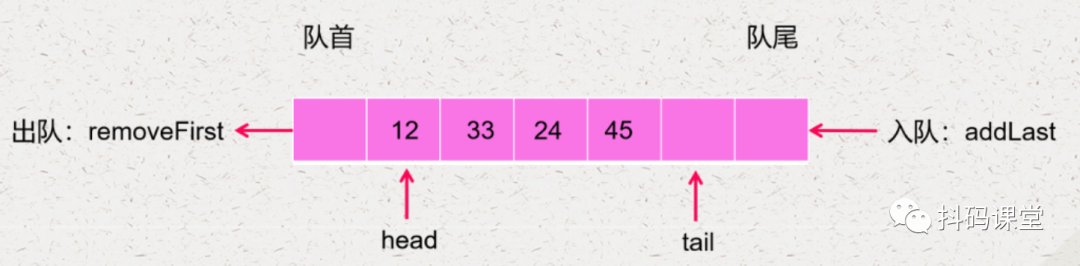
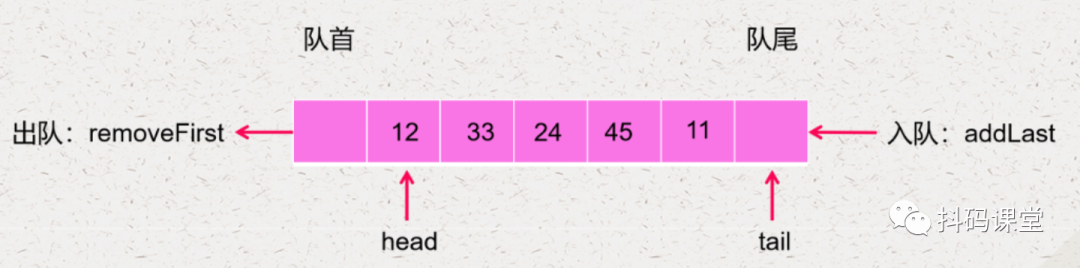
什么时候表示队列为空
什么时候表示队列已经满了

当队列初始化的时候，队列肯定是空的，这个时候 head 和 tail 两个变量都指向数组索引为 0 的位置上，如下图：

所以说，我们可以确定的是，当 head == tail 的时候，就表示队列为空了。

当队列中的元素排列成如下的状态：

请问，这个时候，我们还能将新元素入队吗？

假设我们现在将一个新元素入队的话，那么新元素入队后，head 就等于 tail 了，然而 head == tail 是队列为空的条件，实际上这个时候队列是满的

也就是说 head == tail 的时候既要表示队列为空，又要表示队列满了这两种状态，这个是不可能的事情。

为了解决这个问题，我们舍弃 head 前面的一个位置不存储元素，这个时候 tail 指向的就是这个空的元素，那么当队列达到这种状态的时候，表明队列已经满了。也就是说队列满的条件是 tail + 1 == head。

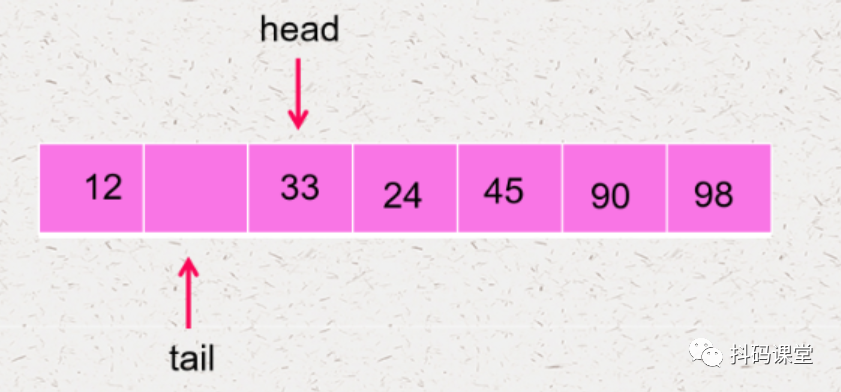
在实现循环队列之前，我们还有一个问题需要解决：head 和 tail 是怎么移动的？每次移动都 +1 吗？这样的话，head 和 tail 肯定会超出数据界限的，我们可以使用取模的手段，将 head 和 tail 控制在数组范围内，如下：

head = (head + 1) % data.length tail = (tail + 1) % data.length

注意：代码实现讲解请见视频讲解

循环队列的实现代码如下：

package com.douma.line.queue;
/** * @微信公众号 : 抖码课堂 * @官方微信号 : bigdatatang01 * @作者 : 老汤 */public class LoopQueue<E> implements Queue<E> {    private E[] data;    private int head;    private int tail;
    private int size;
    public LoopQueue() {        this(20);    }
    public LoopQueue(int capacity) {        data = (E[])new Object[capacity];        head = tail = 0;        size = 0;    }
    // 当前队列的容量    public int getCapacity() {        return data.length - 1;    }
    @Override    public int getSize() {        return size;    }
    @Override    public void enqueue(E e) {        if ((tail + 1) % data.length == head) {            // 队列满了            resize(getCapacity() * 2);        }        data[tail] = e;        size++;        tail = (tail + 1) % data.length;    }
    @Override    public E dequeue() { // O(1)        if (isEmpty()) {            throw new RuntimeException("dequeue error, No Element for dequeue");        }        E res = data[head];        data[head] = null;        size--;        head = (head + 1) % data.length;        if (size == getCapacity() / 4) {            resize(getCapacity() / 2);        }        return res;    }
    private void resize(int newCapacity) {        E[] newData = (E[])new Object[newCapacity + 1];        for (int i = 0; i < size; i++) {            newData[i] = data[(i + head) % data.length];        }        data = newData;        head = 0;        tail = size;    }
    @Override    public E getFront() {        return data[head];    }
    @Override    public boolean isEmpty() {        return head == tail;    }
    @Override    public String toString() {        StringBuilder sb = new StringBuilder();        sb.append(String.format("Queue：size = %d, capacity = %d\n", size, getCapacity()));        sb.append(" 队首 [");        for (int i = head; i != tail ; i = (i + 1) % data.length) {            sb.append(data[i]);            if ((i + 1) % data.length != tail) {                sb.append(",");            }        }        sb.append("]");        return sb.toString();    }}

码字不易，点赞、看一看两连即可。