三分钟基础:栈和队列
前期回顾:
今天直入重点,玩儿栈和队列,英文名 Stack and Queue,线性数据结构的典型代表,数组和链表的兄弟姐妹。
下面,让我们来看看,它们是有多简单。
栈
栈是一种后进先出(Last in First Out)的数据结构,简称 LIFO。
啥叫后进先出呢?这就和打飞机,呃,打手枪一样,弹夹中最先插进去的子弹最后才打出去,越晚摁进去的子弹越早打出来。
别小看它,栈是一种很重要的编程概念,它在软件应用中很常见。我们每天都用到的浏览器就用到了,浏览器的“后退”按钮。

比如臭宝上班的时候正在浏览器上看@编程文青李狗蛋的技术文,此时弹出一个保持男性持久的框框,“不小心”点到了,正看的入迷的时候你的老大路过,此时拿出单身 N 年的手速点击后退,你老大一看你在看帅蛋的文章,赞赏你是积极上进的员工,奖励手纸一卷。
看,“后退”是多么的有用~

栈的定义
那么,到底怎么定义栈呢?
很简单。
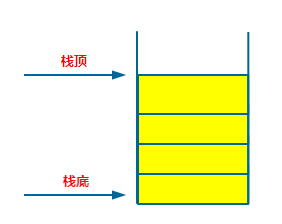
栈是限制仅在表的一端(表尾)进行操作(插入和删除)的线性表。
表尾又叫栈顶(Top),允许插入和删除,那么另一端就叫做栈底(Bottom),啥也不能干,只能干等着第一个进栈的过来躺着。
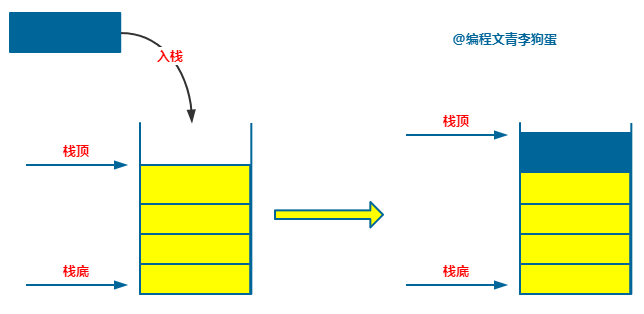
栈的插入操作,叫做入栈(push)。存入栈的元素之间没有任何具体的关系,只有到来的时间的先后顺序。
入栈操作涉及的单个数据的进入,所以时间复杂度为 O(1),同时入栈过程中只需要单个的临时存储空间,所以空间复杂度为 O(1)。
栈的删除操作,叫做出栈(pop)。删完了,也就是栈底就是栈顶的时候,就叫空栈。
同理,出栈操作涉及个别数据的出去且出栈过程只需要单个的临时存储空间,所以时间复杂度和空间复杂度都为 O(1)。
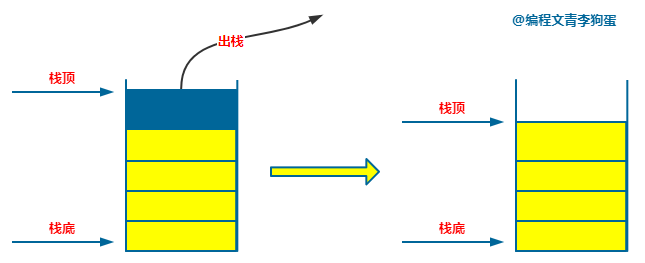
存入栈的元素之间没有任何具体关系,只有到来的时间的先后顺序.在这里没有元素的位置、元素的前后顺序等概念。
栈的存储结构
在上面说过,栈是线性表,那么它同样有顺序存储和链式存储。
顺序存储
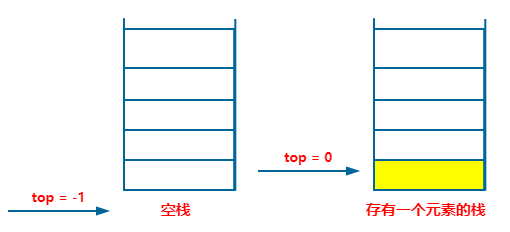
顺序存储的栈叫做顺序栈。
顺序栈使用数组实现,下标为 0 的一端作为栈底,使用 top 做为栈顶,它来指示当前栈顶元素的位置,默认 top = -1 时为空栈。
链式存储
链式存储的栈叫做链栈。
链栈用单链表实现,一般尾节点为栈底,使用头指针指向的节点作为栈顶,不需要头节点。top = NULL 为空栈。

啥同时因为顺序和链式本身的存储特点,顺序栈的元素个数是固定值,存在栈满的情况,而链式栈则不存在栈满的情况,除非内存被塞的满满的。
队列
队列是一种先进先出(First in First Out)的数据结构,简称 FIFO。
啥叫先进先出呢?这就和排队上厕所,谁先到谁先嘘嘘,到的晚的只能忍住。
同比栈,队列在软件应用中也很常见,就像现在我在一个字母一个字母的敲,最后输出在屏幕上你看到的一个个的字,这些就是最常见的队列的应用。
队列的定义
类比栈,怎么定义队列呢?
队列是限制仅在一端进行插入操作,在另一端进行删除操作的线性表。
允许插入的一端叫做队头,允许删除的一端叫做队尾。队列的插入叫做入队列,队列的删除叫做出队列。

队列的存储结构
同为线性表,队列也有链式存储和顺序存储。
链式存储
链式存储的队列叫做链队列。
其实这就是单链表,而且是带头节点的单链表,这样的话对于入队或者出队来说,它们的时间复杂度与单链表的插入和删除的时间复杂度都是一样的,都是 O(1)。
在此,头节点指向队头,用 head 指向头节点,tail 指向队尾。
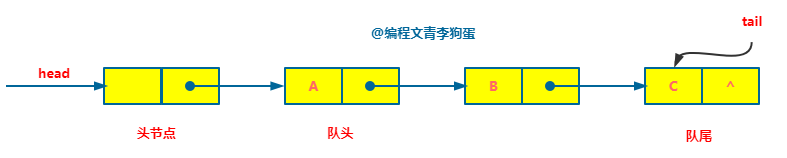
当 head 和 tail 都指向头节点时,为空队列。
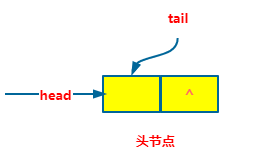
顺序存储
顺序存储的队列用数组实现。数组下标为 0 的一端为队头,用 head 指向,队尾用 tail 指向。
假设队列能存 5 个元素,当 head = tail,队列为空队列。
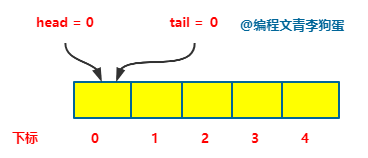
从上图的空栈中,A B C 依次入队,
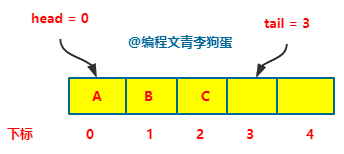
执行三次入队操作,此时head = 0,tail = 3。可以看出,当入队列的时候,数据直接按序存储到数组中,时间复杂度为 O(1)。
如果此时要执行两次出队操作。
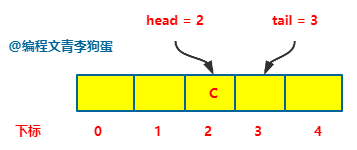
执行两次出队操作,相当于删除了 A B,此时 head = 2,tail = 3。从这可以看出,出栈的时间复杂度也是 O(1)。
是不是现在想说一句:就这?
还真不是就这。此时我再入两次队列。
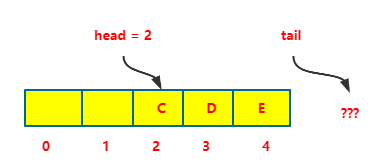
这个时候问题来了,我就大小为 5,数组最后一个元素已经被占了,此时再入栈的话,就数组越界了,但是我这个队列明明没满,我下标是 0 和 1 的位置还空着,这咋整?

不慌,两种办法。
第 1 种,满了就向前跑。
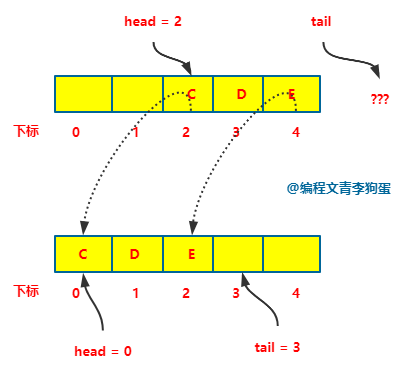
每次当 tail = n 的时候,所有的元素搬到 0 ~ (tail-head)的位置,这个时候入队的时间复杂度是 O(1) 或者 O(n),出队的时间复杂度也是 O(1)。
出队这个时间复杂度好理解,主要是入队为啥是 O(1) 或者 O(n)估计有点难理解。
可以这么来想,对于为 n 的数组,对于 tail 指向下标为 0 ~ (n-1) 的来说,入栈的时间复杂度都是 O(1),唯一不一样的是,当 tail = n 的时候数值需要向前跑,对于此时这步动作来说,时间复杂度为 O(n)。
跑动的这一步的 O(n) 可以均摊到 0 ~ (n-1) ,那么对于入队来说,平均时间复杂度就是 O(1)。
第 2 种,满了从头再来。
怎么从头再来呢?
当队列满了,那就是 tail = n,前面如果有空,那 tail = 0 不就又能再来啦。
怎么让 tail = n 了以后再编程 tail = 0,那不就是首尾相连,循环队列就这么闪亮登场了。

循环队列
循环队列,就是队列的队头和队尾相接的顺序存储结构。
如果是循环队列的话,那当队列满了 tail 不需要等于 n ,直接指向了下标为 0 的位置。
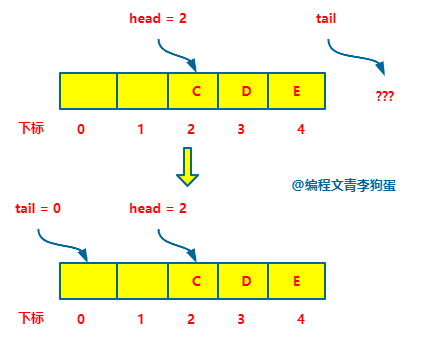
如果此时要执行入队操作,那就会变成:
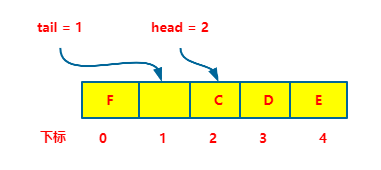
如果想更直观一些,我可以把它掰弯了给大家看。
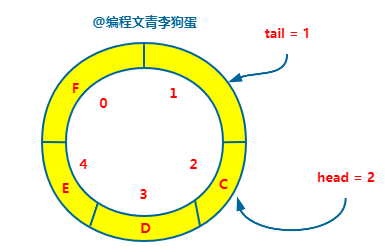
你仔细看上面那张图,你会发现一个问题,如果再入队一个元素的话,队列满了,此时 tail = head。
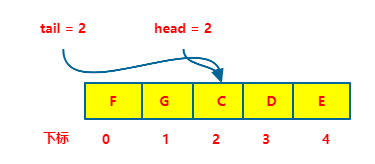
那问题来了,队列空的时候 tail = head,现在队列满了,也是 tail = head,我傻了呀,我怎么知道现在的队列是啥状态呢?
那只能有一者做出牺牲了,空队列啥也没有,显然和个废物没啥两样,所以只能满队列做牺牲,牺牲一个位置啥也不放,也就是 tail 和 head 相差为 1 的时候就队列满了。也就是下面这种。

因为 tail 可能比 head 大(正常占用完)也可能比 head 小(做了循环),所以判断队列满的条件就成了 (tail + 1) % n = head。
栈和队列到这就讲完啦,哎呀妈呀画了这么多图可累死我了,虽然丑丑的...

再往下面搞就是栈和队列的实战了,敬请期待我的不定时上线。
看到这的都是真爱,点赞在看留言么么哒给我刷起来~
我是蛋蛋,我们下次见!

