算法工程师面试必考项——栈与队列-技术圈

AI编辑：田旭

AI作者：田旭

1 知识点

1.1 栈

堆栈（英语：stack）又称为栈或堆叠，是计算机科学中的一种抽象数据类型，只允许在有序的线性数据集合的一端（称为堆栈顶端，英语：top）进行加入数据（英语：push）和移除数据（英语：pop）的运算。因而按照后进先出（LIFO, Last In First Out）的原理运作。

栈常用一维数组或链表来实现。

栈使用两种基本操作：推入（压栈，push）和弹出（弹栈，pop）：

推入：将数据放入堆栈顶端，堆栈顶端移到新放入的数据。
弹出：将堆栈顶端数据移除，堆栈顶端移到移除后的下一笔数据。

栈的基本特点：

先入后出，后入先出。
除头尾节点之外，每个元素有一个前驱，一个后继。

栈中的每个元素称为一个frame。而最上层元素称为top frame。栈只支持三个操作， pop, top, push。

pop取出栈中最上层元素(8)，栈的最上层元素变为早先进入的元素(9)。

top查看栈的最上层元素(8)。

push将一个新的元素(5)放在栈的最上层。

栈不支持其他操作。如果想取出元素12, 必须进行3次pop操作。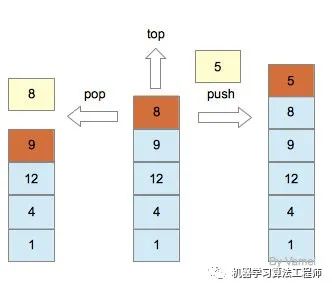

1.2 队列

队列（queue）是一种采用先进先出(FIFO)策略的抽象数据结构，即最先进队列的数据元素，同样要最先出队列。队列跟我们排队买票一样，先来排队的肯定先买票，后来排队的的后买到票。队列如下图所示：

队列有两个重要的概念，一个叫队头，一个叫队尾，队头指向的是第一个元素，而队尾指向的是最后一个元素。队列跟栈一样也是访问受限制的，所以队列也只有两个主要的操作：入队(enqueue)操作 和 出队(dequeue)操作 。入队操作就是将一个元素添加到队尾，出队操作就是从队头取出一个元素。

队列的底层实现可以用数组和链表，基于数组实现的队列叫作顺序队列，基于链表实现的队列叫作链式队列

队列的操作方式和栈类似，唯一的区别在于队列只允许新数据在后端进行添加。

2 常见面试题

2.1 栈

155. 最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。
push(x) —— 将元素 x 推入栈中。pop() —— 删除栈顶的元素。top() —— 获取栈顶元素。getMin() —— 检索栈中的最小元素。

class MinStack:
    def __init__(self):        """        initialize your data structure here.        """        self.stack = []        self.minx = []   # 利用辅助栈来存储最小值
    def push(self, x: int) -> None:        self.stack.append(x)        if not self.minx or x <= self.minx[-1]:  # 如果minx没有元素，或者当前x小于等于辅助栈顶元素，则将当前x存入辅助栈顶            self.minx.append(x)
    def pop(self) -> None:        if self.stack.pop() == self.minx[-1]: # 先进行stack.pop()，如果去除元素与辅助栈顶元素相同，则辅助栈也去除元素            self.minx.pop()
    def top(self) -> int:        return self.stack[-1]  # 返回数据栈顶元素
    def getMin(self) -> int:        return self.minx[-1]   # 返回辅助栈顶元素

# Your MinStack object will be instantiated and called as such:# obj = MinStack()# obj.push(x)# obj.pop()# param_3 = obj.top()# param_4 = obj.getMin()

150. 逆波兰表达式求值

根据逆波兰表示法，求表达式的值。
有效的运算符包括 +, -, *, / 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

思路：利用栈的思想，如果是数字，则压入栈；若为符号，即执行“pop取栈顶 -> pop取新栈顶 -> 计算”操作。

class Solution:    def evalRPN(self, tokens: List[str]) -> int:        symbol = ["+", "-", "*", "/"]        resList = []        if len(tokens) == 0:            return 0        else:            for c in tokens:                if c not in symbol:                    resList.append(int(c))                else:                    b = resList.pop()                    a = resList.pop()                    if c == "+":                        resList.append(a+b)                    elif c == "-":                        resList.append(a-b)                    elif c == "*":                        resList.append(a*b)                    elif c == "/":                        resList.append(int(a/b))        return resList[0]

394. 字符串解码

给定一个经过编码的字符串，返回它解码后的字符串。
编码规则为: k[encoded_string]，表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。

思路：通过辅助栈进行操作

class Solution:    def decodeString(self, s: str) -> str:        stack = []        res = ""        multi = 0        for c in s:            if "0" <= c <= "9":                multi = multi*10 + int(c)    # 考虑数字是2位以上的情况            elif c == "[":                stack.append([multi, res])   # 当前 multi 和 res 入栈，并分别置空置 00                multi = 0   # 重置                res = ""            elif c == "]":                cur_multi, last_res = stack.pop()  # 取出[]中的重复倍数和字符串                res = last_res + cur_multi * res   # 拼接字符串            else:                res += c   # 遇到其他，则当字母串处理        return res

利用栈进行 DFS 递归搜索模板

class Solution:    def decodeString(self, s: str) -> str:        def dfs(i):            res = ""            multi = 0            while i < len(s):                if '0' <= s[i] <= '9':                    multi = multi * 10 + int(s[i])                # 遇到'['开始将后续的string递归                elif s[i] == '[':                    i, temp = dfs(i + 1)                    # 注意，返回i的含义是更新上层递归指针位置，因为内层递归已经吃掉一串str，若不跟新i，外层仍然从i+1开始，则会重复处理内层处理过的一串str。                    res += multi * temp                    multi = 0                # 遇到']'到达递归边界，结束递归，返回新i和处理好的内层res                elif s[i] == ']':                    return i, res                else:                    res += s[i]                i += 1            return res        return dfs(0)

94. 二叉树的中序遍历

给定一个二叉树，返回它的中序遍历。

思路：通过stack 保存已经访问的元素，用于原路返回

class Solution:    def inorderTraversal(self, root: TreeNode) -> List[int]:        res = []        stack = []        while stack or root:            while root:                stack.append(root)                root = root.left            root = stack.pop()      # 此时左子树遍历完成            res.append(root.val)    # 将父节点加入列表            root = root.right       # 遍历右子树        return res

200. 岛屿数量

给定一个由 '1'（陆地）和 '0'（水）组成的的二维网格，计算岛屿的数量。一个岛被水包围，并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。

思路：通过深度搜索遍历可能性（注意标记已访问元素）

class Solution:    def numIslands(self, grid: List[List[str]]) -> int:        if not grid:            return 0        m, n = len(grid), len(grid[0])        res = 0        def backtrack(grid, i, j):            if i < 0 or i >=m or j < 0 or j >= n or grid[i][j] != '1':   # 判断边界                return            grid[i][j] = '0'    # 遍历过的地方都标记为0，避免重复寻找            backtrack(grid, i, j+1)            backtrack(grid, i+1, j)            backtrack(grid, i, j-1)            backtrack(grid, i-1, j)        for i in range(m):            for j in range(n):                if grid[i][j] == '1':                    backtrack(grid, i, j)                    res += 1        return res

133. 克隆图

给你无向连通图中一个节点的引用，请你返回该图的 深拷贝（克隆）。
图中的每个节点都包含它的值 val（int）和其邻居的列表（list[Node]）。

思路：遍历整个图，遍历时候要记录已经访问点，我们用一个字典记录。

# DFS 深度优先遍历class Solution:    def cloneGraph(self, node: 'Node') -> 'Node':        lookup = {}                def dfs(node):            if not node:                return            if node in lookup:                return lookup[node]            clone = Node(node.val, [])            lookup[node] = clone            for i in node.neighbors:                clone.neighbors.append(dfs(i))                        return clone                  return dfs(node)

# BFS 广度优先遍历class Solution:    def cloneGraph(self, node: 'Node') -> 'Node':        from collections import deque        lookup = {}                if not node:            return        clone = Node(node.val, [])        lookup[node] = clone        queue = deque()        queue.appendleft(node)        while queue:            temp = queue.pop()            for n in temp.neighbors:                if n not in lookup:                    lookup[n] = Node(n.val, [])                    queue.appendleft(n)                lookup[temp].neighbors.append(lookup[n])        return clone

84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积

# 优化中心扩展法class Solution:    def largestRectangleArea(self, heights: List[int]) -> int:        n = len(heights)        l, r, ans = [-1] * n, [n] * n, 0        for i in range(1, n):            j = i - 1            while j >= 0 and heights[j] >= heights[i]:                j = l[j]            l[i] = j        for i in range(n - 2, -1, -1):            j = i + 1            while j < n and heights[j] >= heights[i]:                j = r[j]            r[i] = j        for i in range(n):            ans = max(ans, heights[i] * (r[i] - l[i] - 1))        return ans

# 单调栈class Solution:    def largestRectangleArea(self, heights: List[int]) -> int:        """        头部加0便于处理当栈里只有一个有效元素要弹出的时候计算面积。        如果头部不加0，最后一个有效元素被弹出的时候，栈已经为空了，则还需要特殊处理。        尾部加0，如果0最后一个入栈，所有的数都会弹出        """        stack = []        heights = [0] + heights + [0]        res = 0        for i in range(len(heights)):            while stack and heights[stack[-1]] > heights[i]:                tmp = stack.pop()                res = max(res, (i - stack[-1] - 1) * heights[tmp])            stack.append(i)        return res

2.2 队列

232. 用栈实现队列

使用栈实现队列的下列操作：
push(x) -- 将一个元素放入队列的尾部。pop() -- 从队列首部移除元素。peek() -- 返回队列首部的元素。empty() -- 返回队列是否为空。

思路：定义两个栈，一个负责入栈，一个负责出栈，元素先进入入栈，再压入出栈

class MyQueue:
    def __init__(self):        """        Initialize your data structure here.        """        self.instack = []        self.outstack = []
    def push(self, x: int) -> None:        """        Push element x to the back of queue.        """        self.instack.append(x)
    def pop(self) -> int:        """        Removes the element from in front of queue and returns that element.        """        if not self.outstack:            while self.instack:                self.outstack.append(self.instack.pop())        return self.outstack.pop()
    def peek(self) -> int:        """        Get the front element.        """        if not self.outstack:            while self.instack:                self.outstack.append(self.instack.pop())        return self.outstack[-1]
    def empty(self) -> bool:        """        Returns whether the queue is empty.        """        return not self.instack and not self.outstack

542. 01 矩阵

给定一个由 0 和 1 组成的矩阵，找出每个元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。

思路：BFS，从0进队列，弹出之后计算上下左右的结果，将上下左右重新进队列进行二层操作

class Solution:    def updateMatrix(self, matrix: List[List[int]]) -> List[List[int]]:        m, n = len(matrix), len(matrix[0])        q = collections.deque([])        visited = set()        # 初始化队列，将所有起始点加入        for i in range(m):            for j in range(n):                if matrix[i][j] == 0:                    q.append((i, j))                    visited.add((i, j))        # 将所有相邻节点加入队列        while q:            i, j = q.popleft()            for x, y in [(i+1, j), (i-1, j), (i, j+1), (i, j-1)]:                if 0 <= x < m and 0 <= y < n and (x, y) not in visited:                    matrix[x][y] = matrix[i][j] + 1                    visited.add((x, y))                    q.append((x, y))        return matrix

参考资料

堆栈-维基百科
https://juejin.im/post/6844903928476368909
LeetCode题解
https://greyireland.gitbook.io/algorithm-pattern/shu-ju-jie-gou-pian/stack_queue

推荐阅读

机器学习算法工程师

一个用心的公众号