最小二乘法的本质是什么？

重磅干货，第一时间送达

本文转自：深度学习与计算机视觉

最小二乘法的一种常见的描述是残差满足正态分布的最大似然估计
模型具有如下形式:


是基函数
残差满足正态分布
于是有:
对于N个独立的样本


与独立
, 得到最大似然估:



得到最小欧式距离, 即是最小二乘法

假设我们需要预测每个省的在淘宝买东西花的钱 t 和该省平均房价 y 的关系，我们用数学符号表达下：  y = N(t) + e

这里的 N(t) 就是我们要找的数学模型，但是实际上我们永远也没有办法找的真的 N， 所以那就次点，找个近似的模型 M(t) 吧。为了判断这个 M 找的准不准，我们用实际的数据考察一下，也就是实际的房价和预测的房价的差，或者叫残差。如果残差的平方和很小，那么我们可以认为这个模型和之前的数据拟合的很好，这个就是我们要找的的模型啦。

回头看下，这个找模型的过程实际上是在找理想和预测差值的最小平方和。假设我们的模型很简单：.

我们用 表示第 i 个数据的残差， 。注意这里的 描述的是模型内部的系数，即

假设我们现在有 个数据，这 个残差的平方和用 来表示:

(忽略这里的1/2，为了后面微分的方便)。

以上就是最小2乘问题的介绍和定义。解决最小二乘问题实际上是求解方程 .

实际上像梯度法、高斯法、牛顿法、L-M法、狗腿法(Powell)、都是在解决非线性的最小二乘问题。

• 勾股定理和欧氏几何的平行公理等价。
• 平行公理定义欧氏空间。
• 欧氏空间是平坦的、线性的、各向同性的。（用爱因斯坦的话来说就是空间曲率为0）

实际上，高斯对于最小二乘法的认识，很有钦定的意味：假定最小二乘法最优，那么如何如何。至于为什么它最优，抱歉，高斯本人也不知道。

第一个真正证明最小二乘法最优的是Maxwell。他的证明主要基于空间对称性，而这正是欧氏空间的特点。

问题：什么时候最小二乘不好使？

回答：假如把你扔到1-范数空间，就不要用最小二乘了。那里的误差不满足正态分布，而是满足拉普拉斯分布。

Laplace：某个高票答案diss我不如Gauss，其实我只是跑到了另一个空间而已。

问题：不知道什么空间怎么办？

回答：还是用最小二乘吧。线性计算比较简单，而且采样足够多了，都是正态分布。（中心极限定理）

问题：最小二乘法的本质是什么？

回答：我也不清楚提问者想要什么样的本质。不过欧几里得可以用5条公理构建一个庞大的数学体系。公理应该算本质了吧。

就是说，有一堆数据，看着有点杂乱，但却体现出一定的规律，虽然不能构建一个函数，完全匹配数据的每个值，但是能够构建一个函数，大差不差的勾勒出大概的走向，然后预测未来数据的可能。

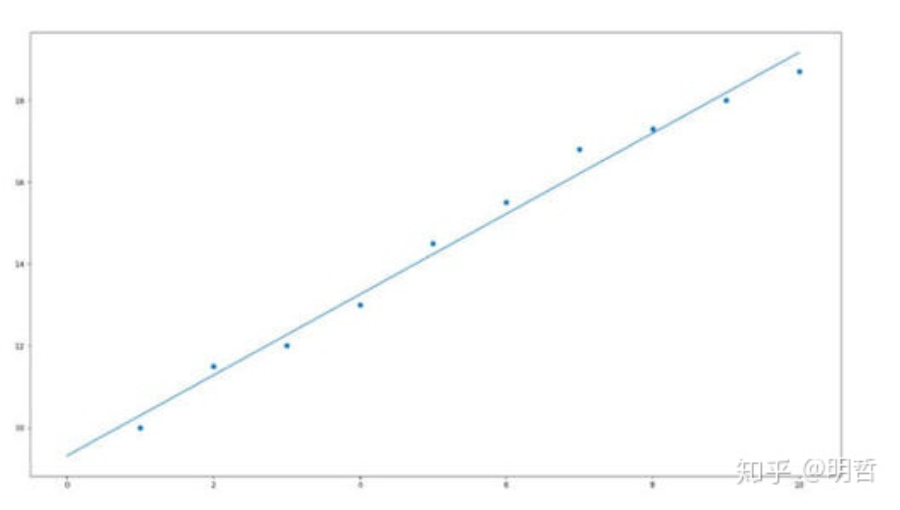
于是，要让所有这种距离的和的平方最小。

函数表达式为——

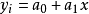
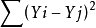
这就变成了多元函数最小化问题，求偏导，令偏导等于零，求出来再带入回去……

看上去这是个相当简单的任务，因为我们只要有两对精确的{x, y}的取值就可以通过求解线性方程组来得到w和b的取值了。

当然，这个思路是不正确的，否则我们也就不需要最小二乘法。那么这个思路错在哪里呢？显然，如果说这个思路是错的，那也就说明我们测量出来的{xi, yi}并不完全符合y=wx+b这个线性关系。产生这个问题的原因是，在现实任务当中，尽管x与y之间确实存在可以用这个线性式表示的相关关系，但我们可能因为测量方式、测量工具、眼斜、手抖或者等等其他因素而产生一定的误差。也就是说我们实际测量出的(xi, yi)所符合的模型其实是这样的：

其中epsilon代表我们测量的误差。

What???这个误差项我们又没法测量出来，那我们还怎么求w和b？没错，在无法彻底消除误差的情况下，我们永远都不能得到完全精确的w和b的取值。但是幸运的是，我们可以根据概率论去推测一个比较有可能的w和b的取值。

接下来就要说最小二乘法了。我们在使用最小二乘法的时候，实际上也就是在观测到一系列{xi, yi}的情况下去推测{w, b}的最靠谱的取值。

那怎么去推出这个最靠谱的取值呢？我们当然得先把其他不确定的量确定下来，这里说的就是这个误差epsilon。我们虽然不能确定epsilon的取值，但是我们可以假设epsilon满足一个分布。因为epsilon受到相当多因素的影响，根据中心极限定理，可以猜测epsilon服从高斯分布。也就是

在这个前提下，我们再去推测w和b。这里我们使用最大似然估计。

最大似然估计是什么意思呢？简单来说，就是w和b的哪个取值能让我们现在观测到的{x, y}显得最可能出现，那我们就认为w和b是多少。举个简单的情况，假如我们观测到了x=0,y=0，这时候我们回头看w和b。在w=0与b=0的情况下观测到x=0,y=0的概率是不低的，而在w=1000,b=10000的情况下，我们就不太可能观测到x=0,y=0了。所以我们在观测到x=0,y=0的情况下，我们认为w=0,b=0的可能性比w=1000,b=10000的可能性要大。

好了，我们回到刚才的问题。我们记我们对w和b的估计值为 。那在参数符合推测的情况下，我们观测到一对值(xi,yi)的概率为

可知在w,x,b确定的情况下 ，即

也就是

我们的目标也就要使得这个概率最大，即

可以看到，我们最终得到的最小化目标就是最小二乘法的最小化目标。也就是说在测量误差epsilon服从正态分布的前提下，我们只要求出一对 使得预测值与实际值的平方差之和最小，我们就可以保证这些观测值{x, y}的出现概率是最高的。

总结一下：从概率的角度理解，最小二乘法的本质其实就是在观测到一组实验值{x,y}的，并猜测测量误差服从正态分布的前提下，利用极大似然估计，去推测出w和b这两个参数的最靠谱的取值的过程。

知道E(Y)是不够的，还需要求出具体的条件概率P(Y|X)。最小二乘法实质上假定P(Y|X)服从均值为E(Y)，方差为1的正态分布，作为先验前提。然后根据经验集合的分布(即能拿来拟合回归的数据的分布)，认为其是数据真实分布的抽样，找出最可能的正态分布形式来，这里只要估计均值E(Y)就行了，因为方差已经假定是1。最后这个过程有点像装修的时候往水管里塞电线，先验是 水管的形状，要用 电线 塞进去，和水管的大致形状（因为水管内部还有一部分空间，电线还有一点点自由度）最像。

不过我这样讲，估计懂的人早懂了，不懂的也很难，具体思想可以参看 《DEEP LEARNING》 by GOODFELLOW 第五章。线性回归最小二乘法分别用 最大似然 相对熵 贝叶斯统计的角度实现，都是假定P(Y|X)符合正态分布，根据各家不同思想得到相同结果。

1. Estimation的基本原则就是误差向量e最小

2. Least Square Estimation的本质是让误差向量e的L2范数最小，等价于几何上的欧式距离最小（也就是做投影）

3. 为什么最小的是误差向量e的“二乘”而不是绝对值等等，就是因为向量的欧式距离（L2范数）的计算方式就是“二乘”的和再开根号

PS1：距离的度量还可以用L1范数（曼哈顿距离），Lp范数（闵氏距离），L♾️范数（切比雪夫距离）来度量。

PS2: 如果你问我为什么用L2范数来度量，那么答案只能是一开始就假设了误差向量在L2空间内，自然就要用L2范数来度量。另外一种解释就是概统视角出发的，L2空间的误差e是正态分布，而基于误差e正态分布的极大似然估计就是LSE。