Repulsion Loss 遮挡场景下的目标检测

介绍

本文是旷视研究院CVPR2018上的一篇工作，在检测行人任务中，由于行人之间互相遮挡，导致传统的检测器容易受遮挡的干扰，给出错误的预测框。

研究人员先是从数据集上进行分析，定量描述了遮挡对行人检测带来的影响。后面受吸引，排斥的启发，提出了Repulsion Loss来尽可能让预测框贴近真实框的同时，又能与同类排斥，进而避免误检。

问题引入

常见的遮挡问题可以再被细分为主要两类

1. 类间遮挡，即目标被其他类遮挡住。举个例子，一个行人遛狗，人体下半部分就可能被狗狗遮住

2. 类内遮挡，目标物体被同类遮挡住，在我们问题里面也就是行人遮挡。

我们思考一下行人遮挡会对检测器造成什么影响。假设我们目标行人是T，旁边被另外一个行人B所遮挡。那么B的真实框会导致我们对T的预测框P，往B去移动(shift)，造成类似下图的情况另外我们再考虑下目标检测常用的后处理NMS，非极大值抑制。NMS操作是为了抑制去除掉多余的框。但是在行人检测中，NMS操作会带来更糟糕的检测结果。还是刚刚的例子，我对T有一个预测框P，但因为距离B靠的太近，我可能会被B的预测框给抑制，导致行人检测中出现漏检。这也从另外一个侧面反映出行人检测对NMS阈值的敏感性，阈值太低了会带来漏检，阈值太高了会带来假正例（即标出错误的目标）

因此如何稳定的检测出群体中个体行人是行人检测器的关键。

现有的方法仅仅要求预测框尽可能靠近目标框，而没有考虑周围附近的物体。受磁铁同性相斥，异性相吸的原理，我们提出了一种RepLoss新的损失函数

该损失函数在要求预测框P靠近目标框T(吸引)的同时，也要求预测框P远离其他不属于目标T的真实框(排斥)该损失函数很好的提升了行人检测模型的性能，并且降低了NMS对阈值的敏感性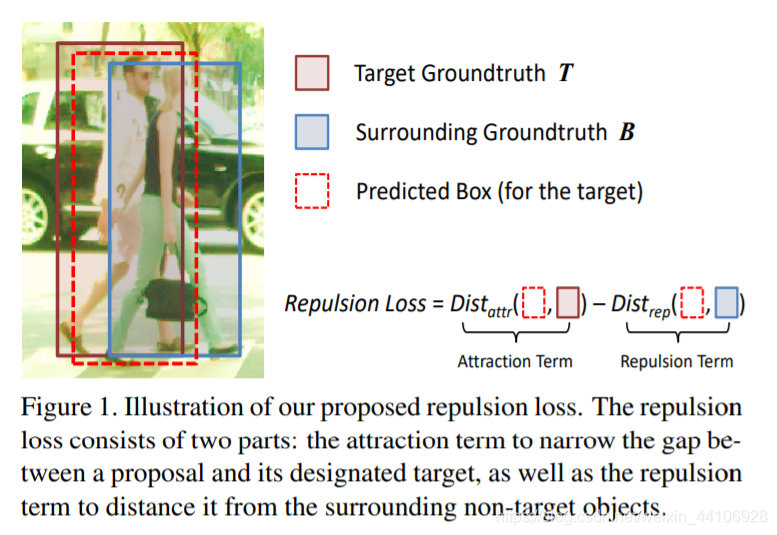

人群遮挡的影响

数据集

我们采用了CityPersons数据集，该数据集有共约35000个行人。我们的实验都基于这个数据集进行，在评价当中，我们采用log miss rate的MR−2指标来进行衡量（也就是每张图片的漏检率上取平均值，再进行log计算，该值越低越好）

检测器

我们的基线检测器沿用了Faster RCNN，将骨干网络换成resnet。由于行人检测算是小目标检测任务，因此我们给resnet增加了空洞卷积，并将下采样改为8倍（原始224->7下采样是32倍）

简单改进后的目标检测器的MR指标由15.4下降到14.6，稍微提升了点。

小目标难检测原因（补充）

1. 传统的分类网络为了减少计算量，都使用到了下采样，而下采样过多，会导致小目标的信息在最后的特征图上只有几个像素（甚至更少），信息损失较多
2. 下采样扩张的感受野比较利于大目标检测，而对于小目标，感受野可能会大于小目标本身，导致效果较差

对失败案例的分析

我们在CityPerson数据集中，由于该数据集是从分割数据集得来的，因此我们有每个行人的可见区域，即BBox_visible

为了更好分析，我们定义了一个遮挡率，如下公式

由公式可知，当行人可见区域越小，遮挡率occ越大

我们设定occ >= 0.1即为一个遮挡的案例

而occ >=0.1 并且与其他行人的IoU >=0.1，我们定义为人群遮挡案例

基于这两类设定，我们又在原数据集上划分出两个子集，分别是reasonable-occ，reasonable-crowd 很显然，reasonable-crowd也是resonable-occ的子集

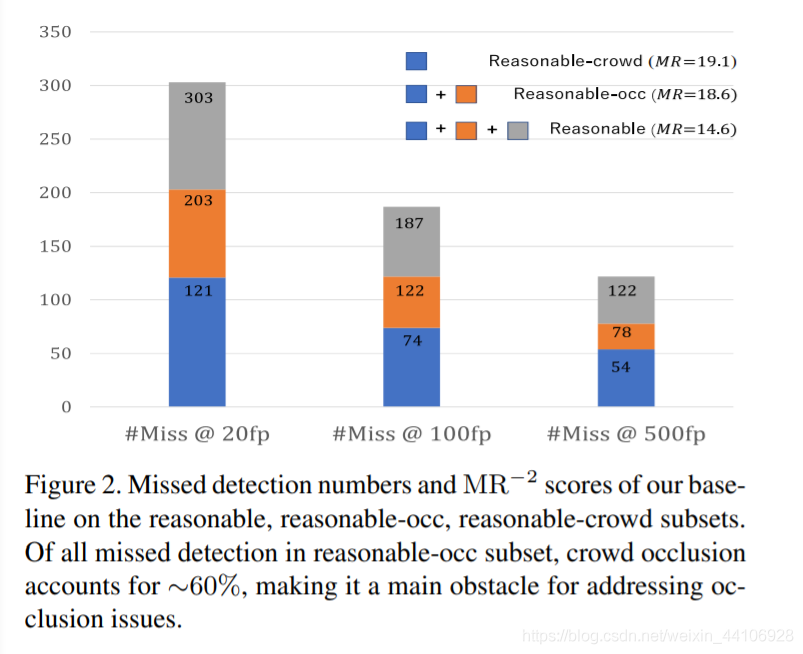蓝色，橙色，灰色分别代表Reasonable-crowd子集，Reasonable-occ子集，Reasonable集合。可以看到crowd子集在occ子集中，占据了接近60%。这也从侧面说明了人群遮挡是遮挡中一个主要问题。

假正例分析

我们同时也分析了有多少假正例是由人群遮挡造成的 我们具体分为了三类，background，localization，crowd

1. background是预测框与真实框的IoU<0.1
2. localization是预测框仅与一个真实框的IoU>=0.1
3. Crowd是预测框与多于两个真实框的IoU>=0.1

图中红框就是上述的crowd error，大约有20%的假正例都是由人群导致的 因为相邻的两个真实框，预测框或多或少产生偏移，导致预测错误

Repulsion Loss

前面分析了这么多错误，现在才是重头戏 Repulsion Loss主要由三部分构成

Lattr是为了预测框更接近真实框(即吸引)

Lrep则是为了让预测框远离周围的真实框(即排斥)

参数α和β用于平衡两者的权重

我们设 P(lP , tP , wP , hP )为候选框 G(lG, tG, wG, hG)为真实框

P+为正候选框集合，正候选框的意思是，至少与其中一个真实框的IoU大于某个阈值，这里是0.5 g = {G} 是真实框集合

Attraction term

这一项loss在其他算法也广泛使用，为了方便比较，我们沿用smoothL1 Loss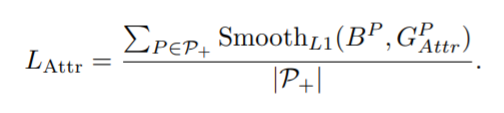

Smooth L1 Loss公式如下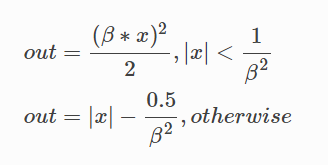这里我们的平滑系数取2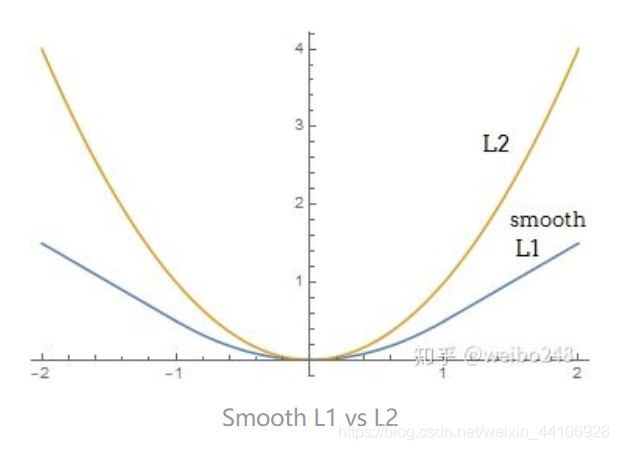

Repulsion Term (RepGT)

RepGT loss设计是为了远离非目标的真实框 对于一个候选框P，其排斥对象被定义为，除去本身要回归目标的真实框外，与其IoU最大的真实框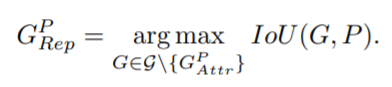受IoU loss启发，我们定义了一个IoG

损失定义如下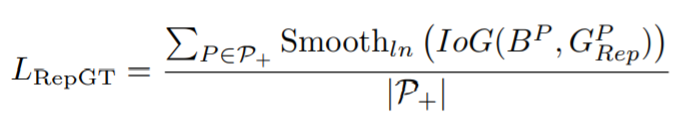这里没有采用smooth l1 loss而是smooth ln loss，其公式如下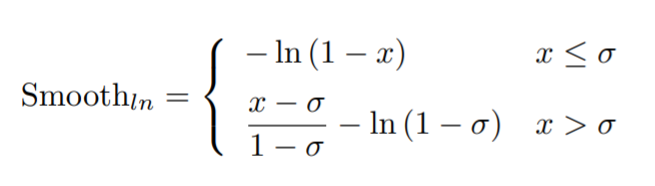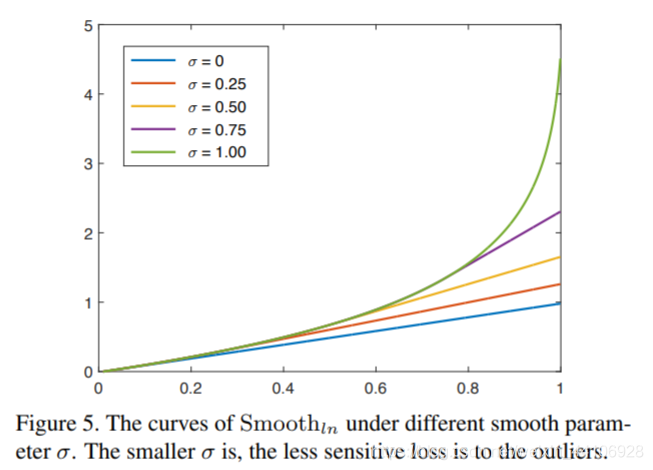不同平滑系数，最后陡峭程度不一样。当一个候选框P与非目标的真实框重叠越多，其惩罚也越大。

Repulsion Term (RepBox)

这项损失是针对人群检测中，NMS处理对阈值敏感的问题 我们先将P+集合划分成互斥的g个子集（因为一共有g个目标物体）

然后从两个不同子集随机采样，分别得到两个互斥集合的预测框，即

我们希望这两个互斥集合出来的回归框，交叉的范围尽可能小，于是有了RepBox loss，公式如下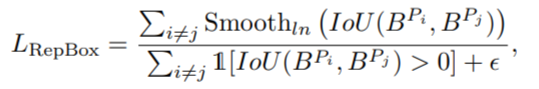其中分母的I是identity函数，即

这里限制大于0，为了避免分式除0，我们这里加了个极小值 上面依旧采用Smooth ln函数来计算。

引申讨论

距离函数选择

在惩罚项中，我们分别选择了IoG和IoU来进行度量。其原因是IoG和IoU把范围限定在了(0, 1)，与此同时 SmoothL1是无界的。如果SmoothL1用在RepGT中，它会让预测框与非目标的gt框离的越远越好，而我们的初衷只是想减少交叉部分，相比之下，IoG更符合我们的思想

另外在RepGT中使用IoG而不使用IoU的原因是，IoG的分母下，真实框大小area(G)是固定的，因此其优化目标是去减少与目标框重叠，即area(B∩G)。而在IoU下，回归器也许会尽可能让预测框更大（即分母）来最小化loss

实验部分

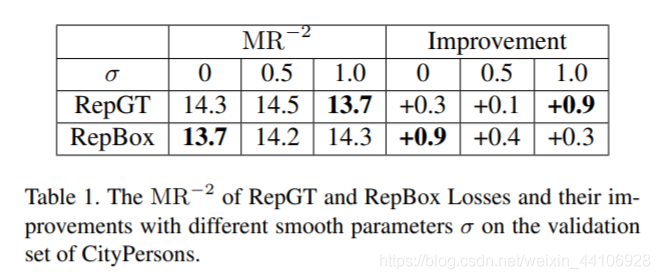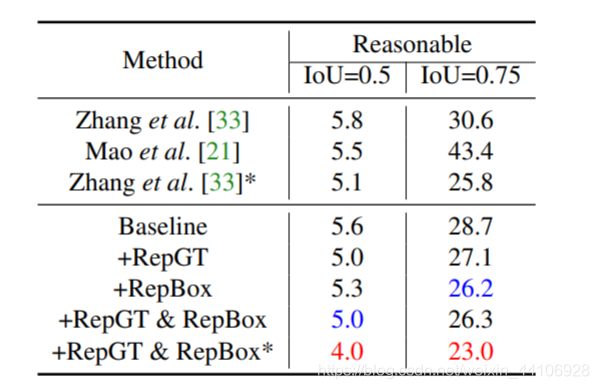
这里只简单介绍一下 我们在CityPerson和Caltech-USA分别训练了80k和160k个iter根据不同平滑系数，得到的提升也不一样 我们进一步调整两个loss的权重，相对得到了更好的效果实验效果图如下，这是未经过NMS处理的锚框图可以看到加了RepBox后，明显少了很多夹在在两个人中间的预测框，这也减少了后续NMS处理出错的情况。

代码解析

这里采用的是这版repulsion loss实现https://github.com/dongdonghy/repulsion-loss-faster-rcnn-pytorch/blob/master/lib/model/faster_rcnn/repulsion_loss.py

def IoG(box_a, box_b):                                                                                             
    inter_xmin = torch.max(box_a[0], box_b[0])                                                                     
    inter_ymin = torch.max(box_a[1], box_b[1])                                                                     
    inter_xmax = torch.min(box_a[2], box_b[2])                                                                     
    inter_ymax = torch.min(box_a[3], box_b[3])                                                                     
    Iw = torch.clamp(inter_xmax - inter_xmin, min=0)                                                               
    Ih = torch.clamp(inter_ymax - inter_ymin, min=0)                                                               
    I = Iw * Ih                                                                                                    
    G = (box_b[2] - box_b[0]) * (box_b[3] - box_b[1])                                                              
    return I / G                                                                                                   
 

该函数用于计算IoG

def repgt(pred_boxes, gt_rois, rois_inside_ws):

    sigma_repgt = 0.9
    loss_repgt=torch.zeros(pred_boxes.shape[0]).cuda()                                                                                                                                                      
    for i in range(pred_boxes.shape[0]):                                                                                                                                                                                       
        boxes = Variable(pred_boxes[i,rois_inside_ws[i]!=0].view(int(pred_boxes[i,rois_inside_ws[i]!=0].shape[0])/4,4))     
        gt = Variable(gt_rois[i,rois_inside_ws[i]!=0].view(int(gt_rois[i,rois_inside_ws[i]!=0].shape[0])/4,4))              
        num_repgt = 0
        repgt_smoothln=0
        if boxes.shape[0]>0:
            overlaps = bbox_overlaps(boxes, gt)
            for j in range(overlaps.shape[0]):
                for z in range(overlaps.shape[1]):
                    if int(torch.sum(gt[j]==gt[z]))==4:
                        overlaps[j,z]=0
            max_overlaps, argmax_overlaps = torch.max(overlaps,1)
            for j in range(max_overlaps.shape[0]):
                if max_overlaps[j]>0:
                    num_repgt+=1
                    iog = IoG(boxes[j], gt[argmax_overlaps[j]])
                    if iog>sigma_repgt:
                        repgt_smoothln+=((iog-sigma_repgt)/(1-sigma_repgt)-math.log(1-sigma_repgt))
                    elif iog<=sigma_repgt:
                        repgt_smoothln+=-math.log(1-iog)
        if num_repgt>0:
            loss_repgt[i]=repgt_smoothln/num_repgt
   
    return loss_repgt   

这是RepGT_loss代码，首先进入predbox的for循环

经过一个for循环遍历，得到除去目标真实框外，与其IoU最大的真实框

再在for循环内，通过IoG函数计算IOG值，并根据smooth ln函数（平滑系数为sigma_regpt）

最后loss总和除以repgt的个数，取得平均值

def repbox(pred_boxes, gt_rois, rois_inside_ws):

    sigma_repbox = 0
    loss_repbox=torch.zeros(pred_boxes.shape[0]).cuda()

    for i in range(pred_boxes.shape[0]):
        
        boxes = Variable(pred_boxes[i,rois_inside_ws[i]!=0].view(int(pred_boxes[i,rois_inside_ws[i]!=0].shape[0])/4,4))
        gt = Variable(gt_rois[i,rois_inside_ws[i]!=0].view(int(gt_rois[i,rois_inside_ws[i]!=0].shape[0])/4,4))
 
        num_repbox = 0
        repbox_smoothln = 0
        if boxes.shape[0]>0:
            overlaps = bbox_overlaps(boxes, boxes)
            for j in range(overlaps.shape[0]):
                for z in range(overlaps.shape[1]):
                    if z>=j:
                        overlaps[j,z]=0
                    elif int(torch.sum(gt[j]==gt[z]))==4:
                        overlaps[j,z]=0

            iou=overlaps[overlaps>0]
            for j in range(iou.shape[0]):
                num_repbox+=1
                if iou[j]<=sigma_repbox:
                    repbox_smoothln+=-math.log(1-iou[j])
                elif iou[j]>sigma_repbox:
                    repbox_smoothln+=((iou[j]-sigma_repbox)/(1-sigma_repbox)-math.log(1-sigma_repbox))

        if num_repbox>0:
            loss_repbox[i]=repbox_smoothln/num_repbox
            
    return loss_repbox

这是RepBox loss代码，第一个for循环也是进入到预测框。然后一个小for循环用来计算overlap，这里还设置一个if语句块，用来排除相同的集合（因为我们要保证两个集合是互斥的子集）。随后与RepGT类似，计算smoothln函数，最后取平均返回

总结

旷厂的这篇算法工作做的还是很扎实的，作者先是对数据集进行分析，进而根据遮挡度，拆分出两个子集，通过直观的统计来表明行人遮挡是检测行人的一大难点。然后从预测框和NMS处理上出发，找到问题所在，进而提出RepLoss，其中两项loss分别针对两个独立的问题。简单改进模型后，加上RepLoss的效果展示还是非常不错的。

欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享，坚持原创，每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧

有对文章相关的问题，或者想要加入交流群，欢迎添加BBuf微信：

为了方便读者获取资料以及我们公众号的作者发布一些Github工程的更新，我们成立了一个QQ群，二维码如下，感兴趣可以加入。