假设检验的基本步骤
假设检验属于推断统计的一种(另一种是参数估计),就是利用样本对总体进行推断。用样本量估计总体参数 μ ,先对总体参数 μ 提出假设,然后利用样本信息去检验假设是否成立。常见的 A/B Test,其背后原理就是假设检验。
举例:假设产品上要修改一个按钮颜色,按钮颜色设计为蓝色还是红色最优呢,这个判断就可以用到 A/B Test,假设有 10 W用户,随机均匀抽样 10% 的用户即 10000 人,试验组和控制组各分流 5000 人,试验组转化率为 8%,控制组转化率为 7%,试验组比控制组转化率提高 1%,那能否说明试验组比控制组更优呢,会不会是随机波动导致的?
假设检验根据样本情况、结论目的,还有很多延伸内容。本篇先来简单介绍下假设判断的基本步骤。
1. 确定原假设和备择假设
原假设也叫零假设,用 H0 表示,除非有充足证据进行反驳,否则接受这个断言。备择假设用 H1 表示,如果足够证据拒绝 H0,就接受备择假设。根据上述例子,原假设和备择假设分别为:

也就是说,如果没有显著差异,试验组转化率为 8% 并不比 控制组转化率为 7% 转化要好,可能是其他误差导致。
2. 构造检验统计量
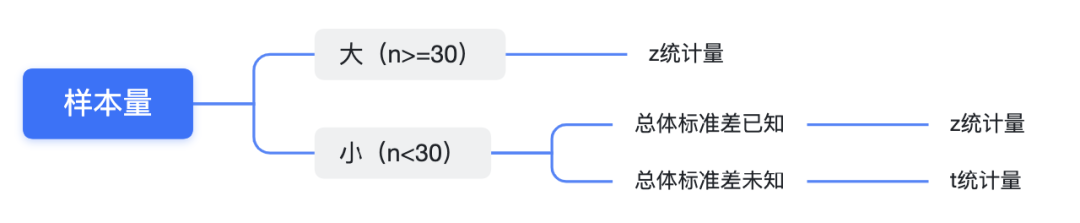
如果检验统计量服从标准正态分布,总体方差已知或样本量较大(n >= 30),检验统计量一般用 Z 表示,也称为 Z检验;如果检验统计量总体方差未知且样本容量小(n < 30),检验统计量一般用 t 表示,也称为 t 检验。
3. 确定用于做决策的显著性水平和拒绝域
显著性水平是一个概率值,希望样本结果不可信程度达到多大时就拒绝原假设 H0,通常用希腊字母 α 表示,常取值为 0.01,0.05,0.10。
根据假设的形式不同分为单尾检验和双尾检验:
单尾检验目的是比较检验统计量是否大于或者小于某个常数,因此其检验的拒绝域就放置于单侧。右侧检验拒绝域在右侧,左侧检验拒绝域在左侧。例如:中学生中男生的身高是否比女生要高;
双尾检验目的是检验统计量的均值是否有差异,拒绝域在左右两侧,例如中学生中男女身高是否有差异。
4. 计算统计检验量的P值
P 值就是当原假设为真时,P 值为某个小于或大于拒绝域方向上的一个样本结果概率。如果 P 值很小,意味着在原假设情况下,这种情况几乎不可能发生,应该拒绝原假设。
5. 作出结论
如果是左侧检验,P 值 < α,则拒绝 H0;
如果是右侧检验,P 值 > α,则拒绝 H0;
如果是双尾检验,P 值 < 1/2α,则拒绝 H0。
假设检验两类错误
第一类错误是弃真错误,原假设为真却错误的拒绝原假设,这种弃真错误称为Ⅰ型错误。其概率大小用 α 表示。
第二类错误为取伪错误,原假设为假却错误的接受了原假设,这种取伪错误称为ⅠI 型错误,其概率大小用 β 表示,β 的大小很难确切估计,α 越小,β 越大,因而可通过选定 α 控制 β 大小。
检验功效为 1-β,表示在一定检验水准下,当备择假设为真时,假设检验能够拒绝原假设的概率。
| 假设检验决策 | |||
|---|---|---|---|
| 接受H0 | 拒绝H0 | ||
| 实际情况 | H0为真 | 正确 | 第一类错误 |
| H0为假 | 第二类错误 | 正确 |
