应用算法串讲之计算复杂度优化与组合优化

大数据文摘授权转载自龙心辰
作者:龙心辰
从事算法工作以来,涉猎过不少算法。有些算法被淘汰,有些如日中天,有些则退守在某些特定的领域中顽强地生存,并不断给算法工作者提供思想启发。
自己的一个方向是算法在产业界的应用,一个很强烈的感受是即便新的算法层出不穷,真正在实践上有生命力的并不在于其思想有多炫,而是其算法特质能够最好地适应具体场景的需求。
这么多算法,什么时候用什么算法,是需要梳理清晰的。然而算法思想过于复杂,想用一两篇文章讲得面面俱到几乎不可能。
所以笔者希望用一个系列专题试图从应用的视角统一串讲一下不同算法,尽量少讲公式,着重从思想角度关注不同算法之间的横向联系和适用条件,希望对大家应用算法落地有些帮助。
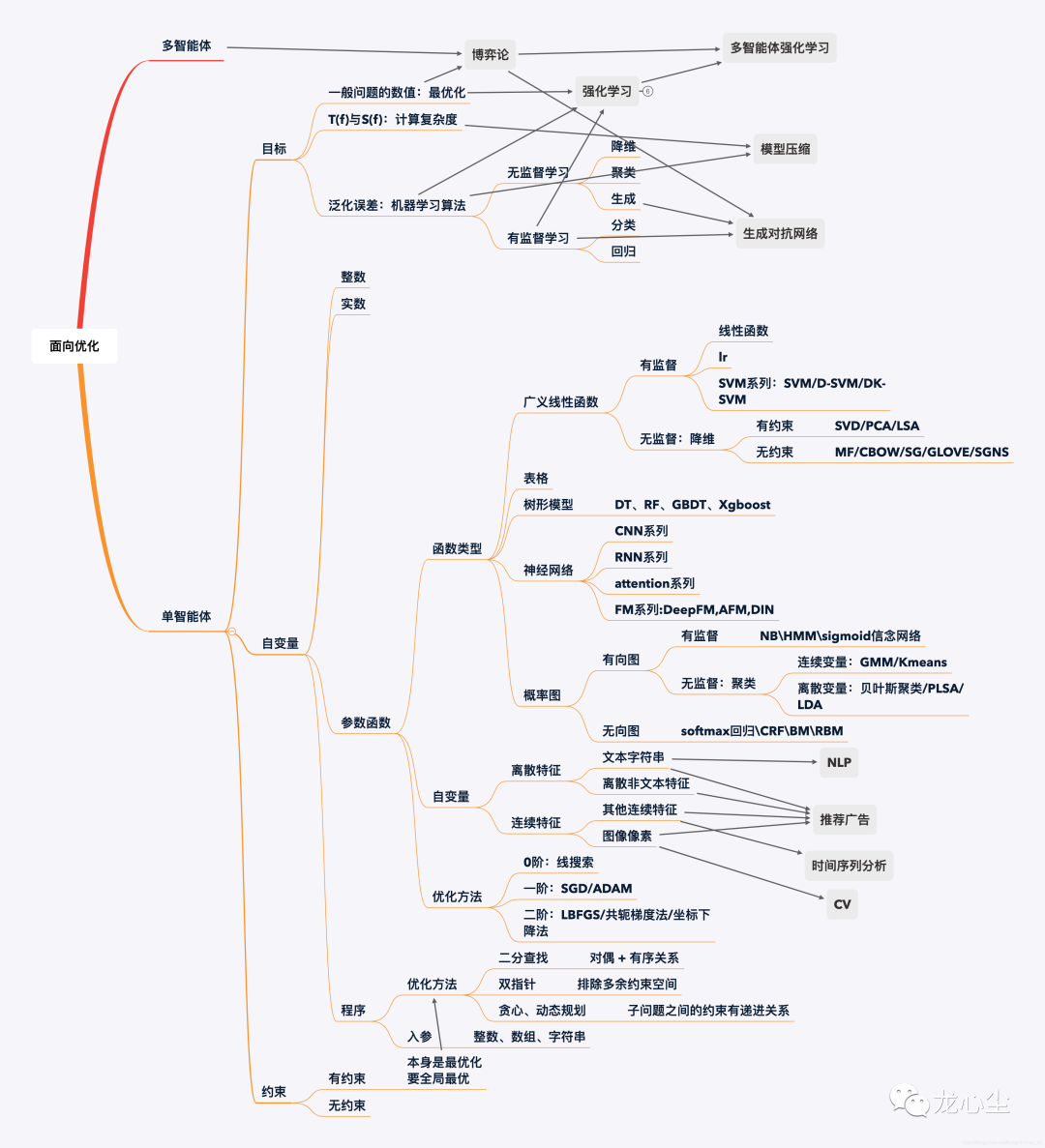
目标(因变量):F(x) 自变量(控制条件):x 约束:g(x)=0
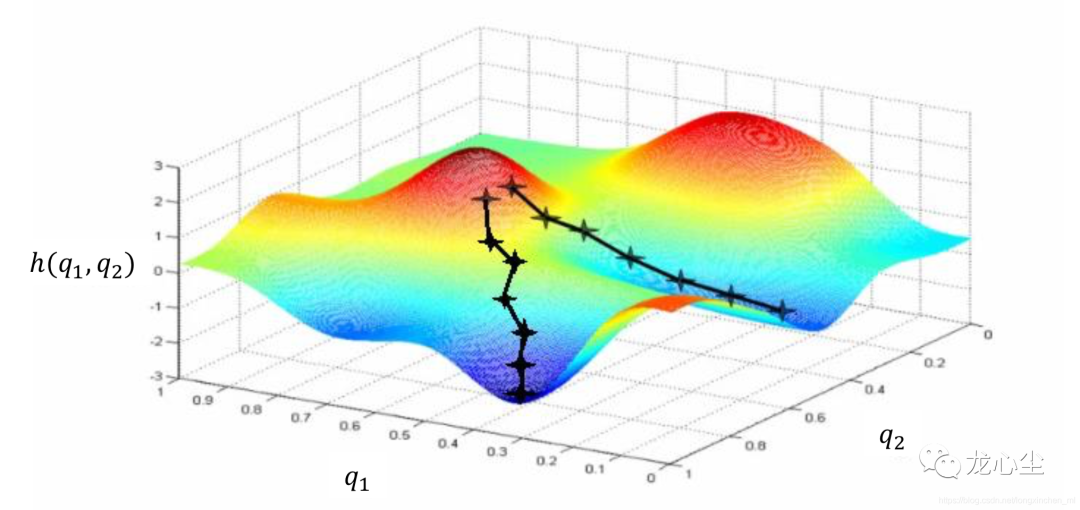
最小化目标:时间复杂度T(f)与空间复杂度S(f)
自变量:一段程序f
满足条件(约束):程序f能够实现某个特定的功能(可套娃)
这里首先要注意的是约束本身也可以是一个最优化问题,又构成了一个套娃,套娃玩出了花。

将长度为n的整数数组划分为m个片段(约束),最小化每个片段和的最大值(目标)——LeetCode1011。
在长度为n的整数数组中,找出一个的和大于等于s的连续子数组(约束),最小化子数组的长度(目标)——LeetCode209。
在长度为n的整数数组中,找出一个递增子序列(约束),最大化子序列的长度(目标)——LeetCode300。
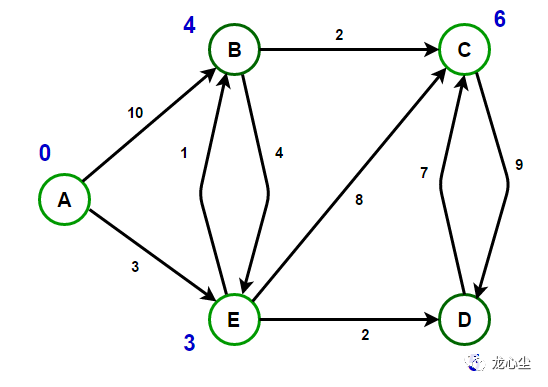
最小化目标(程序出参):所有划分片段的子数组和的最大值。
自变量(程序入参):长度为n的整数数组,整数m。
约束(程序必需满足逻辑):将整数数组划分为m个子片段。
回过头来看外层套娃的最优化问题,其目的就是找出一个最佳的可执行的程序。而这个是需要人手动写出来的。那有没有能够自动化编程的算法呢?

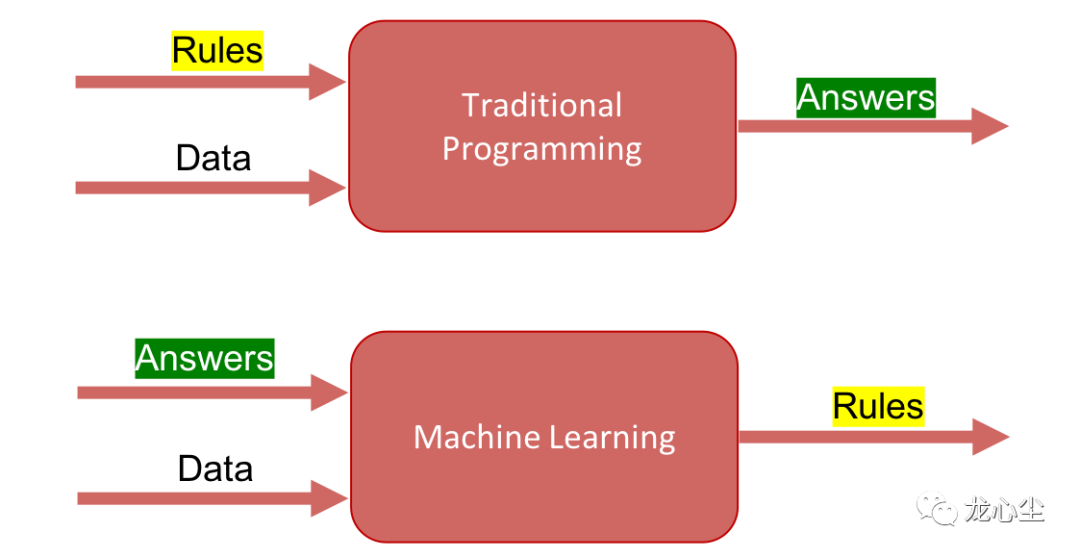

评论
